Chapter 8, Problem 44E

(a)

To determine

To make a scatterplot and describe the general trend in birth rates.

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. Thus, the scatterplot is as follows:

  

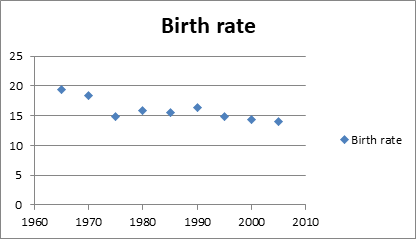
In the above scatterplot, the birth rates are on the vertical line and the years are on the horizontal line. By the scatterplot we can see that the as the years increases the birth rates of women decreases. So, we can see that the relationship is negative in nature and as the points are less scattered so, the relationship can be strong and linear.

(b)

To determine

To find the equation of the regression line.

Answer to Problem 44E

  $\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=234.32-0.110(\text{Years)}$ .

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. Thus, we have the table as:

Year	Birth rate
1965	19.4
1970	18.4
1975	14.8
1980	15.9
1985	15.6
1990	16.4
1995	14.8
2000	14.4
2005	14

Thus, we will calculate the mean and standard deviation of the age and price by using excel as,

Formula used:

The formula for mean is as:

  $\text{AVERAGE}\left(\text{number1,}\left[\text{number2}\right]\text{, }\mathrm{...}\right)$

And the formula for the standard deviation is as:

  $\text{STDEV}\left(\text{number1,}\left[\text{number2}\right]\text{,}\mathrm{...}\right]\text{)}$

And the formula for correlation is:

  $\text{Correl(array1,array2)}$

Calculation:

The mean, standard deviation and correlation is calculated as:

For the mean,

	Year	Birth rate
Average =	=AVERAGE(D46:D54)	=AVERAGE(E46:E54)

For the standard deviation,

	Year	Birth rate
Standard deviation =	=STDEV(D46:D54)	=STDEV(E46:E54)

For the correlation,

Correlation

=CORREL(D46:D54,E46:E54)

And the result is as:

For the mean,

	Year	Birth rate
Average =	1985	15.97

For the standard deviation,

	Year	Birth rate
Standard deviation =	13.69	1.84

For the correlation,

Correlation =

-0.821

So, we have,

  $\begin{array}{l}r=-0.821\\ {\mu }_1=15.97\\ {\mu }_2=1985\\ {\sigma }_1=1.84\\ {\sigma }_2=13.69\end{array}$

Thus, the equation of the regression line can be calculated as:

  $\begin{array}{l}\beta =r\times \frac{{\sigma }_1}{{\sigma }_2}\\ =-0.821\times \frac{1.84}{13.69}\\ =-0.110\\ \alpha ={\mu }_1-\beta \times {\mu }_2\\ =15.97+0.110\times 1985\\ =234.32\end{array}$

And the regression equation is as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=\alpha +\beta (\text{Years)}\\ =234.32-0.110(\text{Years)}\end{array}$

(c)

To determine

To check to see if the line is an appropriate model.

Answer to Problem 44E

The model is appropriate.

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. So, we have,

  $\begin{array}{l}r=-0.821\\ {\mu }_1=15.97\\ {\mu }_2=1985\\ {\sigma }_1=1.84\\ {\sigma }_2=13.69\end{array}$

And the regression equation is as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=\alpha +\beta (\text{Years)}\\ =234.32-0.110(\text{Years)}\end{array}$

To check if the line is an appropriate model, we will check the residual plot of this model. Thus, we see that the residual plot does not show a visible pattern then this linear model is appropriate.

(d)

To determine

To interpret the slope of the line.

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. So, we have,

  $\begin{array}{l}r=-0.821\\ {\mu }_1=15.97\\ {\mu }_2=1985\\ {\sigma }_1=1.84\\ {\sigma }_2=13.69\end{array}$

And the regression equation is as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=\alpha +\beta (\text{Years)}\\ =234.32-0.110(\text{Years)}\end{array}$

Thus, the slope of the line interprets that on average, every year the birth rates per $1000$ women in the United States is decreased by $0.110$ .

(e)

To determine

To estimate what the rate was in $1978$ .

Answer to Problem 44E

The rate was $17.40$ in $1978$ .

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. So, we have,

  $\begin{array}{l}r=-0.821\\ {\mu }_1=15.97\\ {\mu }_2=1985\\ {\sigma }_1=1.84\\ {\sigma }_2=13.69\end{array}$

And the regression equation is as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=\alpha +\beta (\text{Years)}\\ =234.32-0.110(\text{Years)}\end{array}$

Thus, the birth rate in the year $1978$ is calculated as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=234.32-0.110(\text{Years)}\\ =234.32-0.110\times 1978\\ =17.40\end{array}$

(f)

To determine

To find out how close did your model come.

Answer to Problem 44E

Our model is just $2.4$ rate far away from the actual rate.

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. So, we have,

  $\begin{array}{l}r=-0.821\\ {\mu }_1=15.97\\ {\mu }_2=1985\\ {\sigma }_1=1.84\\ {\sigma }_2=13.69\end{array}$

And the regression equation is as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=\alpha +\beta (\text{Years)}\\ =234.32-0.110(\text{Years)}\end{array}$

It is given that the actual rate in $1978$ was $15$ but in the part (e) the predicted rate was $17.40$ , thus the difference is as:

  $\begin{array}{l}=\text{Actual}-\text{ Predicted}\\ =15-17.40\\ =-2.4\end{array}$

Thus, our model is just $2.4$ rate far away from the actual rate.

(g)

To determine

To predict what the birth rate will be in $2010$ and comment on your faith in this prediction.

Answer to Problem 44E

The birth rate that will be in $2010$ is $13.22$ .

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. So, we have,

  $\begin{array}{l}r=-0.821\\ {\mu }_1=15.97\\ {\mu }_2=1985\\ {\sigma }_1=1.84\\ {\sigma }_2=13.69\end{array}$

And the regression equation is as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=\alpha +\beta (\text{Years)}\\ =234.32-0.110(\text{Years)}\end{array}$

Thus, the birth rate that will be in year $2010$ can be calculated as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=234.32-0.110(\text{Years)}\\ =234.32-0.110\times 2010\\ =13.22\end{array}$

We can say about the faith in this prediction that as the year will increase in the future this model will be less appropriate because we cannot say about the trend that will be occurring in the future about the birth rates as it can increase due to future innovations and technologies.

(h)

To determine

To predict what the birth rate will be in $2025$ and comment on your faith in this prediction.

Answer to Problem 44E

The birth rate that will be in $2025$ is $11.57$ .

Explanation of Solution

In the equation it is given the information about the number of lives of women during the years in the United States. So, we have,

  $\begin{array}{l}r=-0.821\\ {\mu }_1=15.97\\ {\mu }_2=1985\\ {\sigma }_1=1.84\\ {\sigma }_2=13.69\end{array}$

And the regression equation is as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=\alpha +\beta (\text{Years)}\\ =234.32-0.110(\text{Years)}\end{array}$

Thus, the birth rate that will be in year $2025$ can be calculated as:

  $\begin{array}{l}\text{<mover accent="true"><mo>B</mo><mo>^</mo></mover> irth rates}=234.32-0.110(\text{Years)}\\ =234.32-0.110\times 2025\\ =11.57\end{array}$

We can say about the faith in this prediction that as the year will increase in the future this model will be less appropriate because we cannot say about the trend that will be occurring in the future about the birth rates as it can increase due to future innovations and technologies.