Chapter 7.6, Problem 97AYU

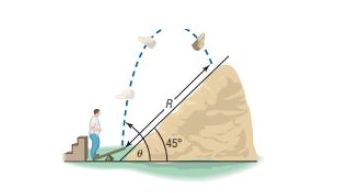
Projectile Motion An object is propelled upward at an angle $\theta ,{\text{ 45}}^{\circ }\text{ < }\theta {\text{ < 90}}^{\circ }$, to the horizontal with an initial velocity $v_0$ feet per second from the base of a plane that makes an angle of ${45}^{\circ }$ with the horizontal. See the illustration. If air resistance is ignored, the distance $R$ that it travels up the inclined plane is given by the function

$R\left(\theta \right)\text{ = }\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right)$

Show that

$R\left(\theta \right)\text{ = }\frac{v_0^2\sqrt{2}}{32}[sin\left(2\theta \right)-cos\left(2\theta \right)-1]$

In calculus, you will be asked to find the angle $\theta$ that maximizes $R$ by solving the equation

$\sin \left(2\theta \right)\text{ + cos}\left(2\theta \right)\text{ = 0}$

solve the equation for $\theta$.

What is the maximum distance $R$ if $v_0\text{ =32}$ feet per second?

Graph $R\text{ = }R\left(\theta \right),{\text{ 45}}^{\circ }\le \theta \le {\text{ 90}}^{\circ }$, and find the angle $\theta$ that maximizes the distance $R$. Also find the maximum distance. Use $v_0\text{ = 32 }$ feet per second. Compare the results with the answers found in parts (b) and (c).

To determine

To show:

a. $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{32}\left(\sin 2\theta -\cos 2\theta -1\right)$

Answer to Problem 97AYU

a. $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{32}\left(\sin 2\theta -\cos 2\theta -1\right)$

Explanation of Solution

Given:

An object is propelled upward at an angle $\theta$, ${45}^{\circ }<\theta <{90}^{\circ }$, to the horizontal with an initial velocity of $v_0$ feet per second from the base of a plane that makes an angle of ${45}^{\circ }$ with the horizontal. See the illustration. If air resistance is ignored, the distance $R$ that it travels up the inclined plane is given by the function $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right)$.

Calculation:

a. $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right)$

$R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{16}\left(\cos \theta \sin \theta -{\cos }^2\theta \right)$

$R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{16}\left(\frac{\sin 2\theta }{2}-\left(\frac{1+\cos 2\theta }{2}\right)\right)$

$R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{32}\left(\sin 2\theta -\cos 2\theta -1\right)$

To determine

To show:

b. In calculus, you will be asked to find the angle $\theta$ that maximizes $R$ by solving the equation $\sin 2\theta +\cos 2\theta =0$. Solve this equation for $\theta$.

Answer to Problem 97AYU

b. $\frac{3\pi }{8}$

Explanation of Solution

Given:

An object is propelled upward at an angle $\theta$, ${45}^{\circ }<\theta <{90}^{\circ }$, to the horizontal with an initial velocity of $v_0$ feet per second from the base of a plane that makes an angle of ${45}^{\circ }$ with the horizontal. See the illustration. If air resistance is ignored, the distance $R$ that it travels up the inclined plane is given by the function $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right)$.

Calculation:

b. $\sin 2\theta +\cos 2\theta =0$

$\sin 2\theta =-\cos 2\theta$

$\frac{\sin 2\theta }{\cos 2\theta }=-1$

$\tan 2\theta =-1$

$2\theta ={\tan }^{-1}\left(-1\right)$

$\theta =\frac{1}{2}\left(\frac{3\pi }{4}\right)$

$=\frac{3\pi }{8}$

To determine

To show:

c. What is the maximum distance $R$ if $v_0=32$ feet per second?

Answer to Problem 97AYU

c. $32\left(2-\sqrt{2}\right)$

Explanation of Solution

Given:

An object is propelled upward at an angle $\theta$, ${45}^{\circ }<\theta <{90}^{\circ }$, to the horizontal with an initial velocity of $v_0$ feet per second from the base of a plane that makes an angle of ${45}^{\circ }$ with the horizontal. See the illustration. If air resistance is ignored, the distance $R$ that it travels up the inclined plane is given by the function $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right)$.

Calculation:

c. $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{32}\left(\sin 2\theta -\cos 2\theta -1\right)$

$R\left(\frac{3\pi }{8}\right)=\frac{{32}^2\sqrt{2}}{32}\left(\sin \frac{3\pi }{8}-\cos \frac{3\pi }{8}-1\right)$

$=32\sqrt{2}\left(\sin {90}^{\circ }-\cos {90}^{\circ }-1\right)$

$=32\sqrt{2}\left(\sqrt{2}-1\right)$

$=32\left(2-\sqrt{2}\right)$

To determine

To show:

d. Graph $R=R\left(\theta \right),{45}^{\circ }\le \theta \le {90}^{\circ }$, and find the angle $\theta$ that maximizes the distance $R$. Also find the maximum distance. Use $v_0=32$ feet per second. Compare the results with the answers found in parts (b) and (c).

Answer to Problem 97AYU

d.

Explanation of Solution

Given:

An object is propelled upward at an angle $\theta$, ${45}^{\circ }<\theta <{90}^{\circ }$, to the horizontal with an initial velocity of $v_0$ feet per second from the base of a plane that makes an angle of ${45}^{\circ }$ with the horizontal. See the illustration. If air resistance is ignored, the distance $R$ that it travels up the inclined plane is given by the function $R\left(\theta \right)=\frac{v_0^2\sqrt{2}}{16}\cos \theta \left(\sin \theta -\cos \theta \right)$.

Calculation:

d.