Chapter 7.6, Problem 33WE

To determine

To Prove : The Ceva's Theorem for the given conditions.

Explanation of Solution

Given information:

If P is any point inside $\text{Δ}ABC,\text{then}\frac{AX}{XB}\cdot \frac{BY}{YC}\cdot \frac{CZ}{ZA}=1$ .

  

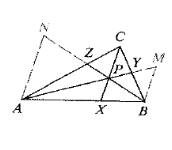
Construct ?ABC with points Y, Z, and X on sides BC, AC, and AB, respectively.

Let the concurrent line segments be AY, BZ and CX.

The point of intersection is point P.

Construct line I through C parallel to line AB and extend segments AY and BZ to meet I at points G and H, respectively.

  

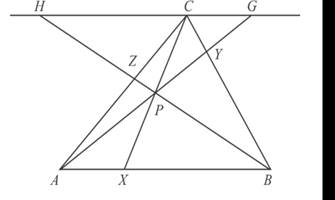
Since $l$ and AB are parallel, angle $\Delta ABC$ congruent to $\Delta CHZ$ ,

Since they are alternate interior angles with respect to the transversal BH

Similarly $\Delta BAZ$ congruent to $\Delta HCZ$ , since they are alternate interior angles with respect to the transversal AC

Hence, triangles $\Delta ABC$ and $\Delta CHZ$ are similar.

By the same reasoning, the following pairs of similar triangles

  $\begin{array}{l}\text{Δ}ABZ\sim \text{Δ}CHZ\hfill \\ \text{Δ}APX\sim \text{Δ}GPC\hfill \\ \text{Δ}BPX\sim \text{Δ}HPC\hfill \\ \text{Δ}GYC\sim \text{Δ}AYB\hfill \end{array}$

From the first similarity,

  $\frac{AZ}{CZ}=\frac{AB}{CH}\dots \dots$

  $\begin{array}{l}\frac{BX}{AX}=\frac{BX}{OX}\cdot \frac{OX}{AX}=\frac{CH}{PC}\cdot \frac{PC}{CG}\dots \dots (2)\\ =\frac{CH}{CG}\\ \text{From the fourth similarity,}\\ \frac{CY}{BY}=\frac{CG}{AB}\dots \dots (3)\\ \text{Then,using the equations (1), (2), and (3)},\\ \frac{AZ}{CZ}\cdot \frac{CY}{BY}\cdot \frac{BX}{AX}=\frac{AB}{CH}\cdot \frac{CG}{AB}\cdot \frac{CH}{CG}=1\end{array}$

Hence. Ceva's theorem is proved.