Chapter 7, Problem 96P

To determine

(a)

The dimensional parameter generated by the given quantities.

Explanation of Solution

Given information:

$\begin{array}{l}\text{force}\text{pressure}\text{gradient}\text{=}\frac{\text{dP}}{\text{dx}}\\ \text{Flow}\text{}\text{:}\text{steady+}\text{}\text{incomprssible}\\ \text{down}\text{stream}\text{distance}\text{=}\text{x}\\ \text{component}\text{of}\text{velocity}\text{in}\text{x-direction}\text{=}\text{u}\\ \text{distance}\text{=}\text{h}\\ \text{fluid}\text{viscosity}\text{=}\text{μ}\\ \text{vertical}\text{coordinate}\text{=}\text{y}\end{array}$

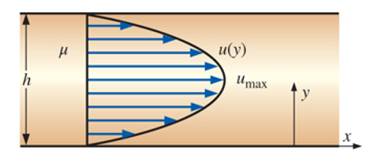
In the given question,

We use the method of variable to find the dimensionless quantity from the given data.

Total number of parameters given,

n = 5

We define the function as,

Primary dimensions of all the given parameters,

$\begin{array}{l}\text{1}\text{.}\\ \text{u}\text{=}\text{component}\text{of}\text{velocity}\text{in}\text{x-direction}\\ \left\{\text{u}\right\}\text{=}\left\{\text{velocity}\right\}\\ \left\{\text{u}\right\}\text{=}\left\{\frac{\text{L}}{\text{t}}\right\}\\ \left\{\text{u}\right\}\text{=}\left\{{\text{L}}^{\text{1}}{\text{t}}^{\text{-1}}\right\}\end{array}$

$\begin{array}{l}\text{2}\text{.}\\ \text{h}=\text{distance}\\ \left\{\text{h}\right\}\text{=}\left\{\text{distance}\right\}\\ \left\{\text{h}\right\}\text{=}\left\{\text{L}\right\}\end{array}$

$\begin{array}{l}\text{3}\text{.}\\ \frac{\text{dP}}{\text{dx}}\text{=}\text{force}\text{pressure}\text{gradient}\\ \left\{\frac{\text{dP}}{\text{dx}}\right\}\text{=}\left\{\frac{\text{pressure}}{\text{distance}}\right\}\\ \left\{\frac{\text{dP}}{\text{dx}}\right\}\text{=}\left\{\frac{{\text{ML}}^{\text{-1}}{\text{t}}^{\text{-2}}}{\text{distance}}\right\}\\ \left\{\frac{\text{dP}}{\text{dx}}\right\}\text{=}\left\{\frac{{\text{ML}}^{\text{-1}}{\text{t}}^{\text{-2}}}{\text{L}}\right\}\\ \left\{\frac{\text{dP}}{\text{dx}}\right\}\text{=}\left\{{\text{ML}}^{\text{-2}}{\text{t}}^{\text{-2}}\right\}\end{array}$

$\begin{array}{l}\text{4}\text{.}\\ \text{μ}\text{=}\text{fluid}\text{viscosity}\\ \left\{\text{μ}\right\}\text{=}\left\{\frac{\text{mass}}{\text{length}\text{×}\text{time}}\right\}\\ \left\{\text{μ}\right\}\text{=}\left\{\frac{\text{M}}{\text{L}\text{×}\text{t}}\right\}\\ \left\{\text{μ}\right\}\text{=}\left\{\frac{\text{M}}{\text{Lt}}\right\}\\ \left\{\text{μ}\right\}\text{=}\left\{{\text{ML}}^{\text{-1}}{\text{t}}^{\text{-1}}\right\}\end{array}$

$\begin{array}{l}\text{5}\text{.}\\ \text{y}\text{=}\text{vertical}\text{coordinate}\\ \left\{\text{y}\right\}\text{=}\left\{\text{vertical}\text{coordinate}\right\}\\ \left\{\text{y}\right\}\text{=}\left\{\text{L}\right\}\\ \left\{\text{y}\right\}\text{=}\left\{{\text{L}}^1\right\}\end{array}$

The number of primary dimensions is (L, M, t).

Since the value of n is 5.

So,

J = 3,

And,

k = (N − J)

k = (5 − 3) = 2.

So, the number of pi-terms is two.

For further calculation we need to choose any three repeating quantities,

I choose $\left(h,\frac{\text{dP}}{\text{dx}},\text{μ}\right)$.

Thus, by using repeating variables, first independent pi- term is formed.

$\begin{array}{l}\text{1}\text{.}\text{First}\text{pi-term,}\\ \left\{{\text{π}}_{\text{1}}\right\}\text{=}\left\{\left(\text{u}\right){\left(\text{h}\right)}^{{\text{a}}_{\text{1}}}{\left({\text{ML}}^{\text{-2}}{\text{t}}^{\text{-2}}\right)}^{{\text{b}}_{\text{1}}}{\left({\text{ML}}^{\text{-1}}{\text{t}}^{\text{-1}}\right)}^{{\text{c}}_{\text{1}}}\right\}\\ \left\{{\text{π}}_{\text{1}}\right\}\text{=}\left\{\left(\text{u}\right){\left(\text{h}\right)}^{{\text{a}}_{\text{1}}}{\left({\text{ML}}^{\text{-2}}{\text{t}}^{\text{-2}}\right)}^{{\text{b}}_{\text{1}}}{\left({\text{ML}}^{\text{-1}}{\text{t}}^{\text{-1}}\right)}^{{\text{c}}_{\text{1}}}\right\}\\ \text{mass}\text{:}\\ \left\{{\text{m}}^{\text{0}}\right\}\text{=}{\text{m}}^{{\text{b}}_{\text{1}}}{\text{m}}^{{\text{c}}_{\text{1}}}\\ \text{0=}{\text{b}}_{\text{1}}\text{+}{\text{c}}_{\text{1}}\Rightarrow {\text{c}}_{\text{1}}\text{=}{\text{-b}}_{\text{1}}\end{array}$

$\begin{array}{l}\text{time}\text{:}\\ \left\{{\text{t}}^{\text{0}}\right\}\text{=}\left\{{\text{t}}^{\text{-1}}{\text{t}}^{{\text{-2b}}_{\text{1}}}{\text{t}}^{{\text{-c}}_{\text{1}}}\right\}\\ \text{0}\text{=}{\text{-1-2b}}_{\text{1}}\text{-}{\text{c}}_{\text{1}}\\ \Rightarrow \text{0}\text{=}{\text{-1-2b}}_{\text{1}}\text{-}\left({\text{-b}}_{\text{1}}\right)\\ \Rightarrow \text{0}\text{=}{\text{-1-2b}}_{\text{1}}\text{+}{\text{b}}_{\text{1}}\\ \Rightarrow \text{0}\text{=}\text{-1-}{\text{b}}_{\text{1}}\\ \Rightarrow \boxed{{\text{b}}_{\text{1}}\text{=}\text{-1}}\\ \text{So, }\\ \boxed{\therefore {\text{c}}_{\text{1}}\text{=}\text{1}}\end{array}$

$\begin{array}{l}\text{length:}\\ \left\{{\text{L}}^{\text{0}}\right\}\text{=}\left\{{\text{L}}^{\text{1}}{\text{L}}^{{\text{a}}_{\text{1}}}{\text{L}}^{{\text{-2b}}_{\text{1}}}{\text{L}}^{{\text{-c}}_{\text{1}}}\right\}\\ \text{0}\text{=}{\text{1+a}}_1{\text{-2b}}_{\text{1}}\text{-}{\text{c}}_{\text{1}}\\ \Rightarrow \text{0}\text{=}{\text{1+a}}_1{\text{-2b}}_{\text{1}}\text{-}{\text{c}}_{\text{1}}\\ \Rightarrow \text{0}\text{=}{\text{1+a}}_1\text{-2}\left(\text{-1}\right)\text{-}\left(1\right)\\ \Rightarrow \text{0}\text{=}{\text{a}}_1+\text{2}\\ \Rightarrow \boxed{{\text{a}}_{\text{1}}\text{=}\text{-2}}\end{array}$

So, the substituting the values of variables to get a dimensionless relationship. ${\text{u}}_{\max }$ is s velocity component. The dimension of u and ${\text{u}}_{\max }$ will remain same.

Thus, the required relationship is,

$\boxed{{\text{π}}_{\text{1}}\text{=}\frac{\mu {\text{u}}_{\max }}{{\text{h}}^{\text{2}}\frac{\text{dP}}{\text{dx}}}=\text{constant}\text{=}\text{C}}\mathrm{....}\text{(i)}$

On simplifying,

$\boxed{{\text{u}}_{\max }\text{=}\text{C}\frac{{\text{h}}^{\text{2}}}{\mu }\frac{\text{dP}}{\text{dx}}}\mathrm{...}\left(2\right)$

To determine

(b)

The change in ${\text{u}}_{\max }$ when h is doubled.

Answer to Problem 96P

${\text{u}}_{\max }$ becomes 4-times

$\boxed{{\text{u}}_{\max ,2h}\text{=}\left(4\right){\text{u}}_{\max }}$

Explanation of Solution

Given information:

$\begin{array}{l}\text{force}\text{pressure}\text{gradient}\text{=}\frac{\text{dP}}{\text{dx}}\\ \text{Flow}\text{}\text{:}\text{steady+}\text{}\text{incomprssible}\\ \text{down}\text{stream}\text{distance}\text{=}\text{x}\\ \text{component}\text{of}\text{velocity}\text{in}\text{x-direction}\text{=}\text{u}\\ \text{distance}\text{=}\text{h}\\ \text{fluid}\text{viscosity}\text{=}\text{μ}\\ \text{vertical}\text{coordinate}\text{=}\text{y}\end{array}$

From subpart a,

$\boxed{{\text{π}}_{\text{1}}\text{=}\frac{\mu {\text{u}}_{\max }}{{\text{h}}^{\text{2}}\frac{\text{dP}}{\text{dx}}}=\text{constant}\text{=}\text{C}}\mathrm{....}\text{(i)}$

On simplifying,

$\boxed{{\text{u}}_{\max }\text{=}\text{C}\frac{{\text{h}}^{\text{2}}}{\mu }\frac{\text{dP}}{\text{dx}}}\mathrm{...}\left(2\right)$

When h is doubled,

$\begin{array}{l}{\text{u}}_{\max ,2h}\text{=}\text{C}\frac{{\left(2\text{h}\right)}^{\text{2}}}{\mu }\frac{\text{dP}}{\text{dx}}\\ {\text{u}}_{\max ,2h}\text{=}\left(4\right)\text{C}\frac{{\text{h}}^{\text{2}}}{\mu }\frac{\text{dP}}{\text{dx}}\\ {\text{u}}_{\max ,2h}\text{=}\left(4\right){\text{u}}_{\max }\end{array}$

To determine

(c)

The change in ${\text{u}}_{\max }$ when $\frac{\text{dP}}{\text{dx}}$ is doubled.

Answer to Problem 96P

${\text{u}}_{\max }$ becomes 4-times

$\boxed{{\text{u}}_{\max ,2h}\text{=}\left(4\right){\text{u}}_{\max }}$

Explanation of Solution

Given information:

$\begin{array}{l}\text{force}\text{pressure}\text{gradient}\text{=}\frac{\text{dP}}{\text{dx}}\\ \text{Flow}\text{}\text{:}\text{steady+}\text{}\text{incomprssible}\\ \text{down}\text{stream}\text{distance}\text{=}\text{x}\\ \text{component}\text{of}\text{velocity}\text{in}\text{x-direction}\text{=}\text{u}\\ \text{distance}\text{=}\text{h}\\ \text{fluid}\text{viscosity}\text{=}\text{μ}\\ \text{vertical}\text{coordinate}\text{=}\text{y}\end{array}$

From subpart a,

$\boxed{{\text{π}}_{\text{1}}\text{=}\frac{\mu {\text{u}}_{\max }}{{\text{h}}^{\text{2}}\frac{\text{dP}}{\text{dx}}}=\text{constant}\text{=}\text{C}}\mathrm{....}\text{(i)}$

On simplifying,

$\boxed{{\text{u}}_{\max }\text{=}\text{C}\frac{{\text{h}}^{\text{2}}}{\mu }\frac{\text{dP}}{\text{dx}}}\mathrm{...}\left(2\right)$

When $\frac{\text{dP}}{\text{dx}}$ is doubled,

$\begin{array}{l}{\text{u}}_{\max }\text{=}\text{C}\frac{{\text{h}}^{\text{2}}}{\mu }\frac{\text{dP}}{\text{dx}}\\ {\text{u}}_{\max ,2\frac{\text{dP}}{\text{dx}}}\text{=}\text{C}\frac{{\text{h}}^{\text{2}}}{\mu }\left(2\right)\frac{\text{dP}}{\text{dx}}\\ {\text{u}}_{\max ,2\frac{\text{dP}}{\text{dx}}}\text{=}\left(2\right)\text{C}\frac{{\text{h}}^{\text{2}}}{\mu }\frac{\text{dP}}{\text{dx}}\end{array}$

$\boxed{{\text{u}}_{\max ,2\frac{\text{dP}}{\text{dx}}}\text{=}\left(2\right){\text{u}}_{\max }}$

To determine

(d)

The number of experiments required to describe complete relationship.

Answer to Problem 96P

The number of experiments required is 2.

Explanation of Solution

Given information:

$\begin{array}{l}\text{force}\text{pressure}\text{gradient}\text{=}\frac{\text{dP}}{\text{dx}}\\ \text{Flow}\text{}\text{:}\text{steady+}\text{}\text{incomprssible}\\ \text{down}\text{stream}\text{distance}\text{=}\text{x}\\ \text{component}\text{of}\text{velocity}\text{in}\text{x-direction}\text{=}\text{u}\\ \text{distance}\text{=}\text{h}\\ \text{fluid}\text{viscosity}\text{=}\text{μ}\\ \text{vertical}\text{coordinate}\text{=}\text{y}\end{array}$

From previous problem,

$\boxed{{\text{π}}_{\text{1}}\text{=}\frac{\mu {\text{u}}_{\max }}{{\text{h}}^{\text{2}}\frac{\text{dP}}{\text{dx}}}=\text{f}\left(\frac{\text{y}}{\text{h}}\right)}$

${\text{π}}_{\text{1}}\text{=}\frac{\mu {\text{u}}_{\max }}{{\text{h}}^{\text{2}}\frac{\text{dP}}{\text{dx}}}$

$\boxed{{\text{π}}_2\text{=}\frac{\text{y}}{\text{h}}}$

There exist two pi-terms in the given question,

So, we need to perform two experiment for generation complete relationship between the given parameters.