Chapter 7, Problem 7.1P

Consider the following fluids at a film temperature of 300 K in parallel flow over a flat plate with velocity of 1 m/s: atmospheric air, water, engine oil, and mercury.

1. For each fluid, determine the velocity and thermal boundary layer thicknesses at a distance of 40 mm from the leading edge.
2. For each of the prescribed fluids and on the same coordinates, plot the boundary layer thicknesses as a function of distance from the leading edge to a plate length of 40 mm.

To determine

The velocity and thermal boundary layer thickness at a distance of $40\text{mm}$ from the leading edge.

Answer to Problem 7.1P

The thermal boundary layer thickness for air, water, oil and mercury is 4.48, 0.52, 1.27, and 1.17 respectively.

Explanation of Solution

Given Information:

Properties of air at $300\text{K}\text{, 1}\text{atm}$ .

  $v=15.89\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ , $\mathrm{Pr}=0.707$ .

Properties of water at $300\text{K}\text{, 1}\text{atm}$ .

  $v=0.858\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ , $\mathrm{Pr}=5.83$ .

Properties of engine oil at $300\text{K}\text{, 1}\text{atm}$ .

  $v=550\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ , $\mathrm{Pr}=6400$ .

Properties of mercury at $300\text{K}\text{, 1}\text{atm}$ .

  $v=0.113\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ , $\mathrm{Pr}=0.0248$ .

Concept used:

The equation of Reynolds number is $\mathrm{Re}=\frac{u_{\infty }{L}_1}{v}$ .

The formula for nusselt number is $Nu=\frac{\text{hL}}{\text{k}}$ .

The formula for average nusselt number is $\overline{Nu}=0.664{\mathrm{Re}}_x{}^{\frac{1}{2}}{\mathrm{Pr}}^{\frac{1}{3}}$ .

The formula of laminar $\delta$ and ${\delta }_t$ is $\delta =\frac{5x}{{\mathrm{Re}}_x{}^{\frac{1}{2}}}$ , ${\delta }_t=\frac{\delta }{{\mathrm{Pr}}^{\frac{1}{3}}}$ .

Nusselt number:

It is the ratio of convective heat transfer to convective heat transfer across a boundary.

  $\begin{array}{c}N{u}_L=\frac{\text{Convective}\text{heat}\text{transfer}}{\text{Conductive}\text{heat}\text{transfer}}\\ =\frac{h}{k\text{/}L}\\ =\frac{hL}{k}\end{array}$

Where $h$ is the convective heat transfer coefficient of the flow, $L$ is the characteristic length, $k$ is the thermal conductivity of the fluid.

Calculation:

Know that the equation of Reynolds number.

  $\mathrm{Re}=\frac{u_{\infty }{L}_1}{v}$

From the figure:

  

Put $0.04\text{m}$ from leading edge, $1\text{m/s}$ for velocity in Reynolds equation.

  $\begin{array}{c}\mathrm{Re}=\frac{1\text{m/s}\left(0.04\right)}{v}\\ =\frac{0.04{\text{m}}^{\text{2}}\text{/s}}{v}\end{array}$

Put $15.89\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ for velocity and obtain Reynolds number for air.

  $\begin{array}{c}{\mathrm{Re}}_{\text{air}}=\frac{0.04}{15.89\times {10}^{-6}}\\ =2517.30\end{array}$

Know that the formula of laminar $\delta$ and ${\delta }_t$ .

  $\delta =\frac{5x}{{\mathrm{Re}}_x{}^{\frac{1}{2}}}$ , ${\delta }_t=\frac{\delta }{{\mathrm{Pr}}^{\frac{1}{3}}}$

Put $0.04$ for length, $2517.30$ for Reynolds number and obtain laminar $\delta$ .

  $\begin{array}{c}\delta =\frac{5\times 0.04}{{\left(2517\right)}^{\frac{1}{2}}}\\ =0.003986\text{m}\end{array}$

Convert the unit of laminar $\delta$ from meter into millimeter.

  $\delta =3.99\text{mm}$

Know that the formula of laminar ${\delta }_t$ .

  ${\delta }_t=\frac{\delta }{{\mathrm{Pr}}^{\frac{1}{3}}}$

Put $3.99\text{mm}$ for laminar $\delta$ , $0.707$ for Prandtl number in equation of laminar ${\delta }_t$ .

  $\begin{array}{c}{\delta }_t=\frac{3.99}{{\left(0.707\right)}^{\frac{1}{3}}}\\ =4.48\text{mm}\end{array}$

Put $0.858\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ for velocity and obtain Reynolds number for water.

  $\begin{array}{c}{\mathrm{Re}}_{\text{water}}=\frac{0.04}{0.858\times {10}^{-6}}\\ =4.66\times {10}^4\end{array}$

Know that the formula of laminar $\delta$ .

  $\delta =\frac{5x}{{\mathrm{Re}}_x{}^{\frac{1}{2}}}$

Put $0.04$ for length, $4.66\times {10}^4$ for Reynolds number and obtain laminar $\delta$ .

  $\begin{array}{c}\delta =\frac{5\times 0.04}{{\left(4.66\times {10}^4\right)}^{\frac{1}{2}}}\\ =0.93\text{mm}\end{array}$

Know that the formula of laminar ${\delta }_t$ .

  ${\delta }_t=\frac{\delta }{{\mathrm{Pr}}^{\frac{1}{3}}}$

Put $0.93\text{mm}$ for laminar $\delta$ , $5.83$ for Prandtl number in equation of laminar ${\delta }_t$ .

  $\begin{array}{c}{\delta }_t=\frac{0.93}{{\left(5.83\right)}^{\frac{1}{3}}}\\ =0.52\text{mm}\end{array}$

Put $550\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ for velocity and obtain Reynolds number for engine oil.

  $\begin{array}{c}{\mathrm{Re}}_{\text{engine}\text{oil}}=\frac{0.04}{550\times {10}^{-6}}\\ =72.7\end{array}$

Know that the formula of laminar $\delta$ .

  $\delta =\frac{5x}{{\mathrm{Re}}_x{}^{\frac{1}{2}}}$

Put $0.04$ for length, $72.7$ for Reynolds number and obtain laminar $\delta$ .

  $\begin{array}{c}\delta =\frac{5\times 0.04}{{\left(72.7\right)}^{\frac{1}{2}}}\\ =23.5\text{mm}\end{array}$

Know that the formula of laminar ${\delta }_t$ .

  ${\delta }_t=\frac{\delta }{{\mathrm{Pr}}^{\frac{1}{3}}}$

Put $23.5\text{mm}$ for laminar $\delta$ , $6400$ for Prandtl number in equation of laminar ${\delta }_t$ .

  $\begin{array}{c}{\delta }_t=\frac{23.5}{{\left(6400\right)}^{\frac{1}{3}}}\\ =1.27\text{mm}\end{array}$

Put $0.013\times {10}^{-6}{\text{m}}^{\text{2}}\text{/s}$ for velocity and obtain Reynolds number for mercury.

  $\begin{array}{c}{\mathrm{Re}}_{\text{mercury}}=\frac{0.04}{0.113\times {10}^{-6}}\\ =3.54\times {10}^5\end{array}$

Know that the formula of laminar $\delta$ .

  $\delta =\frac{5x}{{\mathrm{Re}}_x{}^{\frac{1}{2}}}$

Put $0.04$ for length, $3.54\times {10}^5$ for Reynolds number and obtain laminar $\delta$ .

  $\begin{array}{c}\delta =\frac{5\times 0.04}{{\left(3.54\times {10}^5\right)}^{\frac{1}{2}}}\\ =0.34\text{mm}\end{array}$

Know that the formula of laminar ${\delta }_t$ .

  ${\delta }_t=\frac{\delta }{{\mathrm{Pr}}^{\frac{1}{3}}}$

Put $0.34\text{mm}$ for laminar $\delta$ , $0.0248$ for Prandtl number in equation of laminar ${\delta }_t$ .

  $\begin{array}{c}{\delta }_t=\frac{23.5}{{\left(0.0248\right)}^{\frac{1}{3}}}\\ =1.17\text{mm}\end{array}$

Conclusion:

Hence, the thermal boundary layer thickness for air, water, oil and mercury is 4.48, 0.52, 1.27, and 1.17 respectively.

To determine

To draw: the boundary layer thickness from the leading edge to a plate length of $40\text{mm}$ .

Answer to Problem 7.1P

Created the graph for determined values of thermal boundary layer thickness for air, water, oil and mercury is 4.48, 0.52, 1.27, and 1.17 respectively with the values oflaminar thermal boundary layer ${\partial }_{air}=3.99\text{mm}$ , ${\partial }_{water}=0.93\text{mm}$ , ${\partial }_{mercury}=0.34\text{mm}$ .

Explanation of Solution

Given Information:

The thermal boundary layer thickness for air, water, oil and mercury is 4.48, 0.52, 1.27, and 1.17 respectively.

Entire length $=40\text{mm}$ .

Boundary layer ${\partial }_{air}=3.99\text{mm}$

  ${\partial }_{water}=0.93\text{mm}$

  ${\partial }_{mercury}=0.34\text{mm}$

Concept used:

Plot the graph by Matlab software, obtained values by formulas correlation between Reynolds equation, Nusselt number, average nusselt number and boundary layer thickness.

Calculation:

Know that the determined values of thermal boundary layer thickness for air, water, oil, mercury are 4.48, 0.52, 1.27, and 1.17 respectively and determined values of the laminar thermal boundary layer are ${\partial }_{air}=3.99\text{mm}$ , ${\partial }_{water}=0.93\text{mm}$ , ${\partial }_{mercury}=0.34\text{mm}$ .

Substitute the values of thermal boundary layer thickness and laminar thermal boundary on the graph.

  

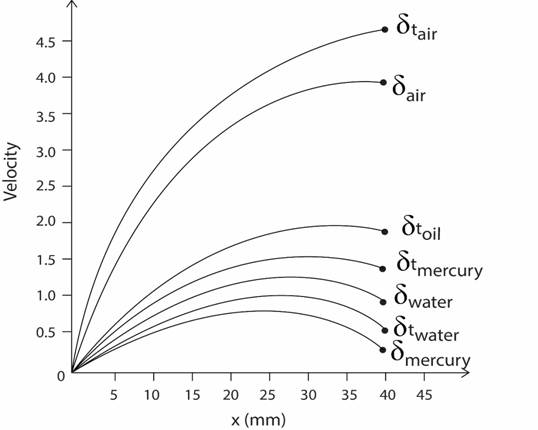
Conclusion:

Created the graph for determined values of thermal boundary layer thickness for air, water, oil and mercury is 4.48, 0.52, 1.27, and 1.17 respectively with the values oflaminar thermal boundary layer ${\partial }_{air}=3.99\text{mm}$ , ${\partial }_{water}=0.93\text{mm}$ , ${\partial }_{mercury}=0.34\text{mm}$ .