Chapter 67, Problem 31A

The length L of the point drill with included angle A can be calculated using the formula $L=k\varphi$where $\varphi$ is the diameter of the drill and $k=\frac{1}{2}\mathrm{tan\; <mo>\; (\; </mo>}°90°-\frac{A}{2}).$Determine k for each of the following angles. Round your answer to three decimal places.

To determine

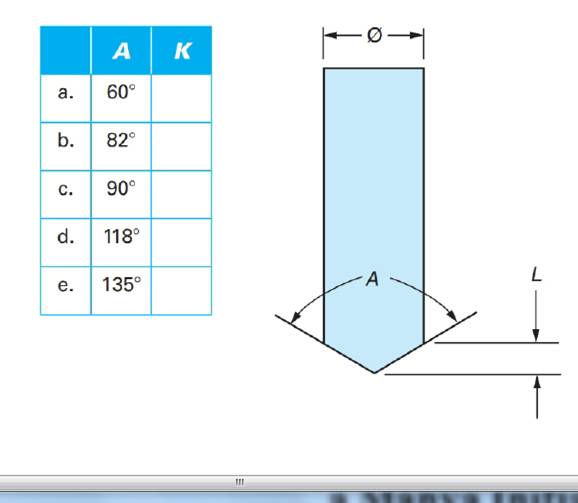
(a)

Find k for the given angle.

Answer to Problem 31A

  $k=0.866$

Explanation of Solution

Given information:

The relation:

$k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{A}{2}\right)$

The angle $A={60}^{\circ }$

Calculations:

Substituting the value $A={60}^{\circ }$ in the relation given for k:

  $\begin{array}{l}k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{{60}^{\circ }}{2}\right)\\ k=\frac{1}{2}\tan \left({60}^{\circ }\right)=\frac{1.732}{2}\\ \Rightarrow k=0.866\end{array}$

Conclusion:

The value of k is 0.866.

To determine

(b)

Find k for the given angle.

Answer to Problem 31A

  $k=0.575$

Explanation of Solution

Given information:

The relation:

$k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{A}{2}\right)$

The angle $A={82}^{\circ }$

Calculations:

Substituting the value $A={82}^{\circ }$ in the relation given for k:

  $\begin{array}{l}k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{{82}^{\circ }}{2}\right)\\ k=\frac{1}{2}\tan \left({49}^{\circ }\right)=\frac{1.150}{2}\\ \Rightarrow k=0.575\end{array}$

Conclusion:

The value of k is 0.575.

To determine

(c)

Find k for the given angle.

Answer to Problem 31A

  $k=0.5$

Explanation of Solution

Given information:

The relation:

$k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{A}{2}\right)$

The angle $A={90}^{\circ }$

Calculations:

Substituting the value $A={90}^{\circ }$ in the relation given for k:

  $\begin{array}{l}k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{{90}^{\circ }}{2}\right)\\ k=\frac{1}{2}\tan \left({45}^{\circ }\right)=\frac{1.000}{2}\\ \Rightarrow k=0.500\end{array}$

Conclusion:

The value of k is 0.500.

To determine

(d)

Find k for the given angle.

Answer to Problem 31A

  $k=0.300$

Explanation of Solution

Given information:

The relation:

$k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{A}{2}\right)$

The angle $A={118}^{\circ }$

Calculations:

Substituting the value $A={118}^{\circ }$ in the relation given for k:

  $\begin{array}{l}k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{{118}^{\circ }}{2}\right)\\ k=\frac{1}{2}\tan \left({31}^{\circ }\right)=\frac{0.600}{2}\\ \Rightarrow k=0.300\end{array}$

Conclusion:

The value of k is 0.300.

To determine

(e)

Find k for the given angle.

Answer to Problem 31A

  $k=0.207$

Explanation of Solution

Given information:

The relation:

$k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{A}{2}\right)$

The angle $A={135}^{\circ }$

Calculations:

Substituting the value $A={135}^{\circ }$ in the relation given for k:

  $\begin{array}{l}k=\frac{1}{2}\tan \left({90}^{\circ }-\frac{{135}^{\circ }}{2}\right)\\ k=\frac{1}{2}\tan \left({22.5}^{\circ }\right)=\frac{0.414}{2}\\ \Rightarrow k=0.207\end{array}$

Conclusion:

The value of k is 0.207.