
Finite Mathematics & Its Applications (12th Edition)
12th Edition
ISBN: 9780134437767
Author: Larry J. Goldstein, David I. Schneider, Martha J. Siegel, Steven Hair
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 6.3, Problem 33E
Street Routs Figure 1 shows a partial map of the streets in New York City. (Such maps are discussed in Chapter 5.) A tourist starts at point A and selects at random a shortest path to point B. That is, they walk only south and east. Find the probability that
(a) they pass through point C.
(b) they pass through point D.
(c) they pass through point C and point D.
(d) they pass through point C or point D.
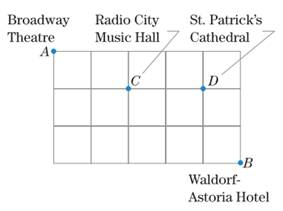
Figure 1
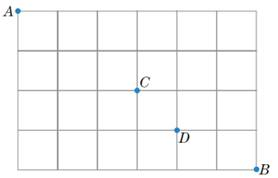
Figure 2
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Refer to page 15 for a problem involving evaluating a double integral in polar coordinates.
Instructions: Convert the given Cartesian integral to polar coordinates. Show all transformations
and step-by-step calculations.
Link
[https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]
Refer to page 9 for a problem requiring finding the tangent plane to a given surface at a point.
Instructions: Use partial derivatives to calculate the equation of the tangent plane. Show all
calculations
step-by-step.
Link [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]
Refer to page 8 for a problem involving solving a second-order linear homogeneous
differential equation.
Instructions: Solve using characteristic equations. Show all intermediate steps leading to the
general solution.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]
Chapter 6 Solutions
Finite Mathematics & Its Applications (12th Edition)
Ch. 6.1 - 1. Lightbulbs A machine produces lightbulbs. As...Ch. 6.1 - 2. Citrus Fruit Suppose that there are two crates...Ch. 6.1 - 1. Committee Selection A committee of two people...Ch. 6.1 - 2. Selecting Letters A letter is selected at...Ch. 6.1 - Heads and Tails An experiment consists of tossing...Ch. 6.1 - Four-Sided Dice A pair of four-sided dice-each...Ch. 6.1 - 5. Selecting from Urns Suppose that we have two...Ch. 6.1 - Coin Tosses An experiment consists of tossing a...Ch. 6.1 - 7. Efficiency Studies An efficiency expert records...Ch. 6.1 - Census Data A census taker records the annual...
Ch. 6.1 - Student Poll A campus survey is taken to correlate...Ch. 6.1 - 10. Automobiles An experiment consists of...Ch. 6.1 - 11. Let be a sample space,
.
a. Are E and F...Ch. 6.1 - 12. Draw the events E and E′ on two separate Venn...Ch. 6.1 - 13. Let be a sample space. Determine all possible...Ch. 6.1 - 14. Let S be a sample space with n outcomes. How...Ch. 6.1 - Let S={1,2,3,4} be a sample space, E={1}, and...Ch. 6.1 - 16. Let S be any sample space, and E, F any events...Ch. 6.1 - Coin Tosses Suppose that 10 coins are tossed and...Ch. 6.1 - Three-Digit Numbers An experiment consists of...Ch. 6.1 - Genetic Traits An experiment consists of observing...Ch. 6.1 - 20. Genetic Traits Consider the experiment and...Ch. 6.1 - 21. Shuttle Bus Suppose that you observe the...Ch. 6.1 - 22. Dice A pair of dice is rolled, and the sum of...Ch. 6.1 - Selecting Balls from an Urn An urn contains balls...Ch. 6.1 - Selecting Balls from an Urn Repeat Exercise 23 in...Ch. 6.1 - 25. NBA Draft Lottery In the NBA, the 14...Ch. 6.1 - Coin Die Suppose that a coin is tossed and a die...Ch. 6.1 - 27. The Game of Clue Clue is a board game in which...Ch. 6.2 - Solutions can be found following the section...Ch. 6.2 - Solutions can be found following the section...Ch. 6.2 - Prob. 3CYUCh. 6.2 - In Exercises 1–4, classify the type of probability...Ch. 6.2 - Prob. 2ECh. 6.2 - Prob. 3ECh. 6.2 - In Exercises 1–4, classify the type of probability...Ch. 6.2 - In Exercises 5 and 6, determine the probability...Ch. 6.2 - In Exercises 5 and 6, determine the probability...Ch. 6.2 - 7. Roulette The modern American roulette wheel has...Ch. 6.2 - U.S. States A state is selected at random from the...Ch. 6.2 - 9. Word Frequencies There are 4487 words in the...Ch. 6.2 - 10. United Nations Of the 193 member countries of...Ch. 6.2 - 11. Selecting a Letter An experiment consists of...Ch. 6.2 - 12. Selecting a Number An experiment consists of...Ch. 6.2 - Dice Suppose that a red die and a green die are...Ch. 6.2 - Children An experiment consists of observing the...Ch. 6.2 - Kind of High School The given table shows the...Ch. 6.2 - Highest Degree Planned The next table shows the...Ch. 6.2 - Grade Distributions The following table shows the...Ch. 6.2 - 18. Candy Colors The colors in a bag of...Ch. 6.2 - Prob. 19ECh. 6.2 - 20. An experiment with outcomes has the following...Ch. 6.2 - College Applications The table that follows was...Ch. 6.2 - 22. Employees’ Ages The next table summarizes the...Ch. 6.2 - 23. Which of the following probabilities are...Ch. 6.2 - 24. Which of the following probabilities are...Ch. 6.2 - Car Race Three cars, a Mazda, a Honda, and a Ford,...Ch. 6.2 - 26. Hair Color In a study, the residents of...Ch. 6.2 - 27. Political Views On a certain campus, the...Ch. 6.2 - 28. Tennis The probability that Alice beats Ben in...Ch. 6.2 - 29. Pair of Dice Suppose that a pair of dice is...Ch. 6.2 - Coin Tossing An experiment consists of tossing a...Ch. 6.2 - 31. Suppose that where E and F are mutually...Ch. 6.2 - Suppose that Pr(E)=.3andPr(EF)=.7, where E and F...Ch. 6.2 - In Exercises 33–36, consider the probabilities...Ch. 6.2 - In Exercises 3336, consider the probabilities...Ch. 6.2 - In Exercises 3336, consider the probabilities...Ch. 6.2 - In Exercises 3336, consider the probabilities...Ch. 6.2 - In Exercises 37–40, use a Venn diagram similar to...Ch. 6.2 - In Exercises 3740, use a Venn diagram similar to...Ch. 6.2 - In Exercises 3740, use a Venn diagram similar to...Ch. 6.2 - In Exercises 3740, use a Venn diagram similar to...Ch. 6.2 - 41. Convert the odds of “10 to 1” to a...Ch. 6.2 - Convert the odds of 4 to 5 to a probability.Ch. 6.2 - Convert the probability .2 to odds.Ch. 6.2 - Convert the probability 37 to odds.Ch. 6.2 - Coin Tosses The probability of getting three heads...Ch. 6.2 - Advanced Degree The probability that a graduate of...Ch. 6.2 - 47. Demographic The odds of a person in the...Ch. 6.2 - 48. Election Odds In March 2016, a betting website...Ch. 6.2 - Bookies Gamblers usually give odds against an...Ch. 6.2 - 50. Odds of an Earthquake The probability that...Ch. 6.2 - Prob. 51ECh. 6.2 - Prob. 52ECh. 6.3 - Solutions can be found following the section...Ch. 6.3 - Prob. 2CYUCh. 6.3 - 1. A number is chosen at random from the whole...Ch. 6.3 - 2. A number is chosen at random from the whole...Ch. 6.3 - 3. Balls in an Urn An urn contains five red balls...Ch. 6.3 - 4. Balls in an Urn An urn contains seven green...Ch. 6.3 - Balls in an Urn An urn contains six green balls...Ch. 6.3 - 6. Balls in an Urn An urn contains eight red balls...Ch. 6.3 - 7. Opinion Polling Two out of the seven members of...Ch. 6.3 - Opinion Polling Of the 15 members on a Senate...Ch. 6.3 - 9. Committee Selection In the 114th United States...Ch. 6.3 - 10. Committee Selection The U.S. Senate consists...Ch. 6.3 - 11. Quality Control A factory produces LCD panels,...Ch. 6.3 - Rotten Tomato A bag contains nine tomatoes, of...Ch. 6.3 - Selecting Students Exercises 13–16 refer to a...Ch. 6.3 - Selecting Students Exercises 1316 refer to a...Ch. 6.3 - Selecting Students Exercises 13–16 refer to a...Ch. 6.3 - Selecting Students Exercises 13–16 refer to a...Ch. 6.3 - 17. Birthday Three people are chosen at random....Ch. 6.3 - Birthday Four people are chosen at random. What is...Ch. 6.3 - 19. Date Conflict Without consultation with each...Ch. 6.3 - 20. Presidential Choices There were 16 presidents...Ch. 6.3 - Name Badges Eight workers need an employee number...Ch. 6.3 - Random Selection Each person in a group of 10...Ch. 6.3 - Birthday Problem What is the probability that, in...Ch. 6.3 - Birthday Problem Johnny Carson, host of The...Ch. 6.3 - Dice A die is rolled twice. What is the...Ch. 6.3 - Dice A die is rolled three times. What is the...Ch. 6.3 - Dice A die is rolled four times. What is the...Ch. 6.3 - Dice A die is rolled three times. What is the...Ch. 6.3 - 29. Coin Tosses A coin is tossed 10 times. What is...Ch. 6.3 - Coin Tosses A coin is tossed seven times. What is...Ch. 6.3 - Prob. 31ECh. 6.3 - 32. Elevator An elevator has six buttons: L, 1, 2,...Ch. 6.3 - Street Routs Figure 1 shows a partial map of the...Ch. 6.3 - Street Routes Repeat Exercise 33 for Fig. 2.Ch. 6.3 - 35. Baseball Predictions In the American League,...Ch. 6.3 - Baseball Predictions Suppose that the sportswriter...Ch. 6.3 - 37. Baseball Predictions Suppose that the...Ch. 6.3 - Baseball Predictions Suppose that the sportswriter...Ch. 6.3 - Place Settings Fred has five place settings...Ch. 6.3 - 40. Track Positions Michael and Christopher are...Ch. 6.3 - 41. Group Picture A man, a woman, and their three...Ch. 6.3 - 42. Letter Positions What is the probability that...Ch. 6.3 - Poker A poker hand consists of five cards drawn...Ch. 6.3 - Poker A poker hand consists of five cards drawn...Ch. 6.3 - Poker A poker hand consists of five cards drawn...Ch. 6.3 - Prob. 46ECh. 6.3 - Prob. 47ECh. 6.3 - Powerball Lottery The winner of the Powerball...Ch. 6.3 - Illinois Lotto Exercises 49 and 50 refer to the...Ch. 6.3 - Illinois Lotto Exercises 49 and 50 refer to the...Ch. 6.3 - 51. California Lottery In the California Fantasy 5...Ch. 6.3 - Prob. 52ECh. 6.3 - Prob. 53ECh. 6.3 - Prob. 54ECh. 6.3 - 55. Health Statistics Table 2 shows the...Ch. 6.3 - Prob. 56ECh. 6.3 - Prob. 57ECh. 6.3 - Prob. 58ECh. 6.3 - License Plate Game Johnny and Doyle are driving on...Ch. 6.3 - Prob. 60ECh. 6.3 - Prob. 61ECh. 6.3 - 62. Term Papers A political science class has 20...Ch. 6.3 - Prob. 63ECh. 6.3 - Prob. 64ECh. 6.3 - Prob. 65ECh. 6.3 - Prob. 66ECh. 6.4 - 1. Cards Suppose that there are three cards: one...Ch. 6.4 - Show that if events E and F are independent of...Ch. 6.4 - 1. The Venn diagram in Fig. 3 shows the...Ch. 6.4 - 2. The Venn diagram in Fig. 4 shows the...Ch. 6.4 - Let S be a sample space and E and F be events...Ch. 6.4 - Let S be a sample space and E and F be events...Ch. 6.4 - Let S be a sample space and E and F be events...Ch. 6.4 - 6. Let S be a sample space and E and F be events...Ch. 6.4 - Let S be a sample space and E and F be events...Ch. 6.4 - Let S be a sample space and E and F be events...Ch. 6.4 - Dice When a pair of dice is rolled, what is the...Ch. 6.4 - 10. Dice When a pair of dice is rolled, what is...Ch. 6.4 - Coins A coin is tossed three times. What is the...Ch. 6.4 - Coins A coin is tossed three times. What is the...Ch. 6.4 - Bag of Marbles A bag contains five red marbles and...Ch. 6.4 - Balls in an Urn Two balls are selected at random...Ch. 6.4 - 15. Children Suppose a family has two children and...Ch. 6.4 - Children Suppose a family has two children and at...Ch. 6.4 - 17. Value of College Twenty-five percent of...Ch. 6.4 - Advanced Degrees Sixty percent of the teachers at...Ch. 6.4 - Advanced Degrees Table 1 shows the projected...Ch. 6.4 - 20. Voting Table 2 shows the number of registered...Ch. 6.4 - Military Personnel Table 3 shows the numbers (in...Ch. 6.4 - 22. College Majors Table 4 shows the probable...Ch. 6.4 - 23. Bills in Envelopes Each of three sealed opaque...Ch. 6.4 - 24. Gold and Silver Coins Consider three boxes....Ch. 6.4 - 25. Cards A sequence of two playing cards is drawn...Ch. 6.4 - Cards A sequence of two playing cards is drawn at...Ch. 6.4 - Coin Tosses A coin is tossed five times. What is...Ch. 6.4 - Coin Tosses A coin is tossed twice. What is the...Ch. 6.4 - 29. Exit Polling According to exit polling for the...Ch. 6.4 - Population Twenty percent of the worlds population...Ch. 6.4 - 31. Basketball Suppose that your team is behind by...Ch. 6.4 - 32. Password Fred remembers all but the last...Ch. 6.4 - Let E and F be events with P(E)=.4,Pr(F)=.5, and...Ch. 6.4 - 34. Let E and F be events with , and. Are E and F...Ch. 6.4 - 35. Let E and F be independent events with . Find...Ch. 6.4 - 36. Let E and F be independent events with and ....Ch. 6.4 - In Exercises 3740, assume that E and F are...Ch. 6.4 - In Exercises 3740, assume that E and F are...Ch. 6.4 - In Exercises 37–40, assume that E and F are...Ch. 6.4 - In Exercises 3740, assume that E and F are...Ch. 6.4 - Let A, B, and C be independent events with...Ch. 6.4 - 42. Let A, B, and C be independent events with , ...Ch. 6.4 - 43. Balls in an Urn A sample of two balls is drawn...Ch. 6.4 - Balls in an Urn An urn contains two white balls...Ch. 6.4 - 45. Roll a Die Roll a die, and consider the...Ch. 6.4 - Roll a Die Roll a die, and consider the following...Ch. 6.4 - Rolling Dice Roll a pair of dice, and consider the...Ch. 6.4 - Rolling Dice Roll a pair of dice, and consider the...Ch. 6.4 - 49. Epidemiology A doctor studies the known cancer...Ch. 6.4 - 50. Blood Tests A hospital uses two tests to...Ch. 6.4 - Medical Screening A medical screening program...Ch. 6.4 - Guessing on an Exam A truefalse exam has 10...Ch. 6.4 - 53. System Reliability A TV set contains five...Ch. 6.4 - System Reliability In November 2015, Intel...Ch. 6.4 - 55. Smartphones Suppose that in Sleepy Valley, 70%...Ch. 6.4 - 56. Fishing The probability that a fisherman...Ch. 6.4 - Baseball A baseball players batting average...Ch. 6.4 - Roulette If you bet on the number 7 in roulette,...Ch. 6.4 - Free-Throws A basketball player makes each...Ch. 6.4 - 60. Free-Throws Rework Exercise 59 with a...Ch. 6.4 - Free-Throws Consider Exercise 59, but let the...Ch. 6.4 - Free-Throws Consider Exercise 59, but let the...Ch. 6.4 - Prob. 63ECh. 6.4 - 64. Coin Toss A coin is tossed five times. Is the...Ch. 6.4 - Prob. 65ECh. 6.4 - Prob. 66ECh. 6.4 - Prob. 67ECh. 6.4 - 68. Use the inclusion–exclusion principle for...Ch. 6.5 - Solutions can be found following the section...Ch. 6.5 - Solutions can be found following the section...Ch. 6.5 - Solutions can be found following the section...Ch. 6.5 - Solutions can be found following the section...Ch. 6.5 - In Exercises 1–4, draw trees representing the...Ch. 6.5 - In Exercises 1–4, draw trees representing the...Ch. 6.5 - Prob. 3ECh. 6.5 - In Exercises 1–4, draw trees representing the...Ch. 6.5 - Personnel Categories Refer to Exercise 3. What is...Ch. 6.5 - 6. Tax Returns Refer to Exercise 4. What is the...Ch. 6.5 - Personnel Categories Refer to Exercise 3. What is...Ch. 6.5 - Personnel Categories Refer to Exercise 3. What is...Ch. 6.5 - 9. Selecting from Urns Suppose that there is a...Ch. 6.5 - Cards, Coins, Dice A card is drawn from a 52-card...Ch. 6.5 - 11. Cards A card is drawn from a 52-card deck. We...Ch. 6.5 - 12. Balls in an Urn An urn contains six white...Ch. 6.5 - Quality Control Twenty percent of the library...Ch. 6.5 - Water Testing In a recent environmental study of...Ch. 6.5 - 15. Color Blindness Color blindness is a...Ch. 6.5 - Manufacturing A factory has two machines that...Ch. 6.5 - 17. T-maze A mouse is put into a T-maze (a maze...Ch. 6.5 - 18. T-maze Refer to Exercise 17. What is the...Ch. 6.5 - 19. Heads or Tails Three ordinary quarters and a...Ch. 6.5 - Prob. 20ECh. 6.5 - Tennis Kim has a strong first serve; whenever it...Ch. 6.5 - Tennis When a tennis player hits his first serve...Ch. 6.5 - 23. Accidental Nuclear War Suppose that, during...Ch. 6.5 - 24. Accidental Nuclear War Refer to Exercise 23....Ch. 6.5 - Coin Tosses A coin is to be tossed at most five...Ch. 6.5 - Cards Suppose that, instead of tossing a coin, the...Ch. 6.5 - Genetics Traits passed from generation to...Ch. 6.5 - 28. Genetics Refer to Exercise 27. Suppose that a...Ch. 6.5 - College Faculty At a local college, five sections...Ch. 6.5 - Quality Control A lightbulb manufacturer knows...Ch. 6.5 - 31. Balls in an Urn Urn I contains 5 red balls and...Ch. 6.5 - 32. Balls in an Urn An urn contains five red balls...Ch. 6.5 - Prob. 33ECh. 6.5 - 34. Selecting from Urns An urn contains four red...Ch. 6.5 - Industrial Production A factory that produces...Ch. 6.5 - Golf Bud is a very consistent golfer. On par-three...Ch. 6.5 - Nontransitive Dice Consider three dice: one red,...Ch. 6.5 - U.S. Car Production Car production in North...Ch. 6.5 - Prob. 39ECh. 6.5 - Prob. 40ECh. 6.5 - Prob. 41ECh. 6.5 - Prob. 42ECh. 6.5 - Prob. 43ECh. 6.5 - Prob. 44ECh. 6.5 - Medical Screening Suppose that a test for...Ch. 6.5 - Medical Screening The probability .0002 (or .02%)...Ch. 6.5 - 47. Medical Screening The results of a trial used...Ch. 6.5 - 48. Medical Screening The results of a trial used...Ch. 6.5 - Drug Testing Suppose that 500 athletes are tested...Ch. 6.5 - Polygraph Test Recent studies have indicated that...Ch. 6.6 - 1. Quality Control Refer to Example 2. Suppose...Ch. 6.6 - 2. Political Polling Use the method of natural...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 1–22, use Bayes’ theorem to calculate...Ch. 6.6 - In Exercises 1–22, use Bayes’ theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 1–22, use Bayes’ theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 1–22, use Bayes’ theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - Exercises 11–15 refer to diagnostic tests. A false...Ch. 6.6 - Exercises 11–15 refer to diagnostic tests. A false...Ch. 6.6 - Exercises 11–15 refer to diagnostic tests. A false...Ch. 6.6 - Exercises 11–15 refer to diagnostic tests. A false...Ch. 6.6 - Exercises 11–15 refer to diagnostic tests. A false...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 1–22, use Bayes’ theorem to calculate...Ch. 6.6 - Prob. 19ECh. 6.6 - In Exercises 1–22, use Bayes’ theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 122, use Bayes theorem to calculate...Ch. 6.6 - In Exercises 2330, use the method of natural...Ch. 6.6 - In Exercises 23–30, use the method of natural...Ch. 6.6 - Prob. 25ECh. 6.6 - Prob. 26ECh. 6.6 - In Exercises 23–30, use the method of natural...Ch. 6.6 - In Exercises 2330, use the method of natural...Ch. 6.6 - Prob. 29ECh. 6.6 - In Exercises 2330, use the method of natural...Ch. 6.7 - 1. Rolling a Die Simulate 36 rolls of a fair die....Ch. 6.7 - Prob. 2ECh. 6.7 - Free-Throws Simulate 10 free-throws for Kobe...Ch. 6.7 - Prob. 4ECh. 6.7 - Prob. 5ECh. 6.7 - Prob. 6ECh. 6.7 - Prob. 7ECh. 6.7 - Prob. 8ECh. 6.7 - 9. Gas Queue A gas station with four self-serve...Ch. 6.7 - Prob. 10ECh. 6 - 1. What is the sample space of an experiment?
Ch. 6 - 2. Using the language of sets and assuming that A...Ch. 6 - In a sample space, what is the probability of the...Ch. 6 - 4. What subset in a sample space corresponds to...Ch. 6 - Prob. 5FCCECh. 6 - Prob. 6FCCECh. 6 - Prob. 7FCCECh. 6 - Prob. 8FCCECh. 6 - Prob. 9FCCECh. 6 - Prob. 10FCCECh. 6 - Prob. 11FCCECh. 6 - Prob. 12FCCECh. 6 - Prob. 13FCCECh. 6 - Coins A box contains a penny, a nickel, a dime, a...Ch. 6 - Prob. 2RECh. 6 - 3. Suppose that E and F are events with . Find .
Ch. 6 - Suppose that E and F are mutually exclusive events...Ch. 6 - 5. Languages Of the 120 students in a class, 30...Ch. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - 9. Demographics Twenty-six percent of all...Ch. 6 - Prob. 10RECh. 6 - Prob. 11RECh. 6 - Prob. 12RECh. 6 - 13. Barrel of Apples Five of the apples in a...Ch. 6 - 14. Opinion Sampling Of the nine city council...Ch. 6 - Exam Questions Prior to taking an essay...Ch. 6 - 16. Craps In the casino game of craps, a player...Ch. 6 - Coin Tosses A coin is to be tossed five times....Ch. 6 - Coin Tosses Two players each toss a coin three...Ch. 6 - Olympic Swimmers In an Olympic swimming event, two...Ch. 6 - Prob. 20RECh. 6 - Prob. 21RECh. 6 - Drawing Cards A card is drawn at random from a...Ch. 6 - 23. Dice What is the probability of having each of...Ch. 6 - 24. Dice Find the odds in favor of getting four...Ch. 6 - Birthdays What is the probability that, out of a...Ch. 6 - Birthdays Four people are chosen at random. What...Ch. 6 - Let E and F be events with Pr(E)=.4,Pr(F)=.3, and...Ch. 6 - 28. Let E and F be events with . Find .
Ch. 6 - Coin Tosses When a coin is tossed three times,...Ch. 6 - 30. Dice Suppose that a pair of dice is rolled....Ch. 6 - Prob. 31RECh. 6 - Prob. 32RECh. 6 - 33. Premed Majors Suppose that a certain college...Ch. 6 - Prob. 34RECh. 6 - Prob. 35RECh. 6 - Coin Tosses Suppose that we toss a coin three...Ch. 6 - Prob. 37RECh. 6 - Prob. 38RECh. 6 - 39. Archery Two archers shoot at a moving target....Ch. 6 - 40. Final Exam Fred will do well on his final exam...Ch. 6 - Let A and B be independent events for which the...Ch. 6 - Let A and B be independent events with Pr(A)=.3...Ch. 6 - Prob. 43RECh. 6 - Prob. 44RECh. 6 - Prob. 45RECh. 6 - Prob. 46RECh. 6 - Left-Handedness According to a geneticist at...Ch. 6 - Tax Audits An auditing procedure for income tax...Ch. 6 - 49. Weighing Produce A supermarket has three...Ch. 6 - 50. Dragons An island contains an equal number of...Ch. 6 - Prob. 51RECh. 6 - Prob. 52RECh. 6 - Prob. 53RECh. 6 - Prob. 54RECh. 6 - Prob. 55RECh. 6 - Prob. 56RECh. 6 - First Paradox: Under certain circumstances, you...Ch. 6 - First Paradox: Under certain circumstances, you...Ch. 6 - First Paradox: Under certain circumstances, you...Ch. 6 - Prob. 4PCh. 6 - First Paradox: Under certain circumstances, you...Ch. 6 - Second Paradox: The probability of a male...Ch. 6 - Prob. 7PCh. 6 - Prob. 8PCh. 6 - Prob. 9PCh. 6 - Prob. 10PCh. 6 - Prob. 11P
Additional Math Textbook Solutions
Find more solutions based on key concepts
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
In Exercises 5-36, express all probabilities as fractions.
23. Combination Lock The typical combination lock us...
Elementary Statistics
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
With reference to Exercise 11.1 on page 398,
evaluate s2;
test the hypothesis that β1 = 0 against the alternati...
Probability and Statistics for Engineers and Scientists
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Refer to page 17 for a problem requiring solving a nonlinear algebraic equation using the bisection method. Instructions: Show iterative calculations for each step, ensuring convergence criteria are satisfied. Clearly outline all steps. Link [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forwardProblem: The probability density function of a random variable is given by the exponential distribution Find the probability that f(x) = {0.55e−0.55x 0 < x, O elsewhere} a. the time to observe a particle is more than 200 microseconds. b. the time to observe a particle is less than 10 microseconds.arrow_forwardThe OU process studied in the previous problem is a common model for interest rates. Another common model is the CIR model, which solves the SDE: dX₁ = (a = X₁) dt + σ √X+dWt, - under the condition Xoxo. We cannot solve this SDE explicitly. = (a) Use the Brownian trajectory simulated in part (a) of Problem 1, and the Euler scheme to simulate a trajectory of the CIR process. On a graph, represent both the trajectory of the OU process and the trajectory of the CIR process for the same Brownian path. (b) Repeat the simulation of the CIR process above M times (M large), for a large value of T, and use the result to estimate the long-term expectation and variance of the CIR process. How do they compare to the ones of the OU process? Numerical application: T = 10, N = 500, a = 0.04, x0 = 0.05, σ = 0.01, M = 1000. 1 (c) If you use larger values than above for the parameters, such as the ones in Problem 1, you may encounter errors when implementing the Euler scheme for CIR. Explain why.arrow_forward
- Refer to page 1 for a problem involving proving the distributive property of matrix multiplication. Instructions: Provide a detailed proof using matrix definitions and element-wise operations. Show all calculations clearly. Link [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 30 for a problem requiring solving a nonhomogeneous differential equation using the method of undetermined coefficients. Instructions: Solve step-by-step, including the complementary and particular solutions. Clearly justify each step. Link [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 5 for a problem requiring finding the critical points of a multivariable function. Instructions: Use partial derivatives and the second partial derivative test to classify the critical points. Provide detailed calculations. Link [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forward
- Refer to page 3 for a problem on evaluating limits involving indeterminate forms using L'Hôpital's rule. Instructions: Apply L'Hôpital's rule rigorously. Show all derivatives and justify the steps leading to the solution. Link [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forward3. Let {X} be an autoregressive process of order one, usually written as AR(1). (a) Write down an equation defining X₁ in terms of an autoregression coefficient a and a white noise process {} with variance σ². Explain what the phrase "{} is a white noise process with variance o?" means. (b) Derive expressions for the variance 70 and the autocorrelation function Pk, k 0,1,. of the {X} in terms of o2 and a. Use these expressions to suggest an estimate of a in terms of the sample autocor- relations {k}. (c) Suppose that only every second value of X is observed, resulting in a time series Y X2, t = 1, 2,.... Show that {Y} forms an AR(1) process. Find its autoregression coefficient, say d', and the variance of the underlying white noise process, in terms of a and o². (d) Given a time series data set X1, ..., X256 with sample mean = 9.23 and sample autocorrelations ₁ = -0.6, 2 = 0.36, 3 = -0.22, p = 0.13, 5 = -0.08, estimate the autoregression coefficients a and a' of {X} and {Y}.arrow_forward#8 (a) Find the equation of the tangent line to y = √x+3 at x=6 (b) Find the differential dy at y = √x +3 and evaluate it for x=6 and dx = 0.3arrow_forward
- Refer to page 96 for a problem involving the heat equation. Solve the PDE using the method of separation of variables. Derive the solution step-by-step, including the boundary conditions. Instructions: Stick to solving the heat equation. Show all intermediate steps, including separation of variables, solving for eigenvalues, and constructing the solution. Irrelevant explanations are not allowed. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardQ.2 Q.4 Determine ffx dA where R is upper half of the circle shown below. x²+y2=1 (1,0)arrow_forwardRefer to page 83 for a vector field problem requiring verification of conservative nature and finding a scalar potential function. Instructions: Focus strictly on verifying conditions for conservativeness and solving for the potential function. Show all work step-by-step. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL


College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY