
To calculate: The
Answer to Problem 16E
The value of the integral
Explanation of Solution
Given:
The integral is
Concept used:
If a nonnegative function
Formula used:
The area of the semicircle is as follows:
Here, the expression
Calculation:
In the given integral, the integrand function is
The equation of circle for the semicircle
Comparing this with the standard equation of circle
Now draw the graph of
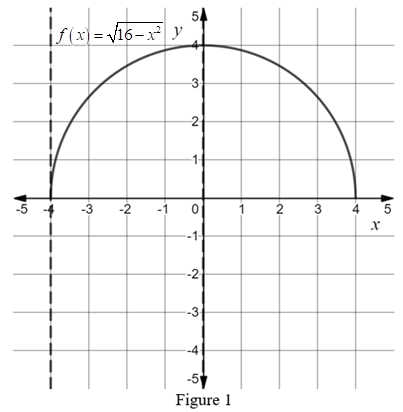
It can be seen that the area under a curve from
It can be seen from Figure 1 that the radius of the semicircle is 4. The area of the region is also half of the semicircle.
Use the formula of the semicircle to obtain the area of the semicircle.
The area of the region is half of the area of the semicircle, thus the area of the region under the curve is
Therefore, by the concept the value of the integral is equal to the area of the region.
The value of the integral
Conclusion:
Thus, the value of the integral
Chapter 6 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Calculus: Early Transcendentals (2nd Edition)
University Calculus: Early Transcendentals (4th Edition)
Algebra and Trigonometry (6th Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





