
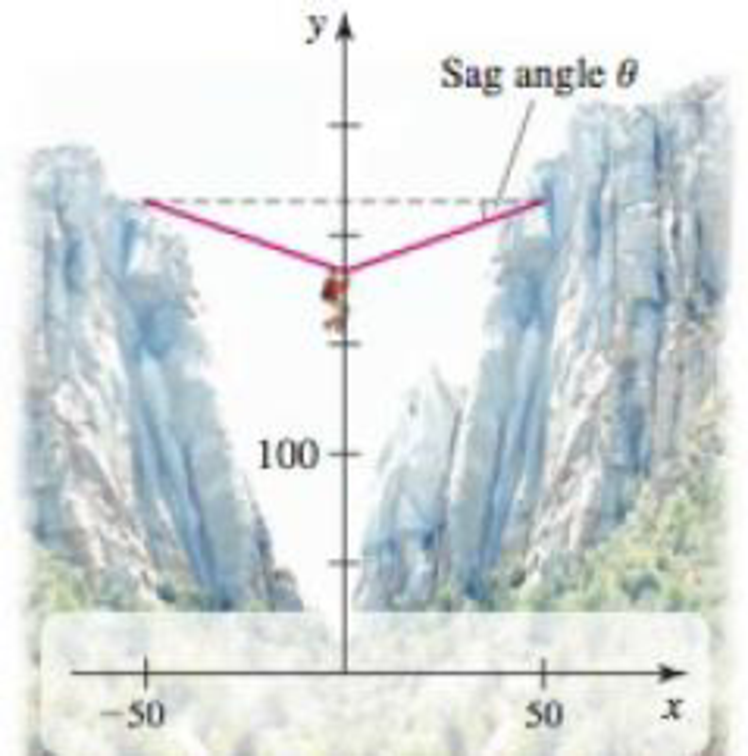
Sag angle Imagine a climber clipping onto the rope described in Example 7 and pulling himself to the rope’s midpoint. Because the rope is supporting the weight of the climber, it no longer takes the shape of the catenary y = 200 cosh(x/200). Instead, the rope (nearly) forms two sides of an isosceles triangle. Compute the sag angle θ illustrated in the figure, assuming that the rope does not stretch when weighted. Recall from Example 7 that the length of the rope is 101 ft.
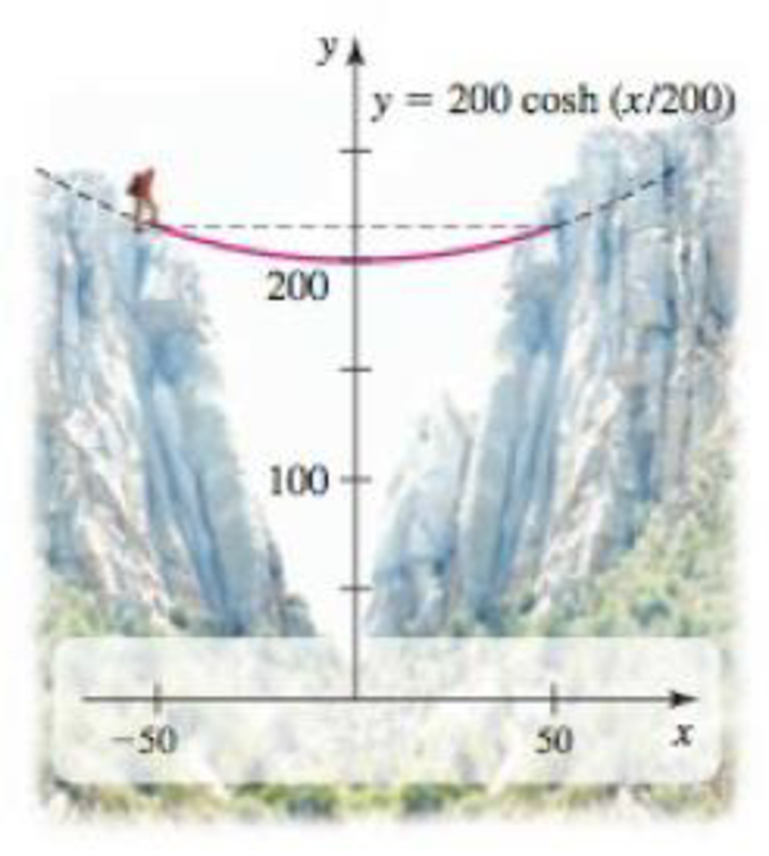
EXAMPLE 7 Length of a catenary A climber anchors a rope at two points of equal height, separated by a distance of 100 ft, in order to perform a Tyrolean traverse. The rope follows the catenary f(x) = 200 cosh(x/200) over the interval [−50, 50] (Figure 6.98). Find the length of the rope between the two anchor points.
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Calculus: Early Transcendentals (2nd Edition)
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Pre-Algebra Student Edition
Intro Stats, Books a la Carte Edition (5th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics: Picturing the World (7th Edition)
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning  Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL



