
Concept explainers
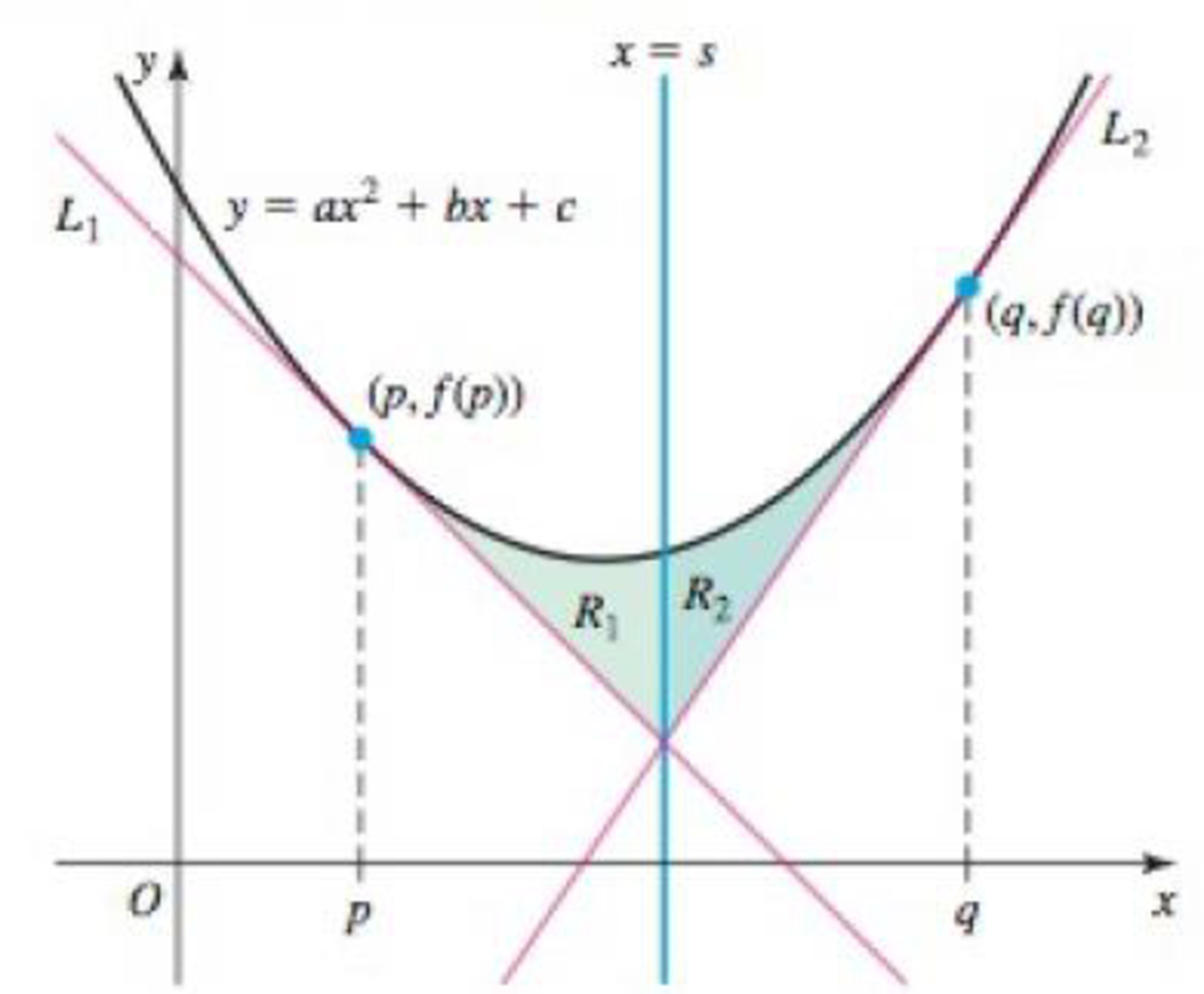
Equal area property for parabolas Let f(x) = ax2 + bx + c be an arbitrary quadratic function and choose two points x = p and x= q. Let L1 be the line tangent to the graph of f at the point (p, f(p)) and let L2 be the line tangent to the graph at the point (q, f(q)). Let x = s be the vertical line through the intersection point of L1 and L2. Finally, let R1, be the region bounded by y =f(x), L1, and the vertical line x = s, and let R2 be the region bounded by y = f(x), L2, and the vertical line x = s. Prove that the area of R1 equals the area of R2.
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Calculus: Early Transcendentals (2nd Edition)
Additional Math Textbook Solutions
Thinking Mathematically (6th Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics (13th Edition)
Elementary Statistics
Algebra and Trigonometry (6th Edition)
- = Q6 What will be the allowable bearing capacity of sand having p = 37° and ydry 19 kN/m³ for (i) 1.5 m strip foundation (ii) 1.5 m x 1.5 m square footing and (iii)1.5m x 2m rectangular footing. The footings are placed at a depth of 1.5 m below ground level. Assume F, = 2.5. Use Terzaghi's equations. 0 Ne Na Ny 35 57.8 41.4 42.4 40 95.7 81.3 100.4arrow_forwardQ1 The SPT records versus depth are given in table below. Find qan for the raft 12% foundation with BxB-10x10m and depth of raft D-2m, the allowable settlement is 50mm. Elevation, m 0.5 2 2 6.5 9.5 13 18 25 No.of blows, N 11 15 29 32 30 44 0 estigate shear 12%arrow_forwardQ2 A/ State the main field tests which may be carried out to investigate shear strength of a soil layer? B/ What are the main factors that affecting the spacing and number of boreholes for a given project? C/ Illustrate the causes of disturbance of Shelby tubes samples.arrow_forward
- Trolley of the overhead crane moves along the bridge rail. The trolley position is measured from the center of the bridge rail (x = 0) is given by x(t) = 0.5t^3-6t^2+19.5t-14 : 0 <= t <= 3 min. The trolley moves from point A to B in the forward direction, B to C in the reverse direction and C to D again in the forward direction. CONTROL PANEL END TRUCK- RUNWAY BEAM- BRIDGE RAIL HOIST -TROLLEY TROLLEY BUMPER TROLLEY DRIVE LPENDANT TRACK -TROLLEY CONDUCTOR TRACK WIRE ROPE -HOOK BLOCK -BRIDGE DRIVE -END TRUCK BUMPER -RUNWAY RAIL TROLLEY END STOP -CONDUCTOR BAR PENDANT FESTOONING TROLLEY FESTOONING PENDANT CABLE PENDANT x(t)=0.5t^3-6t^2+19.5t-14 v(t)=1.5t^2-12t+19.5 a(t)=(dv(t))/dt=3t-12 Fig. T2.2: The overhead crane Total masses of the trolley, hook block, and the load attached to the hook block are 110 kg, 20 kg, and 150 kg. Damping coefficient, D, is 40 kg/s. What is the total amount of energy required from the trolley motor to move the system [Hint: Use Newton's 2nd law to obtain the…arrow_forwardCONTROL PANEL- BRIDGE RAIL HOIST -TROLLEY TROLLEY BUMPER -BRIDGE DRIVE END TRUCK- RUNWAY BEAM- END TRUCK BUMPER -RUNWAY RAIL TROLLEY DRIVE TROLLEY END STOP -CONDUCTOR BAR LPENDANT TRACK TROLLEY CONDUCTOR TRACK -WIRE ROPE PENDANT FESTOONING TROLLEY FESTOONING -PENDANT CABLE -HOOK BLOCK PENDANTarrow_forwardchool Which of the following functions describes the graph of g(x)--2√9-x²+37 9 8 7 6 4 2 -10-9-8-7-6-5-4-3-2-1 1 -1 -2 -4 -6 10 9 8 B 5 4 3 3 6 -10-9-8-7-6-5-4-3-2-1 2 3 4 6 1 -2 4 -5 -6 -8 -9 -10 10 -10-9-8-7-6-5-4-3-2-1 9 8 Lessons Assessments 6 5 4 + 2 1 1 2 3 4 5 6 8 -1 2 4 -5 -B 8 10 10 9 8 7 6 5 4 3 2 1 -10-9-8-7-6-5-4-3-2-1 1 2 3 4 5 6 B 9 10 -1 -2 -3 -5arrow_forward
- Please sketch questions 1, 2 and 6arrow_forwardsolve questions 3, 4,5, 7, 8, and 9arrow_forward4. Please solve this for me and show every single step. I am studying and got stuck on this practice question, and need help in solving it. Please be very specific and show every step. Thanks. I WANT A HUMAN TO SOLVE THIS PLEASE.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage


