Chapter 56, Problem 25AR

To determine

The angle $\angle 1$.

The angle $\angle 2$.

The angle $\angle 3$.

The angle $\angle 4$.

The angle $\angle 5$.

The angle $\angle 6$.

The angle $\angle 7$.

The angle $\angle 8$.

The angle $\angle 9$.

The angle $\angle 10$.

Answer to Problem 25AR

The angle $\angle 1$ is $32°$.

The angle $\angle 2$ is $58°$.

The angle $\angle 3$ is $17°$.

The angle $\angle 4$ is $15°$.

The angle $\angle 5$ is $32°$.

The angle $\angle 6$ is $20°$.

The angle $\angle 7$ is $38°$.

The angle $\angle 8$ is $21°$.

The angle $\angle 9$ is $69°$.

The angle $\angle 10$ is $122°$.

Explanation of Solution

Given information:

The angle $\stackrel{⌢}{AC}$ is $116°$, the angle $\stackrel{⌢}{EC}$ is $140°$, the angle $\stackrel{⌢}{EF}$ is $64°$ and the angle $\stackrel{⌢}{CH}$ is $42°$.

Draw the diagram for the pattern.

  

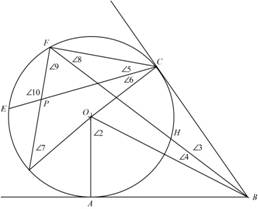
        Figure -(1)

Write the expression for the angle $\angle 5$.

 $\angle 5=\frac{1}{2}\stackrel{⌢}{EF}$ ...... (I)

Here, the angle of the curve $FE$ is $\stackrel{⌢}{EF}$.

Write the expression for the angle $\angle 8$.

 $\angle 8=\frac{1}{2}\stackrel{⌢}{CH}$ ...... (II)

Here, the angle of the curve $CH$ is $\stackrel{⌢}{CH}$.

Write the expression for the angle $\angle 9$.

 $\angle 9=90°-\angle 8$ ...... (III)

Write the expression for the angle $\angle CPF$.

 $\angle CPF=180°-\left(\angle 5+\left(\angle 8+\angle 9\right)\right)$ ...... (IV)

Write the expression for the angle $\angle 10$.

 $\angle 10=180°-\angle CPF$ ...... (V)

Write the expression for the $\angle DOA$.

 $\angle DOA=180°-\stackrel{⌢}{AC}$ ...... (VI)

Here, the angle of the curve $AC$ is $\stackrel{⌢}{AC}$.

Write the expression for the curve angle $\stackrel{⌢}{ED}$.

 $\stackrel{⌢}{DE}=360°-\left(\stackrel{⌢}{DA}+\stackrel{⌢}{AC}+\stackrel{⌢}{EC}\right)$ ...... (VII)

Here, the angle of the curve $DE$ is $\stackrel{⌢}{DE}$, the angle of the curve $DA$ is $\stackrel{⌢}{DA}$, the angle of the curve $CE$ is $\stackrel{⌢}{EC}$.

Write the expression for the angle $\angle 6$.

 $\angle 6=\frac{1}{2}\stackrel{⌢}{DE}$ ...... (VIII)

Write the expression for the angle $\angle 7$.

 $\angle 7=180°-\left(\angle 6+\angle CPD\right)$ ...... (IX)

Write the expression for the curve angle $\stackrel{⌢}{CF}$.

 $\stackrel{⌢}{CF}=360°-\left(\stackrel{⌢}{AC}+\stackrel{⌢}{EF}+\stackrel{⌢}{ED}+\stackrel{⌢}{DA}\right)$ ...... (X)

Write the expression for the angle $\angle 3$.

 $\angle 3=\frac{1}{2}\left(\stackrel{⌢}{CF}-\stackrel{⌢}{CH}\right)$ ...... (XI)

Write the expression for the angle $\angle 4$.

 $\angle 4=180°-\left(90°+58°+\angle 3\right)$ ...... (XII)

Write the expression for the angle between the tangent $\left(AB\right)$ and $\left(BC\right)$.

 $\angle ABC=\frac{1}{2}\left(\stackrel{⌢}{CDA}-\stackrel{⌢}{AC}\right)$ ...... (XIII)

Write the expression for the angle $\angle 1$.

 $\begin{array}{l}\angle ABC=\angle 1+\angle 4+\angle 3\\ \angle 1=\angle ABC-\left(\angle 4+\angle 3\right)\end{array}$ ...... (XIV)

Write the expression for the angle $\angle 2$.

 $\angle 2=180°-\left(\angle 1+90°\right)$ ...... (XV)

Calculation:

Substitute $64°$ for $\stackrel{⌢}{FE}$ in Equation (I).

 $\begin{array}{c}\angle 5=\frac{1}{2}\left(64°\right)\\ =32°\end{array}$

Substitute $42°$ for $\stackrel{⌢}{CH}$ in Equation (II).

 $\begin{array}{c}\angle 8=\frac{1}{2}\left(42°\right)\\ =21°\end{array}$

Substitute $21°$ for $\angle 8$ in Equation (III).

 $\begin{array}{c}\angle 9=90°-21°\\ =69°\end{array}$

Substitute $21°$ for $\angle 8$, $32°$ for $\angle 5$ and $69°$ for $\angle 9$ in Equation (IV).

 $\begin{array}{c}\angle CPF=180°-\left(32°+\left(21°+69°\right)\right)\\ =180°-122°\\ =58°\end{array}$

Substitute $58°$ for $\angle CPF$ in Equation (V).

 $\begin{array}{c}\angle 10=180°-58°\\ =122°\end{array}$

Substitute $116°$ for $\stackrel{⌢}{AC}$ in Equation (VI).

 $\begin{array}{c}\angle DOA=180°-116°\\ =64°\end{array}$

Substitute $64°$ for $\stackrel{⌢}{DA}$, $116°$ for $\stackrel{⌢}{AC}$ and $140°$ for $\stackrel{⌢}{EC}$ in Equation (VII).

 $\begin{array}{c}\stackrel{⌢}{DE}=360°-\left(64°+116°+140°\right)\\ =360°-\left(320°\right)\\ =40°\end{array}$

Substitute $40°$ for $\stackrel{⌢}{DE}$ in Equation (VIII).

 $\begin{array}{c}\angle 6=\frac{1}{2}\left(40°\right)\\ =20°\end{array}$

Substitute $122°$ for $\angle CPD$ and $20°$ for $\angle 6$ in Equation (IX).

 $\begin{array}{c}\angle 7=180°-\left(20°+122°\right)\\ =180°-\left(142°\right)\\ =38°\end{array}$

Substitute $64°$ for $\stackrel{⌢}{EF}$, $116°$ for $\stackrel{⌢}{AC}$, $64°$ for $\stackrel{⌢}{DA}$ and $40°$ for $\stackrel{⌢}{ED}$ in Equation (X).

 $\begin{array}{c}\stackrel{⌢}{CF}=360°-\left(116°+64°+40°+64°\right)\\ =360°-\left(284°\right)\\ =76°\end{array}$

Substitute $76°$ for $\stackrel{⌢}{CF}$ and $42°$ for $\stackrel{⌢}{CH}$ in Equation (XI).

 $\begin{array}{c}\angle 3=\frac{1}{2}\left(76°-42°\right)\\ =\frac{1}{2}\left(34°\right)\\ =17°\end{array}$

Substitute $17°$ for $\angle 3$ in Equation (XII).

 $\begin{array}{c}\angle 4=180°-\left(90°+58°+17°\right)\\ =180°-\left(165°\right)\\ =15°\end{array}$

Substitute $244°$ for $\stackrel{⌢}{CDA}$ and $116°$ for $\stackrel{⌢}{AC}$ in Equation (XIII).

 $\begin{array}{c}\angle ABC=\frac{1}{2}\left(244°-116°\right)\\ =\frac{1}{2}\left(128°\right)\\ =64°\end{array}$

Substitute $64°$ for $\angle ABC$, $15°$ for $\angle 4$ and $17°$ for $\angle 3$ in Equation (XIV).

 $\begin{array}{c}\angle 1=64°-\left(15°+17°\right)\\ =64°-32°\\ =32°\end{array}$

Substitute $32°$ for $\angle 1$ in Equation (XV).

 $\begin{array}{c}\angle 2=180°-\left(32°+90°\right)\\ =180°-\left(122°\right)\\ =58°\end{array}$

Conclusion:

The angle $\angle 1$ is $32°$.

The angle $\angle 2$ is $58°$.

The angle $\angle 3$ is $17°$.

The angle $\angle 4$ is $15°$.

The angle $\angle 5$ is $32°$.

The angle $\angle 6$ is $20°$.

The angle $\angle 7$ is $38°$.

The angle $\angle 8$ is $21°$.

The angle $\angle 9$ is $69°$.

The angle $\angle 10$ is $122°$.