Chapter 5.3, Problem 11P

Sports: Surfing In Hawaii, January is a favorite month for surfing since 60% of the days have a surf of at least 6 feet (Reference: Hawaii Data Book, Robert C. Schmitt). You work day shifts in a Honolulu hospital emergency room. At the beginning of each month you select your days off, and you pick 7 days at random in January to go surfing. Let r be the number of days the surf is at least 6 feet.

1. (a) Make a histogram of the probability distribution of r.
2. (b) What is the probability of getting 5 or more days when the surf is at least 6 feet?
3. (c) What is the probability of getting fewer than 3 days when the surf is at least 6 feet?
4. (d) What is the expected number of days when the surf will be at least 6 feet?
5. (e) What is the standard deviation of the r-probability distribution?
6. (f) Interpretation Can you be fairly confident that the surf will be at least 6 feet high on one of your days off? Explain.

To determine

Construct a histogram for the probabilities of given successes.

Answer to Problem 11P

The histogram of binomial distribution for the number of days with $n=7$ and $p=0.60$ is shown below:

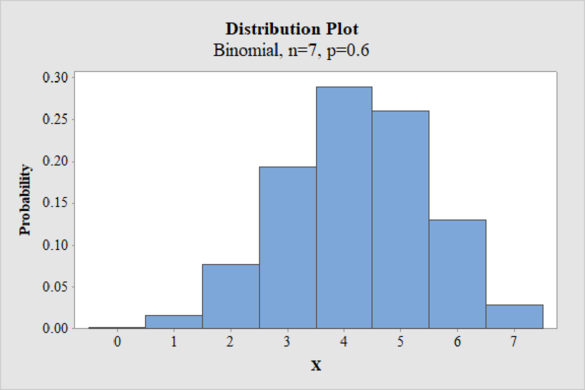
Explanation of Solution

Let r follow a binomial distribution that represents the number of days the surf’s height is at least 6 feet.

Total number of days picked in January (or trials) $n=7$.

Probability of days that have surf’s height of at least 6 feet (or success) $p=0.60$.

Use Table 3, Appendix II: Binomial distribution table, the probability values for $n=7$ and $p=0.60$ for $r=0,1,2,3,4,5,6and\text{ 7}$ is given as follows:

$r$	Probability
0	0.002
1	0.017
2	0.077
3	0.194
4	0.290
5	0.261
6	0.131
7	0.028

Step-by-step procedure to draw the histogram using MINITAB software:

• Choose Graph > Bar Chart.
• From Bars represent, choose Values from a table.
• Under One column of values, choose Simple. Click OK.
• In Graph variables, enter the column of Probability.
• In Categorical variable, enter the column of r.
• Click OK.

Thus, the histogram of binomial distribution for the number of days with $n=7$ and $p=0.60$ is obtained.

Interpretation:

From the histogram, it can be observed that the distribution is approximately symmetric as it has a bell-shaped curve.

To determine

Calculate the probability of getting at least 5 days if the surf's height is at least 6 feet.

Answer to Problem 11P

The probability of getting at least 5 days is 0.420.

Explanation of Solution

Calculation:

The probability of getting 5 or more days if the surf's height is at least 6 feet is calculated as given below:

$\begin{array}{l}P\left(r\ge 5\right)=P\left(5\right)+P\left(6\right)+P\left(7\right)\\ =0.261+0.131+0.028\\ (u\sin gbinomialdistributiontable)\\ =0.420\end{array}$

Use Table 3, Appendix II: Binomial distribution table, the probability values for $n=7$ and $p=0.60$ for $r=5,6,7$ are 0.261, 0.131, and 0.028.

Thus, the probability of getting 5 or more days if the surf's height is at least 6 feet is 0.420.

Interpretation:

There is 42% chance of getting 5 or more days if the surf's height is at least 6 feet.

To determine

Calculate the probability of getting less than 3 days if the surf's height is at least 6 feet.

Answer to Problem 11P

The probability of getting less than 3 days is 0.096.

Explanation of Solution

Calculation:

The probability of getting less than 3 days if the surf's height is at least 6 feet is calculated as given below:

$\begin{array}{l}P\left(r<3\right)=P\left(r\le 2\right)\\ =P\left(0\right)+P\left(1\right)+P\left(2\right)\\ \text{ = }0.002+0.017+0.077\\ (u\sin gbinomialdistributiontable)\\ =0.096\end{array}$

Use Table 3, Appendix II: Binomial distribution table, the probability values for $n=7$ and $p=0.60$ for $r=0,1,2$ are 0.002, 0.017, and 0.077.

Thus, the probability of getting less than 3 days if the surf's height is at least 6 feet is 0.096.

Interpretation:

There is 9.6% chance of getting less than 3 days if the surf's height is at least 6 feet.

To determine

Calculate the expected number of days if the surf's height is at least 6 feet.

Answer to Problem 11P

The expected number of days is 4.2.

Explanation of Solution

Calculation:

The expected value of a number of days if the surf's height is at least 6 feet is calculated as given below:

$\begin{array}{c}\mu =np\\ =7\times 0.60\\ =4.2\end{array}$

Thus, the expected value of number of days if the surf's height is at least 6 feet is 4.2.

Interpretation:

One can expect 4.2 days if the surf's height is at least 6 feet.

To determine

Calculate the standard deviation of r-distribution.

Answer to Problem 11P

The standard deviation is 1.296.

Explanation of Solution

Calculation:

The standard deviation of r-distribution is calculated as given below:

$\begin{array}{c}\sigma =\sqrt{npq}\\ =\sqrt{np\left(1-p\right)}\\ =\sqrt{7\times 0.60\times \left(1-0.60\right)}\\ =1.296\end{array}$

Thus, the standard deviation of probability distribution of r is 1.296.

To determine

Describe whether one can be confident that the surf’s height will be at least 6 feet on one of the days off.

Answer to Problem 11P

Yes, one can be fairly confident as the expected number of days the surf’s height will be at least 6 feet is 4.

The probability of getting at least one day is 0.998.

Explanation of Solution

Calculation:

The probability of getting at least 1 day if the surf's height is at least 6 feet is calculated as given below:

$\begin{array}{l}P\left(r\ge 1\right)=1-P\left(0\right)\\ =1-0.002\\ (\text{using }binomialdistributiontable)\\ =0.998\end{array}$

Use Table 3, Appendix II: Binomial distribution table, the probability value for $n=7$ and $p=0.60$ for $r=0$ is 0.002.

Thus, the probability of getting at least 1 day if the surf's height is at least 6 feet is 0.998.

Interpretation:

The expected number of days the surf’s height will be at least 6 feet is 4 and there is 99.8% chance of getting surf’s height that is at least 6 feet on at least one of the days off. Hence, one can be confident of obtaining it.