Chapter 5.2, Problem 63P

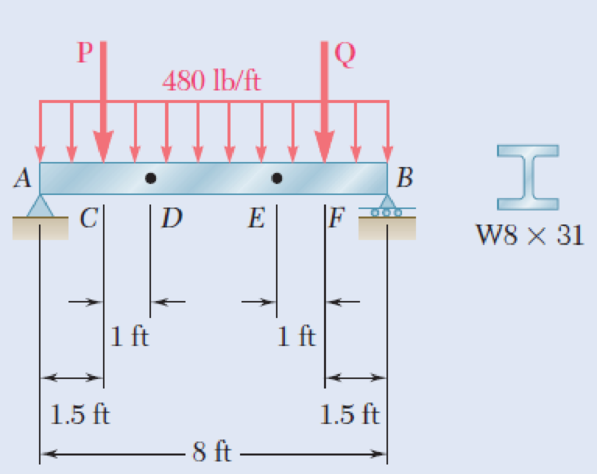
The beam AB supports a uniformly distributed load of 480 lb/ft and two concentrated loads P and Q. The normal stress due to bending on the bottom edge of the lower flange is +14.85 ksi at D and +10.65 ksi at E. (a) Draw the shear and bending-moment diagrams for the beam. (b) Determine the maximum normal stress due to bending that occurs in the beam.

Fig. P5.63

To determine

Draw the shear and bending-moment diagrams for the beam.

Explanation of Solution

Given information:

The normal stress due to bending at the point D is ${\sigma }_{D\left(\text{Lower}\right)}=+14.85\text{ksi}$.

The normal stress due to bending at the point E is ${\sigma }_{E\left(\text{Lower}\right)}=+10.65\text{MPa}$

Refer to Appendix C “Properties of Rolled-Steel Sections” in the textbook.

The section modulus (S) for $\text{W}8\times 31$ section is $S=27.5\text{in}{\text{.}}^3$.

Determine the bending moment at point D $\left(M_D\right)$ using the relation.

$M_D={\sigma }_{D}S$

Here, the normal stress at point D is ${\sigma }_D$.

Substitute 14.85 ksi for ${\sigma }_D$ and $27.5\text{in}{\text{.}}^3$ for S.

$\begin{array}{c}{M}_D=14.85\text{ksi}\times 27.5\\ =408.375\text{kip-in}\text{.}\times \frac{\text{1}\text{ft}}{\text{12}\text{in}\text{.}}\\ =34.03125\text{kip-ft}\end{array}$

Determine the bending moment at point E $\left(M_E\right)$ using the relation.

$M_E={\sigma }_{E}S$

Here, the normal stress at point E is ${\sigma }_E$.

Substitute 10.65 ksi for ${\sigma }_E$ and $27.5\text{in}{\text{.}}^3$ for S.

$\begin{array}{c}{M}_E=10.65\times 27.5\\ =292.875\text{kip-in}\text{.}\times \frac{\text{1}\text{ft}}{\text{12}\text{in}\text{.}}\\ =24.40625\text{kip-ft}\end{array}$

Show the free-body diagram of the region DE as in Figure 1.

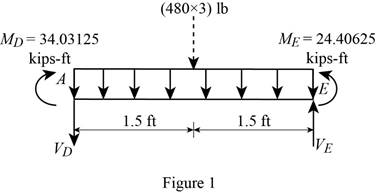
Determine the vertical reaction at point D by taking moment about point E.

$\begin{array}{l}{\displaystyle \sum M_E=0}\\ M_E-M_D+\left(480\text{lb}\times \frac{\text{1}\text{kip}}{\text{1000}\text{lb}}\times 3\right)\times 1.5+V_D\left(3\right)=0\\ 24.40625-34.03125+2.16+3V_D=0\\ V_D=2.488\text{kips}\end{array}$

Show the free body diagram of the region ACD as in Figure 2.

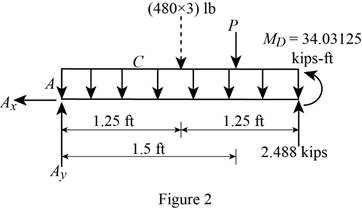
Determine the magnitude of the load P by taking moment about the point A.

$\begin{array}{l}{\displaystyle \sum M_A=0}\\ -P\left(1.5\right)-\left(480\text{lb}\times \frac{\text{1}\text{kip}}{\text{1000}\text{lb}}\times 2.5\right)\times 1.25+M_D+2.488\left(2.5\right)=0\\ -1.5P-1.5+34.03125+6.22=0\\ P=25.83\text{kips}\end{array}$

Determine the vertical reaction at point A by resolving the vertical component of forces.

$\begin{array}{l}{\displaystyle \sum F_y=0}\\ A_y-\left(480\text{lb}\times \frac{\text{1}\text{kip}}{\text{1000}\text{lb}}\times 2.5\right)+2.488-P=0\\ A_y-1.2+2.488-25.83=0\\ A_y=24.54\text{kips}\end{array}$

Show the free body diagram of the entire beam as in Figure 3.

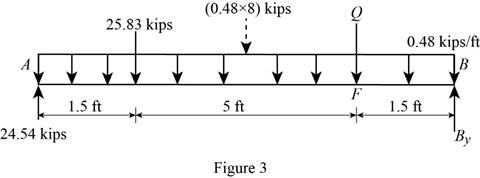
Determine the magnitude of the load P by taking moment about the point B.

$\begin{array}{l}{\displaystyle \sum M_B=0}\\ 24.54\left(8\right)-25.83\left(6.5\right)-\left(0.48\times 8\right)\times 4-Q\left(1.5\right)=0\\ 196.32-167.895-15.36-1.5Q=0\\ Q=8.71\text{kips}\end{array}$

Determine the vertical reaction at point A by resolving the vertical component of forces.

$\begin{array}{l}{\displaystyle \sum F_y=0}\\ 24.54-25.83-\left(0.48\times 8\right)-Q+B_y=0\\ -1.29-3.84-8.71+B_y=0\\ B_y=13.84\text{kips}\end{array}$

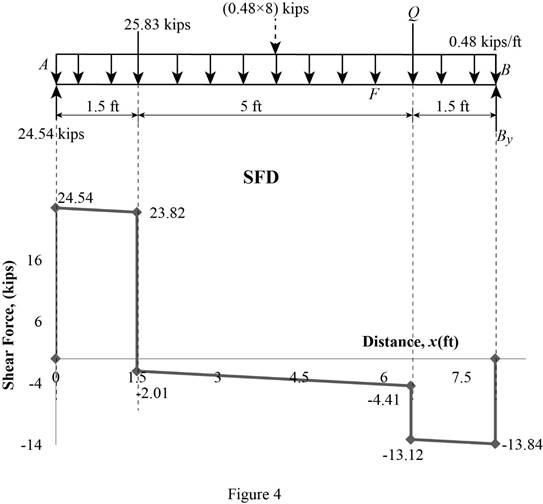
Shear force:

Show the calculation of shear force as follows;

$V_A=24.54\text{kips}$

$\begin{array}{c}{V}_C-V_A=-0.48\times 1.5\\ V_C^{Left}=-0.72+V_A\\ =-0.72+24.54\\ =23.82\text{kips}\end{array}$

$\begin{array}{c}{V}_C^{Right}=23.82-25.83\\ =-2.01\text{kips}\end{array}$

$\begin{array}{c}{V}_F-V_C=-25.83-0.48\times 5\\ V_F^{Left}=-25.83-2.4+V_C\\ =-28.23+23.82\\ =-4.41\text{kips}\end{array}$

$\begin{array}{c}{V}_F^{Right}=-4.41-8.71\\ =-13.12\text{kips}\end{array}$

$\begin{array}{c}{V}_B-V_E=-8.71-0.48\times 1.5\\ V_B=-8.71-0.72+V_E\\ =-9.43-4.41\\ =-13.84\text{kips}\end{array}$

Show the calculated shear force values as in Table 1.

Location (x) ft	Shear force (V) kips
A	24.54
C (Left)	23.82
C (Right)	–2.01
F (Left)	–4.41
F (Right)	–13.12
B	–13.84

Plot the shear force diagram as in Figure 4.

Bending moment:

Show the calculation of the bending moment as follows;

$M_A=0$

$\begin{array}{c}{M}_C-M_A=23.82\times 1.5+\frac{1}{2}\times \left(24.54-23.82\right)\times 1.5\\ M_C=35.73+0.54+M_A\\ =36.27+0\\ =36.27\text{kips-ft}\end{array}$

$\begin{array}{c}{M}_F-M_C=-2.01\times 5-\frac{1}{2}\times \left(4.41-2.01\right)\times 5\\ M_E=-10.05-6+M_C\\ =-16.5+36.27\\ =19.77\text{kips-ft}\end{array}$

$M_B=0$

Show the calculated bending moment values as in Table 2.

Location (x) ft	Bending moment (M) kips-ft
A	0
C	36.27
F	19.77
B	0

Plot the bending moment diagram as in Figure 5.

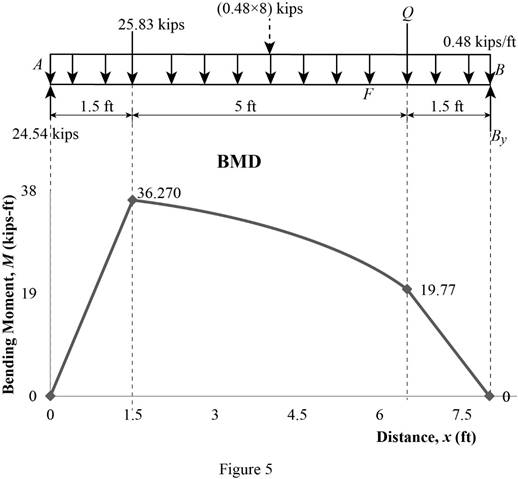
Refer to Figure 5;

The maximum absolute bending moment is $\left|M_{\max }\right|=36.27\text{kips-ft}$.

To determine

The maximum normal stress due to bending.

Answer to Problem 63P

The maximum normal stress due to bending is $\underset{\_}{15.82\text{ksi}}$.

Explanation of Solution

Given information:

Refer to Appendix C “Properties of Rolled-Steel Sections” in the textbook.

The section modulus (S) for $\text{W}8\times 31$ section is $S=27.5\text{in}{\text{.}}^3$.

The maximum absolute bending moment is $\left|M_{\max }\right|=36.27\text{kips-ft}$.

Determine the maximum normal stress $\left({\sigma }_m\right)$ using the equation.

${\sigma }_m=\frac{\left|M\right|}{S}$

Substitute $36.27\text{kips-ft}$ for M and $27.5\text{in}{\text{.}}^3$ for S.

$\begin{array}{c}{\sigma }_m=\frac{36.27\text{kips-ft}\times \frac{\text{12}\text{in}\text{.}}{\text{1}\text{ft}}}{27.5}\\ =15.82\text{ksi}\end{array}$

Therefore, the maximum normal stress due to bending is $\underset{\_}{15.82\text{ksi}}$.