
Concept explainers
A 1.00-kg glider on a horizontal air track is pulled by a string at an angle θ. The taut string runs over a pulley and is attached to a hanging object of mass 0.500 kg as shown in Figure P5.40. (a) Show that the speed vx of the glider and the speed vy of the hanging object are related by vx = uvy, where u = z(z2 − h02)−1/2. (b) The glider is released from rest. Show that at that instant the acceleration ax of the glider and the acceleration ay of the hanging object are related by ax = uay. (c) Find the tension in the string at the instant the glider is released for h0 = 80.0 cm and θ = 30.0°.
Figure P5.40
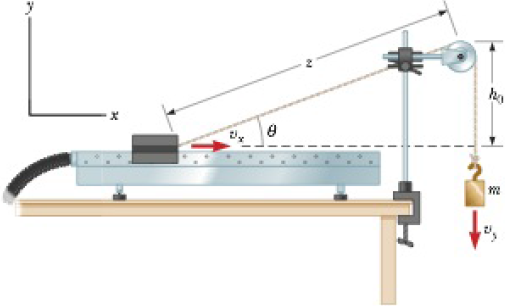
(a)
The relation between the speed of the glider and the speed of the hanging object.
Answer to Problem 5.76AP
The relation between the speed of the glider and the speed of the hanging object is
Explanation of Solution
The mass of the glider is
The free body diagram of the given case is as shown below.
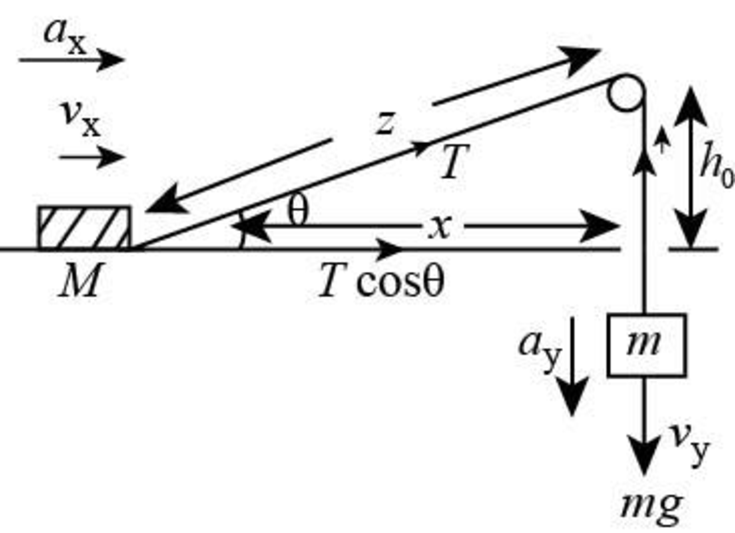
Figure (1)
Form the above figure (1).
Write the expression for the length of the string using Pythagorean Theorem,
Here,
Rearrange the above equation for
Write the expression for the speed of the glider
Here,
Substitute
The term
Write the expression for the speed of the hanging object.
Here,
Substitute
Substitute
Conclusion:
Therefore, the relation between the speed of the glider and the speed of the hanging object is
(b)
The relation between the acceleration of the glider and the speed of the hanging object.
Answer to Problem 5.76AP
The relation between the acceleration of the glider and the speed of the hanging object is
Explanation of Solution
From equation (2), the relation of
Write the expression for the acceleration of the glider
Substitute
The initial velocity of the hanging object is zero.
Substitute
Here,
Conclusion:
Therefore, the relation between the acceleration of the glider and the speed of the hanging object is
(c)
The tension of the string.
Answer to Problem 5.76AP
The tension of the string is
Explanation of Solution
From the free body diagram in figure (1) the net direction in
From part (a) the value of
Substitute
Substitute
Thus, the value of
The net force in
Here,
Substitute
Rearrange the above equation for
The net force in the
Here,
Form part (b) substitute
From equation (3) substitute
Conclusion:
Substitute
Therefore, the tension in the string is
Want to see more full solutions like this?
Chapter 5 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- Suppose a heart defibrillator passes 10.5 Amps of current through a patient's torso for 5.0 x 10-3 seconds in order to restore a regular heartbeat. The voltage across the defibrillator is 9800 volts for the entire time that current is flowing. If 7.25 kg of body tissue is involved, with a specific heat of 3500 J/(kg°C), then what is the resulting temperature increase of the person's torso? (Give your answer as the number of degrees C.)arrow_forwardThe figure below is a cross-sectional view of a coaxial cable. The center conductor is surrounded by a rubber layer, an outer conductor, and another rubber layer. In a particular application, the current in the inner conductor is I₁ = 1.04 A out of the page and the current in the outer conductor is I2 = 2.90 A into the page. Assuming the distance d = 1.00 mm, answer the following. 4 12 (a) Determine the magnitude and direction of the magnetic field at point a. magnitude 208 direction upward (b) Determine the magnitude and direction of the magnetic field at point b. magnitude direction 238 You can approach this problem by finding the field produced by current I₁ and the field produced by I2 and then adding them vectorially. μT downwardarrow_forwardShoto, from My Hero Academia, has a power (or a “quirk”) that allows him to make large amounts of ice from nothing. Let us say that due to a fire a 361 kg steel beam is heated to 943.˚C and Shoto creates 390. kg of ice at 0.00˚C around it to cool it down. What is the final temperature of the system after the ice melts and it reaches thermal equilibrium? The specific heat of steel is 502 J/kg˚C. The specific heat of water is 4186 J/kg˚C. The latent heat of fusion for ice is 3.33⋅10^5 J/kg.arrow_forward
- A 25.0 cm long organ pipe is filled with air and is open at one end and closed at the other. The speed of sound in air at 0°C is 331 m/s. What is the frequency of the fourth mode of vibration? Multiple Choice О 1,550 Hz О 1,750 Hz О 2,320 Hz О 2,720 Hz О 3,170 Hzarrow_forward23.4 g of coffee beans at room temperature (18.6 °C) is mixed into 316 g of water at 96.8 °C in an effort to make coffee. The entire system is poured in a 363 g ceramic mug. Assume the mug is initally also at room temperature (18.6 °C). What is the final temperature of the mixture? The specific heat of ground coffee beans is 1670 J/kg˚C, the specific heat of water is 4186 J/kg˚C, and the specific heat of the mug is 850. J/kg˚C.arrow_forwardSnoop Dogg, in an effort to get laid back (with his mind on his money and his money on his mind) pours himself a gin and juice. He mixes 0.124 kg (about 3 shots) of gin with 0.576 kg (about a pint) of orange juice. The gin starts at 20.0˚C, room temperature. The juice is refrigerated and starts at 2.89 ˚C. What is the final temperature after mixing of the gin and juice? The specific heat of gin is 3460 J/kg˚C and the specific heat of orange juice is 3730 J/kg˚C.arrow_forward
- A sword is heated up to 226 °C, it is put into a nearby barrel of water that is at 18.4 °C. What mass of water would be needed to cool the sword to 30.0˚C, bringing the system to thermal equilibrium? The sword is 35.4 kg and is made of steel. The specific heat of water is = 4186 J/kg ˚C. The specific heat of steel is = 502 J/kg ˚Carrow_forwardYou are planning on installing a new above-ground swimming pool in your backyard. The pool will be rectangular with dimensions 32.0 m x 10.0 m. It will be filled with fresh water to a depth of 2.20 m. In order to provide the appropriate structural support, you wish to determine the following. (a) Determine the force exerted on the bottom of the pool by the water (in N). (No Response) N (b) Determine the force exerted on each end of the pool by the water (in N). (Assume the end is the 10.0 m wall.) (No Response) N (c) Determine the force exerted on each side of the pool by the water (in N). (Assume the side is the 32.0 m wall.) (No Response) N (d) You wish to have swimming parties with your children and grandchildren. At a given time, you might have 23 people with an average mass of 75.0 kg in the pool. You need to determine if such parties will affect your calculations for the required strength of materials supporting your pool. The parties will not affect the required strength since…arrow_forwardThe construction of a water pistol is shown in the figure below. The cylinder with cross-sectional area A₁ is filled with water and when the piston is pushed (by pulling the trigger), water is forced out the tube with cross-sectional area A2. The radius of the cylinder and tube are, respectively, 1.30 cm and 1.10 mm, and the center of the tube is a height h = 3.00 cm above the center of the cylinder. (Assume atmospheric pressure is 1.013 × 105 Pa.) A2 A₁ (a) If the pistol is fired horizontally at a height of 1.30 m, determine the time interval (in s) required for water to travel from the nozzle to the ground. Neglect air resistance. (No Response) s (b) If the desired range of the stream is 7.50 m, with what speed ✓2 (in m/s) must the stream leave the nozzle? (No Response) m/s (c) At what speed v₁ (in m/s) must the plunger be moved to achieve the desired range? (No Response) m/s (d) What is the pressure (in Pa) at the nozzle? (No Response) Pa (e) Find the pressure (in Pa) needed in the…arrow_forward
- A high-speed lifting mechanism supports a(n) 700-kg object with a steel cable that is 34.0 m long and 4.00 cm² in cross-sectional area. (a) Determine the elongation of the cable. (Enter your answer to at least two decimal places.) (No Response) mm (b) By what additional amount does the cable increase in length if the object is accelerated upwards at a rate of 2.5 m/s²? (No Response) mm (c) What is the greatest mass that can be accelerated upward at 2.5 m/s² if the stress in the cable is not to exceed the elastic limit of the cable, which is 2.2 × 108 Pa? (No Response) kgarrow_forwardA square metal sheet 2.5 cm on a side and of negligible thickness is attached to a balance and inserted into a container of fluid. The contact angle is found to be zero, as shown in Figure a, and the balance to which the metal sheet is attached reads 0.42 N. A thin veneer of oil is then spread over the sheet, and the contact angle becomes 180°, as shown in Figure b. The balance now reads 0.41 N. What is the surface tension of the fluid? x Your response differs from the correct answer by more than 10%. Double check your calculations. N/m a barrow_forwardA helium-filled balloon (whose envelope has a mass of m₁ = 0.260 kg) is tied to a uniform string of length l = 2.70 m and mass m = 0.050 6 kg. The balloon is spherical with a radius of r = 0.399 m. When released in air of temperature 20°C and density Pair = 1.20 kg/m³, it lifts a length h of string and then remains stationary as shown in the figure below. We wish to find the length of string lifted by the balloon. He (a) When the balloon remains stationary, what is the appropriate analysis model to describe it? Oa particle in equilibrium model a particle under constant acceleration model a particle under constant velocity model the ideal fluid model (b) Write a force equation for the balloon from this model in terms of the buoyant force B, the weight F of the balloon, the weight Fe of the helium, and the weight F of the segment of string of length h. (Use any variable or symbol stated above along with the following as necessary: π. Follow the sign convention that upward is the positive…arrow_forward
 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





