
Concept explainers
a.
To find the intervals on which the function is increasing by using analytical method.
a.
Answer to Problem 14RE
The function
Explanation of Solution
Given:
The function is
Calculation:
The function
Now put
Below is graph
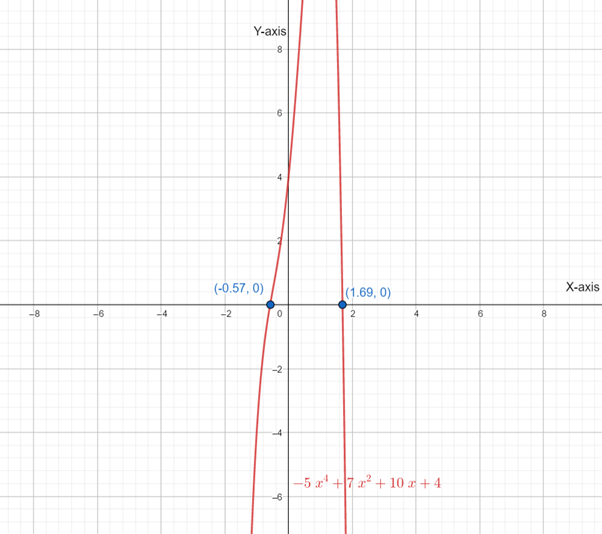
Therefore ,the critical points are
So , there are three intervals that is
put
put
put
Therefore , the function is increasing in interval
Below is the graph of
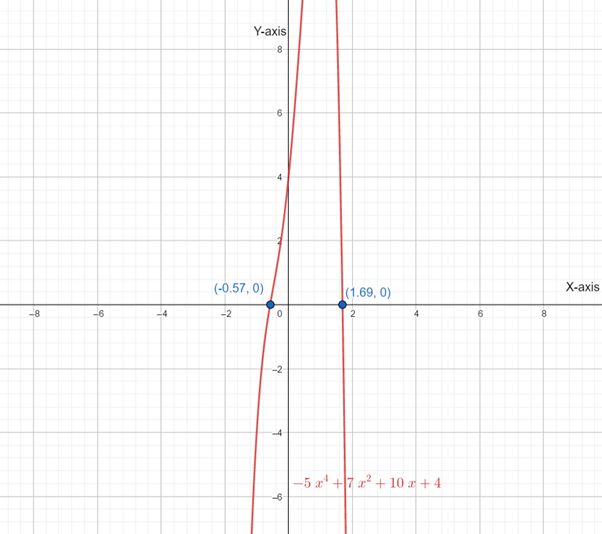
From graph of
b.
To find the intervals on which the function is decreasing by using analytical method.
b.
Answer to Problem 14RE
The function is decreasing in interval is
Explanation of Solution
Given:
The function is
Calculation:
The function
Now put
Below is graph
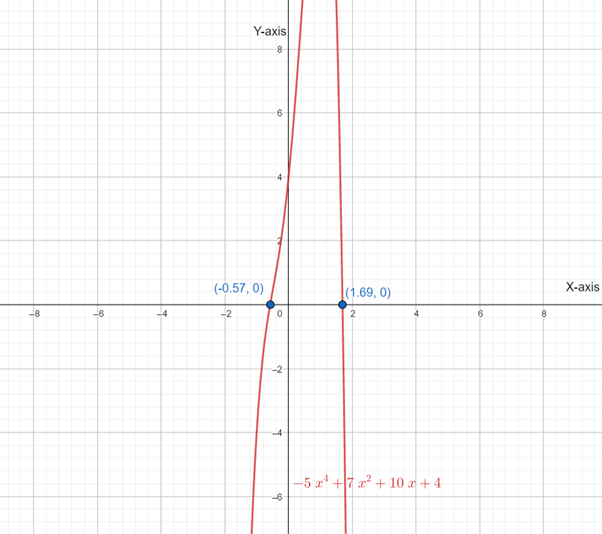
Therefore ,the critical points are
So , there are three intervals that is
put
put
put
Therefore , the function is decreasing in interval is
Below is the graph of
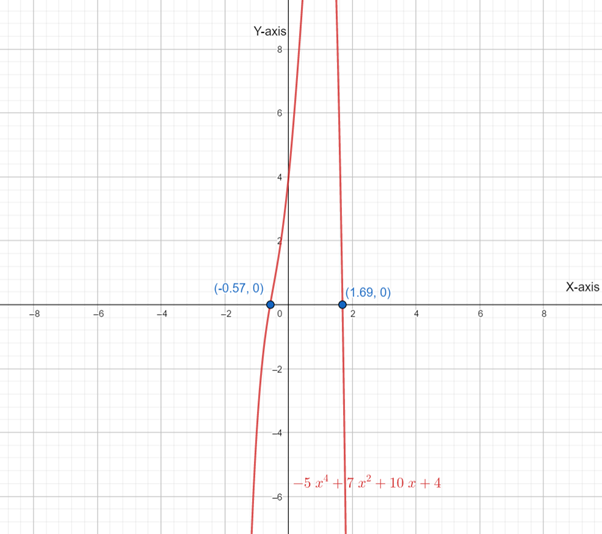
From graph of
c.
To find the intervals on which the function is concave up by using analytical method.
c.
Answer to Problem 14RE
The Function
Explanation of Solution
Given:
The function is
Calculation:
The graph of a twice differentiable function
Concave up on any interval where
Since,
First derivative :
Second derivative :
Now, put
Therefore , there are two intervals that is
check the value of
Now for
Now for
Therefore, the Function
Below is the graph of
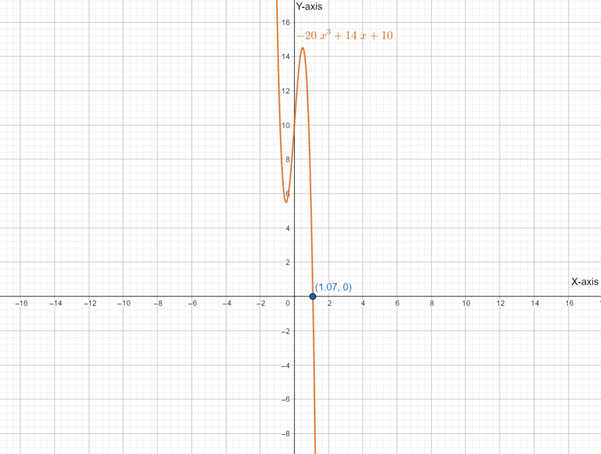
From graph it is clear that, the Function
d.
To find the intervals on which the function is concave down by using analytical method.
d.
Answer to Problem 14RE
The Function
Explanation of Solution
Given:
The function is
Calculation:
The graph of a twice differentiable function
Concave up on any interval where
Since,
First derivative :
Second derivative :
Now, put
Therefore , there are two intervals that is
check the value of
Now for
Now for
Therefore, the Function
Below is the graph of
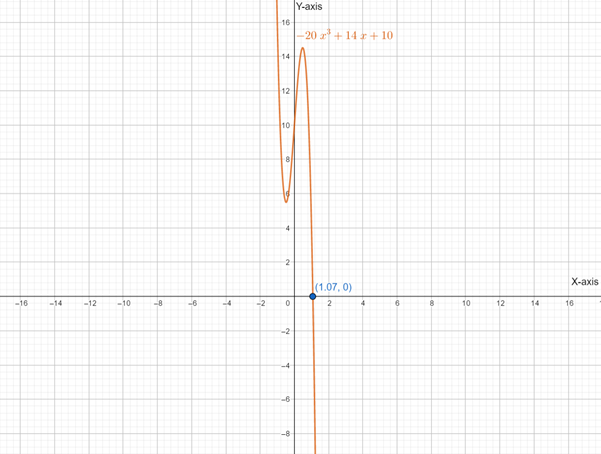
From graph it is clear that, the Function
e.
To find any local extreme values.
e.
Answer to Problem 14RE
The function
Explanation of Solution
Given:
The function is
Calculation:
Graph of
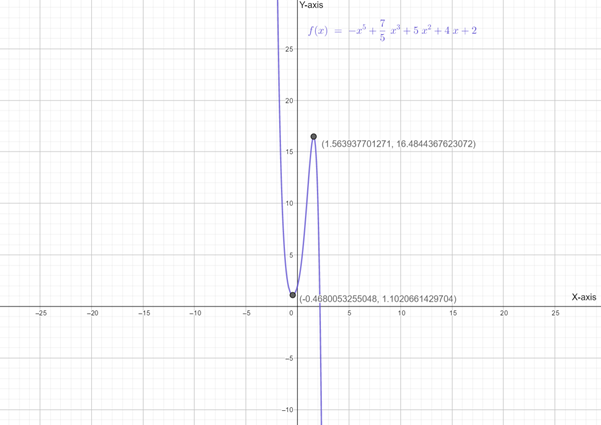
From graph it is clear that the function
f.
To find inflections points.
f.
Answer to Problem 14RE
The inflection point is at
Explanation of Solution
Given:
The function is
Calculation:
Inflection point of any function is a point where the graph of function has a tangent line and where the concavity changes.
Since,
Therefore, the inflection point is at
Chapter 5 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Elementary Statistics (13th Edition)
University Calculus: Early Transcendentals (4th Edition)
College Algebra with Modeling & Visualization (5th Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





