Chapter 4.7, Problem 15PPS

(a)

To determine

To Graph:

Draw a graph to represent the cost of using a taxi cab.

Explanation of Solution

Given Information:

Lauren wants to take a taxi from a hotel to a friend’s house.The rate is $3 plus $1.50 per mile after the first mile . Every fraction of a mile is rounded up to the next mile.

Concept Used:

Least Integer Function:

The function whose value at any number x is the smallest integer greater than of equal to x is called the least integer function.

It is denoted by $\lceil x\rceil$ . It is also known as ceiling of x .

For example

  $\begin{array}{l}\lceil 3.578\rceil =4\\ \lceil 0.78\rceil =1\\ \lceil -4.64\rceil =-4\end{array}$

Calculation:

The rate of taxi cab = $3

Extra charges per mile after 1 mile = $1.50

For any fraction of a mile , we round it up to the next mile and then take the following steps ( for example , for 0.6 miles , we take number of miles , x = 1) :

So , for x miles , we take ceiling of x = $\lceil x\rceil$ .

Cost for 0 miles =$0.

So, for x miles , we have extra charges will be applied on $\lceil x\rceil -1;x\ne 0$ miles.

Cost of cab for x miles = $f(x)=\{\begin{array}{l}0;x=0\\ 3+1.5(\lceil x\rceil -1);x>0\end{array}$

So, we have ,

Cost , $f(x)=\{\begin{array}{l}0;x=0\\ 3+1.5(\lceil x\rceil -1);x>0\end{array}$

where x = the number of miles( $\ge 0$ ).

We make a table for different number of miles and Cost of cab trip :

Number of miles (x)	Rounded up value = $\lceil x\rceil$	$\lceil x\rceil -1;x>0$	$f(x)=\{\begin{array}{l}0;x=0\\ 3+1.5(\lceil x\rceil -1);x>0\end{array}$
0	0	-	0
0.5	1	0	3
1	1	0	3
1.5	2	1	4.5
2	2	1	4.5
2.5	3	2	6
3	3	2	6

Graph:

From the table above , we draw the graph of the function :

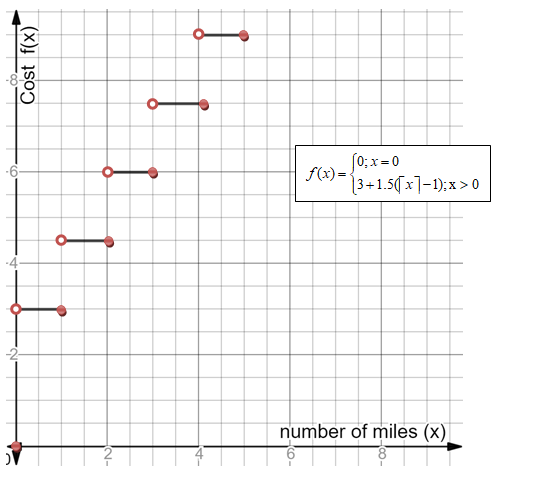
  $f(x)=\{\begin{array}{l}0;x=0\\ 3+1.5(\lceil x\rceil -1);x>0\end{array}$

  

(b)

To determine

To Calculate :

The cost if the trip is 8.5 miles long.

Answer to Problem 15PPS

The cost if the trip is 8.5 miles long = $15 .

Explanation of Solution

Given Information:

From part (a)

Cost of cab for x miles =

  $f(x)=\{\begin{array}{l}0;x=0\\ 3+1.5(\lceil x\rceil -1);x>0\end{array}\mathrm{....................}(1)$

Calculation:

Number of miles =8.5

Substituting x = 8.5 in equation (1)

  $\begin{array}{l}f(x)=\{\begin{array}{l}0;x=0\\ 3+1.5(\lceil x\rceil -1);x>0\end{array}\mathrm{....................}(1)\\ f(8.5)=3+1.5(\lceil 8.5\rceil -1)\mathrm{............................}[x=8.5]\\ f(8.5)=3+1.5(9-1)\mathrm{..................................}[simplify]\\ f(8.5)=3+1.5(8)\mathrm{.......................................}[simplify]\\ f(8.5)=3+\mathrm{12............................................}[simplify]\\ f(8.5)=\mathrm{15.................................................}[simplify]\end{array}$

Hence, the cost if trip is 8.5 miles long = $15.