Chapter 4, Problem 47P

To determine

Part (a) To Determine:

The acceleration of the system of crates.

Answer to Problem 47P

Solution:

The acceleration of the system is 1.7 m/s².

Explanation of Solution

Both the crates A and B are in contact with each other. Therefore, both the crates experience the same acceleration due to the force F acting on them.

The free body diagram of the crates is shown below.

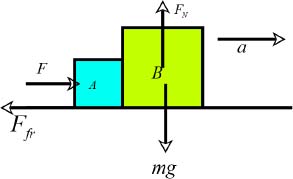
The mass m is the sum of the masses m_A and m_B of the crates. The weight mg of the system acts downwards, while the surface on which they rest exerts a normal force on the crates. Since the crates are accelerating, the force of kinetic friction acts on them.

For vertical equilibrium,

    $F_N=mg$ …………(1)

In the horizontal direction, the crates accelerate with an acceleration of a.

    $F-F_{fr}=ma$…………(2)

The force of kinetic friction is related to the normal force as,

    $F_{fr}={\mu }_k{F}_N$…………(3)

Equations (1), (2)and (3)can be simplified to give the expression for a.

    $a=\frac{F-F_{fr}}{m}=\frac{F-{\mu }_{k}mg}{m}$

Given:

The mass of crate A$m_A=65\text{ kg}$

The mass of crate B$m_B=125\text{ kg}$

The coefficient of kinetic friction ${\mu }_k=0.18$

Formula used:

$a=\frac{F-{\mu }_{k}mg}{m}$

Calculation:

Calculate the acceleration of the system by substituting the given values of mass, force, and coefficient of kinetic friction. Use 9.8 m/s² for g.

The mass of the system is the sum of the masses of the bodies A and B.

    $\begin{array}{c}m=m_A+m_B\end{array}$

        $\begin{array}{c}=65\text{ kg}+125\text{ kg}\end{array}$

        $\begin{array}{c}=190\text{ kg}\end{array}$

Calculate the acceleration of the system.

    $\begin{array}{c}a=\frac{F-{\mu }_{k}mg}{m}\end{array}$

        $\begin{array}{c}=\frac{\left(650\text{ N}\right)-\left(0.18\right)\left(190\text{ kg}\right)\left(9.8{\text{ m s}}^{-2}\right)}{\left(190\text{ kg}\right)}\end{array}$

        $\begin{array}{c}=1.657{\text{ m s}}^{-2}\end{array}$

To determine

Part (b) To Determine:

The force exerted by each crate on the other.

Answer to Problem 47P

Solution:

The force the crates exert on each other is 430 N.

Explanation of Solution

To calculate the force exerted by one body on the other, draw free body diagrams for A and B.

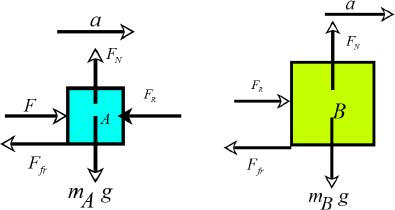
The crates exert a reaction force $F_R$ on each other.

For the crate B, the equation for horizontal motion can be written as,

    $F_R-{\left(F_{fr}\right)}_B=m_{B}a$

The force of kinetic friction for B is given by,

    ${\left(F_{fr}\right)}_B={\mu }_k{m}_{B}g$

The reaction force can be written as,

    $\begin{array}{c}{F}_R={\left(F_{fr}\right)}_B+m_{B}a\end{array}$

        $\begin{array}{c}={\mu }_k{m}_{B}g+m_{B}a\end{array}$

        $\begin{array}{c}=m_B\left({\mu }_{k}g+a\right)\end{array}$

Given:

The mass of crate A$m_A=65\text{ kg}$

The mass of crate B$m_B=125\text{ kg}$

The coefficient of kinetic friction ${\mu }_k=0.18$

Formula used:

$F_R=m_B\left({\mu }_{k}g+a\right)$

Calculation:

Use the given values in the equation $F_R=m_B\left({\mu }_{k}g+a\right)$ to determine the force exerted by one crate on the other.

    $\begin{array}{c}{F}_R=m_B\left({\mu }_{k}g+a\right)\end{array}$

        $\begin{array}{c}=\left(125\text{ kg}\right)\left[\left(0.18\right)\left(9.8{\text{ m s}}^{-2}\right)+\left(1.7{\text{ m/s}}^2\right)\right]\end{array}$

        $\begin{array}{c}=433\text{ N}\end{array}$

To determine

Part (c) To Determine:

The acceleration of the system and the force they exert on each other when the crates are reversed.

Answer to Problem 47P

Solution:

When the position of the crates is reversed, the acceleration is 1.7 m/s² and the force they exert on each other is 220 N.

Explanation of Solution

When the positions of the crates are reversed, the acceleration remains the same, since acceleration depends on the mass of the system.

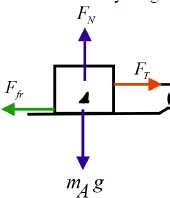
Draw the free body diagram for A.

For the crate A, the equation for horizontal motion can be written as,

$F_R-{\left(F_{fr}\right)}_A=m_{A}a$

The force of kinetic friction for A is given by,

    ${\left(F_{fr}\right)}_A={\mu }_k{m}_{A}g$

The reaction force can be written as,

    $\begin{array}{c}{F}_R={\left(F_{fr}\right)}_A+m_{A}a\end{array}$

        $\begin{array}{c}={\mu }_k{m}_{A}g+m_{A}a\end{array}$

        $\begin{array}{c}=m_A\left({\mu }_{k}g+a\right)\end{array}$

Given:

The mass of crate A$m_A=65\text{ kg}$

The mass of crate B$m_B=125\text{ kg}$

The coefficient of kinetic friction ${\mu }_k=0.18$

Formula used:

$a=\frac{F-{\mu }_{k}mg}{m}$$F_R=m_A\left({\mu }_{k}g+a\right)$

Calculation:

If the crates are reversed, the acceleration remains the same at 1.7 m/s².

The force exerted by one crate on the other when the position of the crates is reversed is calculated using the formula $F_R=m_A\left({\mu }_{k}g+a\right)$.

Substitute the given quantities in the equation.

    $\begin{array}{c}{F}_R=m_A\left({\mu }_{k}g+a\right)\end{array}$

        $\begin{array}{c}=\left(65\text{ kg}\right)\left[\left(0.18\right)\left(9.8{\text{ m s}}^{-2}\right)+\left(1.7{\text{ m/s}}^2\right)\right]\end{array}$

        $\begin{array}{c}=225.16\text{ N}\end{array}$