
Concept explainers
Consider the uniformly loaded simply supported steel beam with an overhang as shown. The second-area moment of the beam is I = 0.05 in4. Use superposition (with Table A–9 and the results of Prob. 4–20) to determine the reactions and the deflection equations of the beam. Plot the deflections.
Problem 4–21
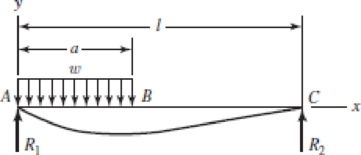
The net reaction at
The net reaction at
The expression for the deflection in the beam of portion
The expression for the deflection in the beam of portion
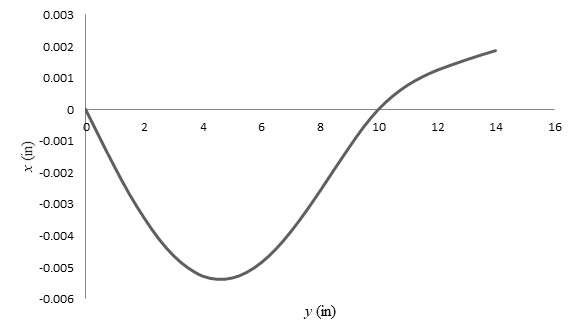
The plot of deflection verses length of the beam.
Answer to Problem 21P
The net reaction at
The net reaction at
The expression for the deflection in the beam of portion
The expression for the deflection in the beam of portion
The plot of deflection verses length of the beam is
Explanation of Solution
Write the expression for the reaction at
Here, the uniform load on the beam is
Write the expression for the reaction at
Here, the reaction at the
Write the expression for the deflection of the beam between
Here, the moment of inertia of the beam is
Write the expression for the slope of the deflection in the beam.
Substitute
Substitute
Write the expression for the deflection of the beam for
Substitute
Write the expression for the reaction at one end of the overhang section.
Here, the distance between
Write the expression for the reaction at other end of the overhang section.
Write the expression for the deflection in the beam section
Write the expression for the deflection in the beam section
Write the expression for the net reaction at
Write the expression for the net reaction at
Add equation (III) and (XI).
Add equation (VII) and (XII).
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Thus, the net reaction at
Substitute
Thus, the net reaction at
Substitute
Thus, the expression for the deflection in the beam of portion
Substitute
Thus, the expression for the deflection in the beam of portion
Substitute different values of
Substitute
Substitute
Similarly,
Use excel spread sheet to calculate the
The Table-(1) shows the different values of the deflection at different point of the beam.
Table-(1)
| S. No. | length | deflection |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 | ||
| 25 | ||
| 26 | ||
| 27 | ||
| 28 | ||
| 29 |
Draw the plot of length of the beam verses deflection of the beam.

Figure-(1)
Want to see more full solutions like this?
Chapter 4 Solutions
Shigley's Mechanical Engineering Design (McGraw-Hill Series in Mechanical Engineering)
- Figures 4: show a pneumatic controller. The pneumatic relay has the characteristic that pc=K pb , where K>0. What kind of control action does this controller produce? a. Derive the mathematical model for the system b. Derive the transfer function Pc(s)/E(s) -Solve step by step Orifice F+Ph R₁ Actuating error signal Flapper Nozzle. x+x F+Pe thinkarrow_forwardThe equation of the turning moment diagram for the three crank engine and the equation of the moment required by a machine connected to this engine are given below: Engine Torque Machine Torque T=10000-500 sin (40) T=10000+2000 sin (20) N.m N.m where radians is the crank angle from inner dead center and the mean engine speed is 300 rpm. It is required to select a proper flywheel (find the moment of inertia of the flywheel in kgm2) and then calculate the power of the engine if the total percentage fluctuation of speed of the flywheel is ±1% of the mean speed. Calculate the angular acceleration of the flywheel when angle is 45°.arrow_forwardDesign a cotter joint to support a axial load of 100kN . Carbon steel material selected whichhas Tensile stress = 100MPa Compressive stress =150MPa; Shear stress =60MPaarrow_forward
- Design a cotter joint to support a axial load of 100kN . Carbon steel material selected whichhas Tensile stress = 100MPa Compressive stress =150MPa; Shear stress =60MPaarrow_forwardI need all the derivations from Bohr's postulates in handwritten formarrow_forward12. Figure Q12 shows a prospective design for a conveyor roller system, for transferring crates, one at a time. The system is made up of two parallel rectangular steel beams, built-in at one end and simply supported at the other, with closely spaced rollers mounted in-between, for the crate to pass over. a) Using Macaulay notation, carry out an analysis of the problem and calculate the deflection of the mid-length point of the beams when the crate is centrally located, midway between A and B. State any important assumptions used in your analysis. [20 marks] b) Comment briefly whether this would be the maximum deflection of the beams when the crate is centrally located. 2 m 8 m A Direction of travel Figure Q12 (side view, only one beam visible) Useful information I for each separate beam = 12 ×10 m² E for both beams = 210 GPa Weight of one crate = 800 N [5 marks] Barrow_forward
- 11. A ring (side view shown in Figure Q11) has a circular solid cross-section of 5 mm diameter. The ring itself has a radius of R = 100 mm and a very narrow gap at point A, that allows the two free ends to be pulled apart by forces P, increasing the size of the gap. ○ P A Figure Q11 P a) Show that the total strain energy of the ring due to the applied forces is: U = 3πP²R³ 2EI [12 marks] b) Find the maximum bending stress produced if forces of P = 8 N are applied. [6 marks] c) What minimum force P would cause the material in the ring to yield and at which locations could this yielding begin to occur? Useful information E for the ring material = 75 GPa Oyield for the ring material = 190 MPa [7 marks]arrow_forwardQ2(15 Marks): From Fig. 2, Determine (a) mass equivalent in term x2, (b) stiffness equivalent in term x2, and (c) the natural frequency for the system in term x2. Note: (1) J Cylinder = mcr? J link (2) 2 3 Pulley, mass moment of inertia J Rigid link 1 (mass m₁), rotates with pulley. about O Cylinder, mass m Adherence to the symbols as in the question 152 153 xx(1) Fig. (2) m k₁ nimmunizmu Rigid link 2 (mass m₂)arrow_forwardQ3-B (7 Marks): A mass (m) is suspended from a spring of stiffness 4000 N/m and is subjected to a harmonic force having an amplitude of 100 N and a frequency of 5 Hz. The amplitude of the forced motion of the mass is observed to be 20 mm. Find the value of mass (m).arrow_forward
- Fig. (2) Q3-A (8 Marks): An automobile is modeled as a single-degree-of-freedom system vibrating in the vertical direction. It is driven along a road whose elevation varies sinusoidally. The distance from peak to trough is 0.2 m and the distance along the road between the peaks is 35 m. If the natural frequency of the automobile is 2 Hz and the damping ratio of the shock absorbers is 0.15, determine the amplitude of vibration of the automobile at a speed of 60 km/hour 6.18arrow_forward2. Q4(15 Marks): The motor-pump system shown in Fig. 4. is modeled as a rigid bar of mass m=50 kg and mass moment of inertia Jo=100 kg-m. The foundation of the system can be replaced by two springs of stiffness k=500 N/m and k₂-200 N/m and L=1 m. Determine the natural frequencies of the system. Motor, Fig. (4) 1 6(1) Pump C.G. x(1) x₁(1) Base (a) Foundation (b) C.G. m, Jo x2(1)arrow_forwardQ5(15 marks): Two equal pendulum free to rotate counterclockwise about the x-x axis are couple together by a rubber hose of torsional stiffness K lb.in/rad.as shown in Fig.5. determine the natural frequencies and mode shape for the normal modes of vibration. If L=19.3 in., W=3.86 lb, and k=20 lb.in/rad. Note: J=mL2 X (1) m 2 mc² 2 Xarrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
