Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015

1st Edition

ISBN: 9781680331165

Author: HOUGHTON MIFFLIN HARCOURT

Publisher: Houghton Mifflin Harcourt

See similar textbooks

Videos

Question

Chapter 3.5, Problem 57E

(a)

To determine

To determine: The possible solutions of a system of one quadratic equation and one equation of a circle.

(a)

Expert Solution

Answer to Problem 57E

A quadratic equation and a circle equation can have 0, 1, 2, 3 and 4 solutions.

Explanation of Solution

Calculation:

Consider the quadratic equation be y=ax2+bx+c

And the equation of a circle be (x−h)2+(y−k)2=r2

Graph 1:

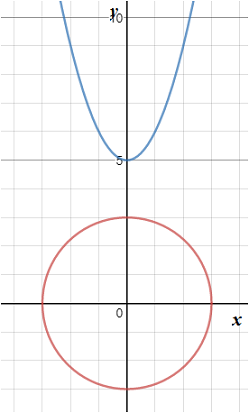
Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 1

In the above graph, it is seen that a quadratic equation that is, a parabola and a circle equation can intersect at no point.

Graph 2:

Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 2

In the above graph, it is seen that a quadratic equation that is, a parabola and a circle equation can intersect at one point.

Graph 3:

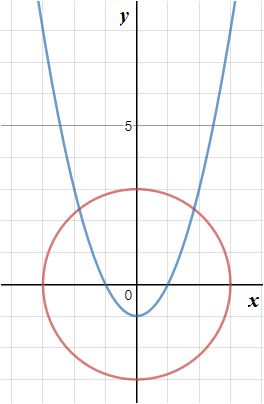
Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 3

In the above graph, it is seen that a quadratic equation that is, a parabola and a circle equation can intersect at two points.

Graph 4:

Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 4

In the above graph, it is seen that a quadratic equation that is, a parabola and a circle equation can intersect at three points.

Graph 5:

Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 5

In the above graph, it is seen that a quadratic equation that is, a parabola and a circle equation can intersect at four points.

Hence, a quadratic equation and a circle equation can have 0, 1, 2, 3 and 4 solutions.

(b)

To determine

To determine: The possible solutions of a system of two equations of circles.

(b)

Expert Solution

Answer to Problem 57E

Two equations of circles can have 0, 1, 2, and infinite number of solutions.

Explanation of Solution

Calculation:

Consider the system of two equations of circles be

{(x−h1)2+(y−k1)2=r12(x−h2)2+(y−k2)2=r22

Graph 1:

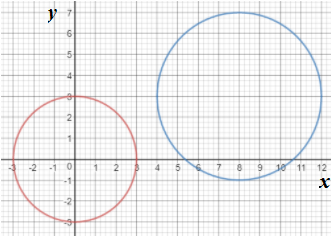
Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 6

In the above graph, it is seen that two equations of circles can intersect at no point.

Graph 2:

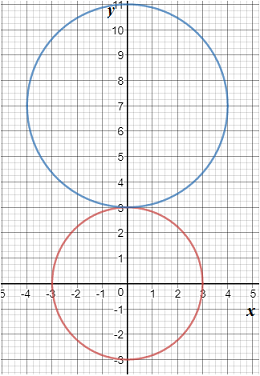
Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 7

In the above graph, it is seen that two equations of circles can intersect at one point.

Graph 3:

Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 8

In the above graph, it is seen that two equations of circles can intersect at two points.

Graph 4:

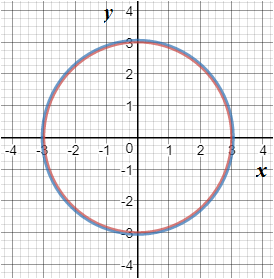
Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015, Chapter 3.5, Problem 57E , additional homework tip 9

In the above graph, it is seen that two equations of circles can intersect at infinite points.

Hence, two equations of circles can have 0, 1, 2, and infinite number of solutions.

Chapter 3.5, Problem 56E

Chapter 3.5, Problem 58E

Chapter 3 Solutions

Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015

Ch. 3.1 - Prob. 1E Ch. 3.1 - Prob. 2E Ch. 3.1 - Prob. 3E Ch. 3.1 - Prob. 4E Ch. 3.1 - Prob. 5E Ch. 3.1 - Prob. 6E Ch. 3.1 - Prob. 7E Ch. 3.1 - Prob. 8E Ch. 3.1 - Prob. 9E Ch. 3.1 - Prob. 10E

Ch. 3.1 - Prob. 11E Ch. 3.1 - Prob. 12E Ch. 3.1 - Prob. 13E Ch. 3.1 - Prob. 14E Ch. 3.1 - Prob. 15E Ch. 3.1 - Prob. 16E Ch. 3.1 - Prob. 17E Ch. 3.1 - Prob. 18E Ch. 3.1 - Prob. 19E Ch. 3.1 - Prob. 20E Ch. 3.1 - Prob. 21E Ch. 3.1 - Prob. 22E Ch. 3.1 - Prob. 23E Ch. 3.1 - Prob. 24E Ch. 3.1 - Prob. 25E Ch. 3.1 - Prob. 26E Ch. 3.1 - Prob. 27E Ch. 3.1 - Prob. 28E Ch. 3.1 - Prob. 29E Ch. 3.1 - Prob. 30E Ch. 3.1 - Prob. 31E Ch. 3.1 - Prob. 32E Ch. 3.1 - Prob. 33E Ch. 3.1 - Prob. 34E Ch. 3.1 - Prob. 35E Ch. 3.1 - Prob. 36E Ch. 3.1 - Prob. 37E Ch. 3.1 - Prob. 38E Ch. 3.1 - Prob. 39E Ch. 3.1 - Prob. 40E Ch. 3.1 - Prob. 41E Ch. 3.1 - Prob. 42E Ch. 3.1 - Prob. 43E Ch. 3.1 - Prob. 44E Ch. 3.1 - Prob. 45E Ch. 3.1 - Prob. 46E Ch. 3.1 - Prob. 47E Ch. 3.1 - Prob. 48E Ch. 3.1 - Prob. 49E Ch. 3.1 - Prob. 50E Ch. 3.1 - Prob. 51E Ch. 3.1 - Prob. 52E Ch. 3.1 - Prob. 53E Ch. 3.1 - Prob. 54E Ch. 3.1 - Prob. 55E Ch. 3.1 - Prob. 56E Ch. 3.1 - Prob. 57E Ch. 3.1 - Prob. 58E Ch. 3.1 - Prob. 59E Ch. 3.1 - Prob. 60E Ch. 3.1 - Prob. 61E Ch. 3.1 - Prob. 62E Ch. 3.1 - Prob. 63E Ch. 3.1 - Prob. 64E Ch. 3.1 - Prob. 65E Ch. 3.1 - Prob. 66E Ch. 3.1 - Prob. 67E Ch. 3.1 - Prob. 68E Ch. 3.1 - Prob. 69E Ch. 3.1 - Prob. 70E Ch. 3.1 - Prob. 71E Ch. 3.1 - Prob. 72E Ch. 3.1 - Prob. 73E Ch. 3.1 - Prob. 74E Ch. 3.1 - Prob. 75E Ch. 3.1 - Prob. 76E Ch. 3.1 - Prob. 77E Ch. 3.1 - Prob. 78E Ch. 3.1 - Prob. 79E Ch. 3.1 - Prob. 80E Ch. 3.1 - Prob. 81E Ch. 3.1 - Prob. 82E Ch. 3.1 - Prob. 83E Ch. 3.2 - Prob. 1E Ch. 3.2 - Prob. 2E Ch. 3.2 - Prob. 3E Ch. 3.2 - Prob. 4E Ch. 3.2 - Prob. 5E Ch. 3.2 - Prob. 6E Ch. 3.2 - Prob. 7E Ch. 3.2 - Prob. 8E Ch. 3.2 - Prob. 9E Ch. 3.2 - Prob. 10E Ch. 3.2 - Prob. 11E Ch. 3.2 - Prob. 12E Ch. 3.2 - Prob. 13E Ch. 3.2 - Prob. 14E Ch. 3.2 - Prob. 15E Ch. 3.2 - Prob. 16E Ch. 3.2 - Prob. 17E Ch. 3.2 - Prob. 18E Ch. 3.2 - Prob. 19E Ch. 3.2 - Prob. 20E Ch. 3.2 - Prob. 21E Ch. 3.2 - Prob. 22E Ch. 3.2 - Prob. 23E Ch. 3.2 - Prob. 24E Ch. 3.2 - Prob. 25E Ch. 3.2 - Prob. 26E Ch. 3.2 - Prob. 27E Ch. 3.2 - Prob. 28E Ch. 3.2 - Prob. 29E Ch. 3.2 - Prob. 30E Ch. 3.2 - Prob. 31E Ch. 3.2 - Prob. 32E Ch. 3.2 - Prob. 33E Ch. 3.2 - Prob. 34E Ch. 3.2 - Prob. 35E Ch. 3.2 - Prob. 36E Ch. 3.2 - Prob. 37E Ch. 3.2 - Prob. 38E Ch. 3.2 - Prob. 39E Ch. 3.2 - Prob. 40E Ch. 3.2 - Prob. 41E Ch. 3.2 - Prob. 42E Ch. 3.2 - Prob. 43E Ch. 3.2 - Prob. 44E Ch. 3.2 - Prob. 45E Ch. 3.2 - Prob. 46E Ch. 3.2 - Prob. 47E Ch. 3.2 - Prob. 48E Ch. 3.2 - Prob. 49E Ch. 3.2 - Prob. 50E Ch. 3.2 - Prob. 51E Ch. 3.2 - Prob. 52E Ch. 3.2 - Prob. 53E Ch. 3.2 - Prob. 54E Ch. 3.2 - Prob. 55E Ch. 3.2 - Prob. 56E Ch. 3.2 - Prob. 57E Ch. 3.2 - Prob. 58E Ch. 3.2 - Prob. 59E Ch. 3.2 - Prob. 60E Ch. 3.2 - Prob. 61E Ch. 3.2 - Prob. 62E Ch. 3.2 - Prob. 63E Ch. 3.2 - Prob. 64E Ch. 3.2 - Prob. 65E Ch. 3.2 - Prob. 66E Ch. 3.2 - Prob. 67E Ch. 3.2 - Prob. 68E Ch. 3.2 - Prob. 69E Ch. 3.2 - Prob. 70E Ch. 3.2 - Prob. 71E Ch. 3.2 - Prob. 72E Ch. 3.2 - Prob. 73E Ch. 3.2 - Prob. 74E Ch. 3.2 - Prob. 75E Ch. 3.2 - Prob. 76E Ch. 3.2 - Prob. 77E Ch. 3.2 - Prob. 78E Ch. 3.2 - Prob. 79E Ch. 3.2 - Prob. 80E Ch. 3.2 - Prob. 81E Ch. 3.2 - Prob. 82E Ch. 3.2 - Prob. 83E Ch. 3.2 - Prob. 84E Ch. 3.3 - Prob. 1E Ch. 3.3 - Prob. 2E Ch. 3.3 - Prob. 3E Ch. 3.3 - Prob. 4E Ch. 3.3 - Prob. 5E Ch. 3.3 - Prob. 6E Ch. 3.3 - Prob. 7E Ch. 3.3 - Prob. 8E Ch. 3.3 - Prob. 9E Ch. 3.3 - Prob. 10E Ch. 3.3 - Prob. 11E Ch. 3.3 - Prob. 12E Ch. 3.3 - Prob. 13E Ch. 3.3 - Prob. 14E Ch. 3.3 - Prob. 15E Ch. 3.3 - Prob. 16E Ch. 3.3 - Prob. 17E Ch. 3.3 - Prob. 18E Ch. 3.3 - Prob. 19E Ch. 3.3 - Prob. 20E Ch. 3.3 - Prob. 21E Ch. 3.3 - Prob. 22E Ch. 3.3 - Prob. 23E Ch. 3.3 - Prob. 24E Ch. 3.3 - Prob. 25E Ch. 3.3 - Prob. 26E Ch. 3.3 - Prob. 27E Ch. 3.3 - Prob. 28E Ch. 3.3 - Prob. 29E Ch. 3.3 - Prob. 30E Ch. 3.3 - Prob. 31E Ch. 3.3 - Prob. 32E Ch. 3.3 - Prob. 33E Ch. 3.3 - Prob. 34E Ch. 3.3 - Prob. 35E Ch. 3.3 - Prob. 36E Ch. 3.3 - Prob. 37E Ch. 3.3 - Prob. 38E Ch. 3.3 - Prob. 39E Ch. 3.3 - Prob. 40E Ch. 3.3 - Prob. 41E Ch. 3.3 - Prob. 42E Ch. 3.3 - Prob. 43E Ch. 3.3 - Prob. 44E Ch. 3.3 - Prob. 45E Ch. 3.3 - Prob. 46E Ch. 3.3 - Prob. 47E Ch. 3.3 - Prob. 48E Ch. 3.3 - Prob. 49E Ch. 3.3 - Prob. 50E Ch. 3.3 - Prob. 51E Ch. 3.3 - Prob. 52E Ch. 3.3 - Prob. 53E Ch. 3.3 - Prob. 54E Ch. 3.3 - Prob. 55E Ch. 3.3 - Prob. 56E Ch. 3.3 - Prob. 57E Ch. 3.3 - Prob. 58E Ch. 3.3 - Prob. 59E Ch. 3.3 - Prob. 60E Ch. 3.3 - Prob. 61E Ch. 3.3 - Prob. 62E Ch. 3.3 - Prob. 63E Ch. 3.3 - Prob. 64E Ch. 3.3 - Prob. 65E Ch. 3.3 - Prob. 66E Ch. 3.3 - Prob. 67E Ch. 3.3 - Prob. 68E Ch. 3.3 - Prob. 69E Ch. 3.3 - Prob. 70E Ch. 3.3 - Prob. 71E Ch. 3.3 - Prob. 72E Ch. 3.3 - Prob. 73E Ch. 3.3 - Prob. 74E Ch. 3.3 - Prob. 75E Ch. 3.3 - Prob. 76E Ch. 3.3 - Prob. 77E Ch. 3.3 - Prob. 78E Ch. 3.3 - Prob. 79E Ch. 3.3 - Prob. 80E Ch. 3.3 - Prob. 81E Ch. 3.3 - Prob. 1Q Ch. 3.3 - Prob. 2Q Ch. 3.3 - Prob. 3Q Ch. 3.3 - Prob. 4Q Ch. 3.3 - Prob. 5Q Ch. 3.3 - Prob. 6Q Ch. 3.3 - Prob. 7Q Ch. 3.3 - Prob. 8Q Ch. 3.3 - Prob. 9Q Ch. 3.3 - Prob. 10Q Ch. 3.3 - Prob. 11Q Ch. 3.3 - Prob. 12Q Ch. 3.3 - Prob. 13Q Ch. 3.3 - Prob. 14Q Ch. 3.3 - Prob. 15Q Ch. 3.3 - Prob. 16Q Ch. 3.3 - Prob. 17Q Ch. 3.3 - Prob. 18Q Ch. 3.4 - Prob. 1E Ch. 3.4 - Prob. 2E Ch. 3.4 - Prob. 3E Ch. 3.4 - Prob. 4E Ch. 3.4 - Prob. 5E Ch. 3.4 - Prob. 6E Ch. 3.4 - Prob. 7E Ch. 3.4 - Prob. 8E Ch. 3.4 - Prob. 9E Ch. 3.4 - Prob. 10E Ch. 3.4 - Prob. 11E Ch. 3.4 - Prob. 12E Ch. 3.4 - Prob. 13E Ch. 3.4 - Prob. 14E Ch. 3.4 - Prob. 15E Ch. 3.4 - Prob. 16E Ch. 3.4 - Prob. 17E Ch. 3.4 - Prob. 18E Ch. 3.4 - Prob. 19E Ch. 3.4 - Prob. 20E Ch. 3.4 - Prob. 21E Ch. 3.4 - Prob. 22E Ch. 3.4 - Prob. 23E Ch. 3.4 - Prob. 24E Ch. 3.4 - Prob. 25E Ch. 3.4 - Prob. 26E Ch. 3.4 - Prob. 27E Ch. 3.4 - Prob. 28E Ch. 3.4 - Prob. 29E Ch. 3.4 - Prob. 30E Ch. 3.4 - Prob. 31E Ch. 3.4 - Prob. 32E Ch. 3.4 - Prob. 33E Ch. 3.4 - Prob. 34E Ch. 3.4 - Prob. 35E Ch. 3.4 - Prob. 36E Ch. 3.4 - Prob. 37E Ch. 3.4 - Prob. 38E Ch. 3.4 - Prob. 39E Ch. 3.4 - Prob. 40E Ch. 3.4 - Prob. 41E Ch. 3.4 - Prob. 42E Ch. 3.4 - Prob. 43E Ch. 3.4 - Prob. 44E Ch. 3.4 - Prob. 45E Ch. 3.4 - Prob. 46E Ch. 3.4 - Prob. 47E Ch. 3.4 - Prob. 48E Ch. 3.4 - Prob. 49E Ch. 3.4 - Prob. 50E Ch. 3.4 - Prob. 51E Ch. 3.4 - Prob. 52E Ch. 3.4 - Prob. 53E Ch. 3.4 - Prob. 54E Ch. 3.4 - Prob. 55E Ch. 3.4 - Prob. 56E Ch. 3.4 - Prob. 57E Ch. 3.4 - Prob. 58E Ch. 3.4 - Prob. 59E Ch. 3.4 - Prob. 60E Ch. 3.4 - Prob. 61E Ch. 3.4 - Prob. 62E Ch. 3.4 - Prob. 63E Ch. 3.4 - Prob. 64E Ch. 3.4 - Prob. 65E Ch. 3.4 - Prob. 66E Ch. 3.4 - Prob. 67E Ch. 3.4 - Prob. 68E Ch. 3.4 - Prob. 69E Ch. 3.4 - Prob. 70E Ch. 3.4 - Prob. 71E Ch. 3.4 - Prob. 72E Ch. 3.4 - Prob. 73E Ch. 3.4 - Prob. 74E Ch. 3.4 - Prob. 75E Ch. 3.4 - Prob. 76E Ch. 3.4 - Prob. 77E Ch. 3.4 - Prob. 78E Ch. 3.4 - Prob. 79E Ch. 3.4 - Prob. 80E Ch. 3.4 - Prob. 81E Ch. 3.4 - Prob. 82E Ch. 3.4 - Prob. 83E Ch. 3.4 - Prob. 84E Ch. 3.5 - Prob. 1E Ch. 3.5 - Prob. 2E Ch. 3.5 - Prob. 3E Ch. 3.5 - Prob. 4E Ch. 3.5 - Prob. 5E Ch. 3.5 - Prob. 6E Ch. 3.5 - Prob. 7E Ch. 3.5 - Prob. 8E Ch. 3.5 - Prob. 9E Ch. 3.5 - Prob. 10E Ch. 3.5 - Prob. 11E Ch. 3.5 - Prob. 12E Ch. 3.5 - Prob. 13E Ch. 3.5 - Prob. 14E Ch. 3.5 - Prob. 15E Ch. 3.5 - Prob. 16E Ch. 3.5 - Prob. 17E Ch. 3.5 - Prob. 18E Ch. 3.5 - Prob. 19E Ch. 3.5 - Prob. 20E Ch. 3.5 - Prob. 21E Ch. 3.5 - Prob. 22E Ch. 3.5 - Prob. 23E Ch. 3.5 - Prob. 24E Ch. 3.5 - Prob. 25E Ch. 3.5 - Prob. 26E Ch. 3.5 - Prob. 27E Ch. 3.5 - Prob. 28E Ch. 3.5 - Prob. 29E Ch. 3.5 - Prob. 30E Ch. 3.5 - Prob. 31E Ch. 3.5 - Prob. 32E Ch. 3.5 - Prob. 33E Ch. 3.5 - Prob. 34E Ch. 3.5 - Prob. 35E Ch. 3.5 - Prob. 36E Ch. 3.5 - Prob. 37E Ch. 3.5 - Prob. 38E Ch. 3.5 - Prob. 39E Ch. 3.5 - Prob. 40E Ch. 3.5 - Prob. 41E Ch. 3.5 - Prob. 42E Ch. 3.5 - Prob. 43E Ch. 3.5 - Prob. 44E Ch. 3.5 - Prob. 45E Ch. 3.5 - Prob. 46E Ch. 3.5 - Prob. 47E Ch. 3.5 - Prob. 48E Ch. 3.5 - Prob. 49E Ch. 3.5 - Prob. 50E Ch. 3.5 - Prob. 51E Ch. 3.5 - Prob. 52E Ch. 3.5 - Prob. 53E Ch. 3.5 - Prob. 54E Ch. 3.5 - Prob. 55E Ch. 3.5 - Prob. 56E Ch. 3.5 - Prob. 57E Ch. 3.5 - Prob. 58E Ch. 3.5 - Prob. 59E Ch. 3.5 - Prob. 60E Ch. 3.5 - Prob. 61E Ch. 3.5 - Prob. 62E Ch. 3.5 - Prob. 63E Ch. 3.5 - Prob. 64E Ch. 3.5 - Prob. 65E Ch. 3.5 - Prob. 66E Ch. 3.6 - Prob. 1E Ch. 3.6 - Prob. 2E Ch. 3.6 - Prob. 3E Ch. 3.6 - Prob. 4E Ch. 3.6 - Prob. 5E Ch. 3.6 - Prob. 6E Ch. 3.6 - Prob. 7E Ch. 3.6 - Prob. 8E Ch. 3.6 - Prob. 9E Ch. 3.6 - Prob. 10E Ch. 3.6 - Prob. 11E Ch. 3.6 - Prob. 12E Ch. 3.6 - Prob. 13E Ch. 3.6 - Prob. 14E Ch. 3.6 - Prob. 15E Ch. 3.6 - Prob. 16E Ch. 3.6 - Prob. 17E Ch. 3.6 - Prob. 18E Ch. 3.6 - Prob. 19E Ch. 3.6 - Prob. 20E Ch. 3.6 - Prob. 21E Ch. 3.6 - Prob. 22E Ch. 3.6 - Prob. 23E Ch. 3.6 - Prob. 24E Ch. 3.6 - Prob. 25E Ch. 3.6 - Prob. 26E Ch. 3.6 - Prob. 27E Ch. 3.6 - Prob. 28E Ch. 3.6 - Prob. 29E Ch. 3.6 - Prob. 30E Ch. 3.6 - Prob. 31E Ch. 3.6 - Prob. 32E Ch. 3.6 - Prob. 33E Ch. 3.6 - Prob. 34E Ch. 3.6 - Prob. 35E Ch. 3.6 - Prob. 36E Ch. 3.6 - Prob. 37E Ch. 3.6 - Prob. 38E Ch. 3.6 - Prob. 39E Ch. 3.6 - Prob. 40E Ch. 3.6 - Prob. 41E Ch. 3.6 - Prob. 42E Ch. 3.6 - Prob. 43E Ch. 3.6 - Prob. 44E Ch. 3.6 - Prob. 45E Ch. 3.6 - Prob. 46E Ch. 3.6 - Prob. 47E Ch. 3.6 - Prob. 48E Ch. 3.6 - Prob. 49E Ch. 3.6 - Prob. 50E Ch. 3.6 - Prob. 51E Ch. 3.6 - Prob. 52E Ch. 3.6 - Prob. 53E Ch. 3.6 - Prob. 54E Ch. 3.6 - Prob. 55E Ch. 3.6 - Prob. 56E Ch. 3.6 - Prob. 57E Ch. 3.6 - Prob. 58E Ch. 3.6 - Prob. 59E Ch. 3.6 - Prob. 60E Ch. 3 - Prob. 1CR Ch. 3 - Prob. 2CR Ch. 3 - Prob. 3CR Ch. 3 - Prob. 4CR Ch. 3 - Prob. 5CR Ch. 3 - Prob. 6CR Ch. 3 - Prob. 7CR Ch. 3 - Prob. 8CR Ch. 3 - Prob. 9CR Ch. 3 - Prob. 10CR Ch. 3 - Prob. 11CR Ch. 3 - Prob. 12CR Ch. 3 - Prob. 13CR Ch. 3 - Prob. 14CR Ch. 3 - Prob. 15CR Ch. 3 - Prob. 16CR Ch. 3 - Prob. 17CR Ch. 3 - Prob. 18CR Ch. 3 - Prob. 19CR Ch. 3 - Prob. 20CR Ch. 3 - Prob. 21CR Ch. 3 - Prob. 22CR Ch. 3 - Prob. 23CR Ch. 3 - Prob. 24CR Ch. 3 - Prob. 25CR Ch. 3 - Prob. 26CR Ch. 3 - Prob. 27CR Ch. 3 - Prob. 28CR Ch. 3 - Prob. 29CR Ch. 3 - Prob. 30CR Ch. 3 - Prob. 31CR Ch. 3 - Prob. 32CR Ch. 3 - Prob. 33CR Ch. 3 - Prob. 34CR Ch. 3 - Prob. 35CR Ch. 3 - Prob. 1CT Ch. 3 - Prob. 2CT Ch. 3 - Prob. 3CT Ch. 3 - Prob. 4CT Ch. 3 - Prob. 5CT Ch. 3 - Prob. 6CT Ch. 3 - Prob. 7CT Ch. 3 - Prob. 8CT Ch. 3 - Prob. 9CT Ch. 3 - Prob. 10CT Ch. 3 - Prob. 11CT Ch. 3 - Prob. 12CT Ch. 3 - Prob. 13CT Ch. 3 - Prob. 14CT Ch. 3 - Prob. 1CA Ch. 3 - Prob. 2CA Ch. 3 - Prob. 3CA Ch. 3 - Prob. 4CA Ch. 3 - Prob. 5CA Ch. 3 - Prob. 6CA Ch. 3 - Prob. 7CA Ch. 3 - Prob. 8CA Ch. 3 - Prob. 9CA

Knowledge Booster

$Algebra$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education

Algebra and Trigonometry (6th Edition)

Algebra

ISBN:9780134463216

Author:Robert F. Blitzer

Publisher:PEARSON

Contemporary Abstract Algebra

Algebra

ISBN:9781305657960

Author:Joseph Gallian

Publisher:Cengage Learning

Linear Algebra: A Modern Introduction

Algebra

ISBN:9781285463247

Author:David Poole

Publisher:Cengage Learning

Algebra And Trigonometry (11th Edition)

Algebra

ISBN:9780135163078

Author:Michael Sullivan

Publisher:PEARSON

Introduction to Linear Algebra, Fifth Edition

Algebra

ISBN:9780980232776

Author:Gilbert Strang

Publisher:Wellesley-Cambridge Press

College Algebra (Collegiate Math)

Algebra

ISBN:9780077836344

Author:Julie Miller, Donna Gerken

Publisher:McGraw-Hill Education

SEE MORE TEXTBOOKS

Finite Math: Markov Chain Example - The Gambler's Ruin; Author: Brandon Foltz;https://www.youtube.com/watch?v=afIhgiHVnj0;License: Standard YouTube License, CC-BY

Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra; Author: AfterMath;https://www.youtube.com/watch?v=qK-PUTuUSpw;License: Standard Youtube License

Stochastic process and Markov Chain Model | Transition Probability Matrix (TPM); Author: Dr. Harish Garg;https://www.youtube.com/watch?v=sb4jo4P4ZLI;License: Standard YouTube License, CC-BY

The possible solutions of a system of one quadratic equation and one equation of a circle .

Videos

To determine: The possible solutions of a system of one quadratic equation and one equation of a circle.

Answer to Problem 57E

Explanation of Solution

To determine: The possible solutions of a system of two equations of circles.

Answer to Problem 57E

Explanation of Solution

Chapter 3 Solutions