Physics for Scientists and Engineers
10th Edition
ISBN: 9781337553278
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 33, Problem 47AP
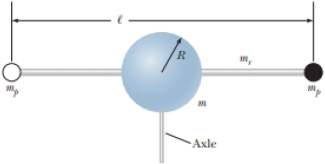
You are working at NASA, in a division that is studying the possibility of rotating small spacecraft using
Figure P33.47
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Assume the radiation from a heat lamp is monochromatic, with a wavelength of 1.5 μm . I =3.313 kW/m^2.
a. What is the peak electric field strength, in kilovolts per meter?
b. Find the peak magnetic field strength, in microtesla.
c. How long, in seconds, will it take to increase the temperature of the 3.95-kg shoulder by 2.00°C, assuming that the shoulder absorbs all the radiation from the lamp and given that its specific heat is 3.47 × 103 J/(kg⋅°C)?
The photon energies used in different types of medical x-ray imaging vary widely, depending upon the application. Single dental x rays use photons with energies of about 25 keV. The photon energy used for x-ray microtomography, a process that allows repeated imaging in single planes at varying depths within the sample, is 2.5 times greater. What are the wavelengths of the x rays used for these two purposes?
32. When you use Maxwell's equations to determine electric
and magnetic fields, a lot depends on making the “right"
choice for the integration path. What happens if you choose
the "wrong" path? Do the equations still hold? Consider a
parallel-plate capacitor with circular plates, but use a rectan-
gular integration path that has two sides parallel to the plates
and two sides perpendicular to them, as in Figure P30.32.
What do you get? •
Figure P30.32
- integration
path
Chapter 33 Solutions
Physics for Scientists and Engineers
Ch. 33.1 - Prob. 33.1QQCh. 33.3 - What is the phase difference between the...Ch. 33.3 - Prob. 33.3QQCh. 33.5 - Prob. 33.4QQCh. 33.6 - If the antenna in Figure 33.11 represents the...Ch. 33.7 - Prob. 33.6QQCh. 33.7 - A radio wave of frequency on the order of 105 Hz...Ch. 33 - Prob. 1PCh. 33 - Prob. 2PCh. 33 - A proton moves through a region containing a...
Ch. 33 - A diathermy machine, used in physiotherapy,...Ch. 33 - The distance to the North Star, Polaris, is...Ch. 33 - A radar pulse returns to the transmitterreceiver...Ch. 33 - The speed of an electromagnetic wave traveling in...Ch. 33 - You are working for SETI, the Search for...Ch. 33 - Review. A microwave oven is powered by a...Ch. 33 - Verify by substitution that the following...Ch. 33 - Why is the following situation impossible? An...Ch. 33 - At what distance from the Sun is the intensity of...Ch. 33 - If the intensity of sunlight at the Earths surface...Ch. 33 - Prob. 14PCh. 33 - High-power lasers in factories are used to cut...Ch. 33 - Review. Model the electromagnetic wave in a...Ch. 33 - Prob. 17PCh. 33 - Prob. 18PCh. 33 - Prob. 19PCh. 33 - Prob. 20PCh. 33 - A 25.0-mW laser beam of diameter 2.00 mm is...Ch. 33 - The intensity of sunlight at the Earths distance...Ch. 33 - Prob. 23PCh. 33 - Prob. 24PCh. 33 - Prob. 25PCh. 33 - Assume the intensity of solar radiation incident...Ch. 33 - Extremely low-frequency (ELF) waves that can...Ch. 33 - A large, flat sheet carries a uniformly...Ch. 33 - Prob. 29PCh. 33 - Prob. 30PCh. 33 - Prob. 31PCh. 33 - An important news announcement is transmitted by...Ch. 33 - Assume the intensity of solar radiation incident...Ch. 33 - Classify waves with frequencies of 2 Hz, 2 kHz, 2...Ch. 33 - The eye is most sensitive to light having a...Ch. 33 - Prob. 36APCh. 33 - You are working as a radio technician. One day,...Ch. 33 - One goal of the Russian space program is to...Ch. 33 - The intensity of solar radiation at the top of the...Ch. 33 - The Earth reflects approximately 38.0% of the...Ch. 33 - Consider a small, spherical particle of radius r...Ch. 33 - Consider a small, spherical particle of radius r...Ch. 33 - Review. A 1.00-m-diameter circular mirror focuses...Ch. 33 - Prob. 44APCh. 33 - Prob. 45APCh. 33 - You may wish to review Sections 16.4 and 16.8 on...Ch. 33 - You are working at NASA, in a division that is...Ch. 33 - Prob. 48APCh. 33 - Prob. 49APCh. 33 - Prob. 50CPCh. 33 - Prob. 51CP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A uniform circular disk of mass m = 24.0 g and radius r = 40.0 cm hangs vertically from a fixed, frictionless, horizontal hinge at a point on its circumference as shown in Figure P34.39a. A beam of electromagnetic radiation with intensity 10.0 MW/m2 is incident on the disk, in a direction perpendicular to its surface. The disk is perfectly absorbing, and the resulting radiation pressure makes the disk rotate. Assuming the radiation is always perpendicular to the surface of the disk, find the angle through which the disk rotates from the vertical as it reaches its new equilibrium position shown in Figure 34.39b. Figure 34.39arrow_forwardAn electromagnetic plane wave, that is propagating in the x-direction at a speed of 3.00 x108 m/s, has a peak electric field strength of 4,200 N/C and a wavelength of 900 nm. Which of the following functions represents the correct behavior for the magnetic field? a. B(x, t) = (21 µT)sin[(9.00 x 10-7 m-1)x – (2.09 x 1015 rad/s)t] b. B(x, t) = (28 µT)sin[(6.98 x 106 m-1)x – (2.09 x 1015 rad/s)t] c. B(x, t) = (14 µT)sin[(6.98 x 106 m-1)x – (2.09 x 1015 rad/s)t] d. B(x, t) = (14 µT)sin[(6.98 x 106 m-1)x – (3.14 x 1015 rad/s)t] e. B(x, t) = (4,200 µT)sin[(6.98 x 106 m-1)x – (2.09 x 1015 rad/s)t]arrow_forwardThe star Sirius is much hotter than the sun, with a peak wavelength of 290 nm compared to the sun’s 500 nm. It is also larger, with a diameter 1.7 times that of the sun. By what factor does the energy emitted by Sirius exceed that of the sun?arrow_forward
- The 2.0-cm-diameter solenoid shown passes through the center of a 6.0-cm-diameter loop. The magnetic field inside the solenoid is 0.20 T. What is the magnetic flux through the loop (a) when it is perpendicular to the solenoid and (b) when it is tilted at a 60° angle?arrow_forwardA laser can suspend a small glass sphere in Earth's gravitational field, g = 9.80 m/s2. Assume that the suspended sphere is made of perfectly absorbing black glass. The sphere has a radius of 0.560 mm and a density of 0.190 g/cm3. Determine the radiation intensity needed to keep the small glass sphere suspended. (answer in kW / cm^2)arrow_forwardA parabolic reflector focuses electromagnetic waves into a beam as shown in the figure. The electromagnetic radiation is pulsed, with a pulse frequency of 19.0 GHz, and the duration of each pulse is t = 1.00 ns. The face of the reflector has a radius of 3.00 cm, and the average power during each pulse is 29.0 kW. (Due to the nature of this problem, do not use rounded intermediate values in your calculations—including answers submitted in WebAssign.) (a) What is the wavelength (in cm) of these electromagnetic waves? (b) What is the total energy (in µJ) contained in each pulse? (c)Compute the average energy density (in mJ/m3) inside each pulse. (d)Determine the amplitude of the electric field (in kV/m) and magnetic field (in µT) in these electromagnetic waves. (e) Assuming that this pulsed beam strikes an absorbing surface, compute the force (in µN) exerted on the surface during the 1.00 ns duration of each pulse.arrow_forward
- A parabolic reflector focuses electromagnetic waves into a beam as shown in the figure. The electromagnetic radiation is pulsed, with a pulse frequency of 19.0 GHz, and the duration of each pulse is t = 1.00 ns. The face of the reflector has a radius of 3.00 cm, and the average power during each pulse is 29.0 kW. (Due to the nature of this problem, do not use rounded intermediate values in your calculations—including answers submitted in WebAssign.) (d) Determine the amplitude of the electric field (in kV/m) and magnetic field (in µT) in these electromagnetic waves. Emax= kV/m Bmax = µT (e) Assuming that this pulsed beam strikes an absorbing surface, compute the force (in µN) exerted on the surface during the 1.00 ns duration of each pulse. µNarrow_forwardInterplanetary space contains many small particles referred to as interplanetary dust. Radiation pressure from the sun sets a lower limit on the size of such dust particles. To see the origin of this limit, consider a spherical dust particle of radius R and mass density r. (a) Write an expression for the gravitational force exerted on this particle by the sun (mass M) when the particle is a distance r from the sun. (b) Let L represent the luminosity of the sun, equal to the rate at which it emits energy in electromagnetic radiation. Find the force exerted on the (totally absorbing) particle due to solar radiation pressure, remembering that the intensity of the sun’s radiation also depends on the distance r. The relevant area is the cross-sectional area of the particle, not the total surface area of the particle. As part of your answer, explain why this is so. (c) The mass density of a typical interplanetary dust particle is about 3000 kg/m3 . Find the particle radius R such that the…arrow_forwardYour friend bought a magnetic field sensor and convinced you to help him measure the magnetic field at a certain distance from your local radio station's antenna. The max magnetic field you measure is 2.1*10^-11 T and a quick Google search tells you that this particular station broadcasts at a frequency of 773 kHz. What is the max electric field in V/m of the emitted electromagnetic waves?arrow_forward
- Two z-oriented dipole antennas are located at x=-2 and x=2, respectively. We know that I₁l = 1₂l. In the xz plane, what is the smallest angle where the far field is null? I₁l -^ Z 0 s 1₂1 λ Fig. Q10 Xarrow_forwardSuppose you have an electric field as a result of superposition of two waves given by Ē(z, t) = Eo cos(kz - wt) + Eo cos(kz + wt)â. a. Simplify Ē(z, t) as one term and find its associated magnetic field b. Find the instantaneous and time-averaged energy density.arrow_forwardAn electromagnetic wave of wavelength 435nm is traveling in a vacuum in the -z-direction. The electric field has an amplitude 2.70×10^−3 V/m2.70×10−3V/m and is parallel to the x-axis. What is the frequency? Express your answer in hertz. What is the magnetic-field amplitude? Express your answer in teslas.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
What Are Electromagnetic Wave Properties? | Physics in Motion; Author: GPB Education;https://www.youtube.com/watch?v=ftyxZBxBexI;License: Standard YouTube License, CC-BY