
Concept explainers
To describe: The number of lines that can be drawn in space through the vertex of a
Answer to Problem 18CE
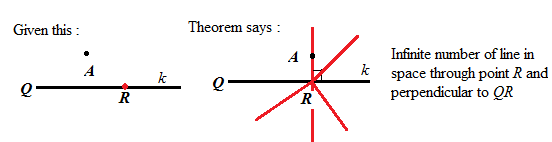
Through point R on the line
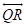 in space infinite number of lines like
in space infinite number of lines like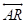 can be drawn perpendicular to
can be drawn perpendicular to 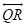
Explanation of Solution
Given information:
The lines drawn through point R in space perpendicular to side
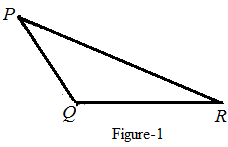
shown in Figure-1.
Theorem used:
In a plane, through a point outside a line, there is exactly one line perpendicular to the given line.
But in a space, through a point outside a line, there is exactly one line perpendicular to the given line.
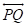
According to the theorem stated above, through the point R on the line
 infinite number of lines like
infinite number of lines like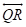 can be drawn perpendicular to
can be drawn perpendicular to 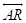
The theorem that justify the answer is stated as:
In a plane, through a point outside a line, there is exactly one line perpendicular to the given line.
Because, there are infinite number of planes containing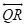
Conclusion:
Through point R on the line
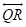 in space infinite number of lines like
in space infinite number of lines like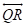 can be drawn perpendicular to
can be drawn perpendicular to 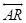
Chapter 3 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
Elementary Statistics: Picturing the World (7th Edition)
Introductory Statistics
College Algebra (7th Edition)
Pre-Algebra Student Edition
Elementary Statistics (13th Edition)
- Only 100% sure experts solve it correct complete solutions need to get full marks it's my quiz okkkk.take your time but solve full accurate okkk Geometry expert solve itarrow_forwardOnly 100% sure experts solve it correct complete solutions need to get full marks it's my quiz okkkk.take your time but solve full accurate okkk Geometry expert solve itarrow_forwardMinimum number of times that activity should be recorded: 9 (3 each phase) Sample calculation (Azimuth- Stars): On 05th May 2006 at 11h00m00s UTC, a vessel in position 04°30'N 010°00'W observed Canopus bearing 145° by compass. Find the compass error. If variation was 4.0° East, calculate the deviation. GHA Aries (05d 11h): 028° 10.7' Increment (00m 00s): 000° 00.0' GHA Aries: 028° 10.7' Longitude (W): (-) 010° 00.0' (minus- since longitude is westerly) LHA Aries: 018° 10.7' SHA Canopus: (+) 263° 59.0' LHA Canopus: 282° 09.7' S 052° 42.1' Declination: P=360-282° 09.7'= 77° 50.3' (If LHA>180°, P= 360-LHA) A Tan Latitude/ Tan P A Tan 04° 30' Tan 77° 50.3' A = 0.016960803 S (A is named opposite to latitude, except when hour angle is between 090° and 270°) B=Tan Declination/ Sin P B= Tan 052° 42.1/ Sin 77° 50.3' B=1.342905601 S (B is always named same as declination) C=A+B=1.359866404 S (C correction, A+/- B: If A and B have same name- add, If different name- subtract) Tan Azimuth 1/ (CX…arrow_forward
- 3) roadway Calculate the overall length of the conduit run sketched below. 2' Radius 8' 122-62 Sin 30° = 6/H 1309 16.4%. 12' H= 6/s in 30° Year 2 Exercise Book Page 4 10 10 10 fx-300MS S-V.PA Topic 1arrow_forwardWhat is a? And b?arrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Automobile Department Subject :Engineering Analysis Time: 2 hour Date:27-11-2022 کورس اول تحليلات تعمیر ) 1st month exam / 1st semester (2022-2023)/11/27 Note: Answer all questions,all questions have same degree. Q1/: Find the following for three only. 1- 4s C-1 (+2-3)2 (219) 3.0 (6+1)) (+3+5) (82+28-3),2- ,3- 2-1 4- Q2/:Determine the Laplace transform of the function t sint. Q3/: Find the Laplace transform of 1, 0≤t<2, -2t+1, 2≤t<3, f(t) = 3t, t-1, 3≤t 5, t≥ 5 Q4: Find the Fourier series corresponding to the function 0 -5arrow_forward3. Construct a triangle in the Poincare plane with all sides equal to ln(2). (Hint: Use the fact that, the circle with center (0,a) and radius ln(r), r>1 in the Poincaré plane is equal to the point set { (x,y) : x^2+(y-1/2(r+1/r)a)^2=1/4(r-1/r)^2a^2 }arrow_forwardn. g. = neutral geometry <ABC = angle ABC \leq = less or equal than sqrt{x} = square root of x cLr = the line in the Poincaré plane defined by the equation (x-c)^2+y^2=r^2 1. Find the bisector of the angle <ABC in the Poincaré plane, where A=(0,5), B=(0,3) and C=(2,\sqrt{21})arrow_forward2. Let l=2L\sqrt{5} and P=(1,2) in the Poincaré plane. Find the uniqe line l' through P such that l' is orthogonal to l.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

