Fundamentals of Physics Extended
10th Edition
ISBN: 9781118230725
Author: David Halliday, Robert Resnick, Jearl Walker
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 32, Problem 24P
The magnitude of the electric field between the two circular parallel plates in Fig. 32-33 is E = (4.0 × 105) − (6.0 × 104t), with E in volts per meter and t in seconds. At t = 0,
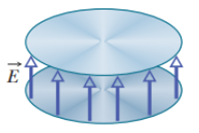
Figure 32-33 Problem 24.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A molecule of a substance has a permanent electric dipole moment of magnitude 10-29 C m. A mole of this substance is polarised (at low temperature) by applying a strong electrostatic field of magnitude 106 V m-1. The direction of the field is suddenly changed by an angle of 60º. Estimate the heat released by the substance in aligning its dipoles along the new direction of the field. For simplicity, assume 100% polarisation of the substance.
An electric field is found to be <3xyz, 2x2/z, x+y+z>. What is the x-component of the electric field vector at position (2, 6, 1)m?
Suppose a capacitor consists of two coaxial thin cylindrical conductors. The inner cylinder of radius ra has a charge of +Q, while the outer cylinder of radius rp has
charge -Q. The electric field E at a radial distance r from the central axis is given by the function:
E = aer/ao + B/r + bo
%|
where alpha (a), beta (B), ao and bo are constants. Find an expression for its capacitance.
First, let us derive the potential difference Vab between the two conductors. The potential difference is related to the electric field by:
Va
Edr=
Edr
Calculating the antiderivative or indefinite integral,
Vab = (-aaoe-r/ao + B
+ bo
By definition, the capacitance C is related to the charge and potential difference by:
C =
Evaluating with the upper and lower limits of integration for Vab, then simplifying:
C = Q/(
(e-"b/ao - era/ao) + B In(
) + bo (
))
Chapter 32 Solutions
Fundamentals of Physics Extended
Ch. 32 - Figure 32-19a shows a capacitor, with circular...Ch. 32 - Prob. 2QCh. 32 - Prob. 3QCh. 32 - Figure 32-22a shows a pair of opposite spin...Ch. 32 - An electron in an external magnetic field Bext has...Ch. 32 - Prob. 6QCh. 32 - Figure 32-23 shows a face-on view of one of the...Ch. 32 - Prob. 8QCh. 32 - Replace the current loops of Question 8 and Fig....Ch. 32 - Prob. 10Q
Ch. 32 - Figure 32-25 represents three rectangular samples...Ch. 32 - Prob. 12QCh. 32 - Prob. 1PCh. 32 - Prob. 2PCh. 32 - Prob. 3PCh. 32 - Prob. 4PCh. 32 - Prob. 5PCh. 32 - Prob. 6PCh. 32 - Prob. 7PCh. 32 - GO Nonuniform electric flux. Figure 32-30 shows a...Ch. 32 - Prob. 9PCh. 32 - Prob. 10PCh. 32 - Prob. 11PCh. 32 - Prob. 12PCh. 32 - Prob. 13PCh. 32 - Prob. 14PCh. 32 - Prob. 15PCh. 32 - Prob. 16PCh. 32 - Prob. 17PCh. 32 - Prob. 18PCh. 32 - Prob. 19PCh. 32 - Prob. 20PCh. 32 - Prob. 21PCh. 32 - Prob. 22PCh. 32 - Prob. 23PCh. 32 - The magnitude of the electric field between the...Ch. 32 - Prob. 25PCh. 32 - Prob. 26PCh. 32 - Prob. 27PCh. 32 - GO Figure 32-35a shows the current i that is...Ch. 32 - Prob. 29PCh. 32 - Assume the average value of the vertical component...Ch. 32 - In New Hampshire the average horizontal component...Ch. 32 - Figure 32-37a is a one-axis graph along which two...Ch. 32 - SSM WWWIf an electron in an atom has an orbital...Ch. 32 - Prob. 34PCh. 32 - What is the measured component of the orbital...Ch. 32 - Prob. 36PCh. 32 - Prob. 37PCh. 32 - Assume that an electron of mass m and charge...Ch. 32 - A sample of the paramagnetic salt to which the...Ch. 32 - A sample of the paramagnetic salt to which the...Ch. 32 - Prob. 41PCh. 32 - Prob. 42PCh. 32 - Prob. 43PCh. 32 - Figure 32-39 gives the magnetization curve for a...Ch. 32 - Prob. 45PCh. 32 - You place a magnetic compass on a horizontal...Ch. 32 - SSM ILW WWW The magnitude of the magnetic dipole...Ch. 32 - The magnitude of the dipole moment associated with...Ch. 32 - SSMThe exchange coupling mentioned in Module 32-8...Ch. 32 - Prob. 50PCh. 32 - Prob. 51PCh. 32 - Prob. 52PCh. 32 - Prob. 53PCh. 32 - Using the approximations given in Problem 61, find...Ch. 32 - Earth has a magnetic dipole moment of 8.0 1022...Ch. 32 - A charge q is distributed uniformly around a thin...Ch. 32 - A magnetic compass has its needle, of mass 0.050...Ch. 32 - Prob. 58PCh. 32 - Prob. 59PCh. 32 - Prob. 60PCh. 32 - SSMThe magnetic field of Earth can be approximated...Ch. 32 - Prob. 62PCh. 32 - Prob. 63PCh. 32 - A sample of the paramagnetic salt to which the...Ch. 32 - Prob. 65PCh. 32 - Prob. 66PCh. 32 - In Fig. 32-42, a parallel-plate capacitor is being...Ch. 32 - What is the measured component of the orbital...Ch. 32 - Prob. 69PCh. 32 - Prob. 70PCh. 32 - Prob. 71PCh. 32 - Prob. 72PCh. 32 - SSM If an electron in an atom has orbital angular...Ch. 32 - Prob. 74PCh. 32 - Prob. 75PCh. 32 - What are the measured components of the orbital...
Additional Science Textbook Solutions
Find more solutions based on key concepts
37. You're driving down the highway late one night at 20 m/s when a deer steps onto the road 35m in front of yo...
College Physics: A Strategic Approach (3rd Edition)
a. How can aspirin be synthesized from benzene? b. Ibuprofen is the active ingredient in pain relievers such as...
Organic Chemistry (8th Edition)
7. In an electricity experiment, a 1.0 g plastic ball is suspended on a 60-cm-long string and given an electr...
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Balance each chemical equation. a. MnO2(s)+HCl(aq)Cl2(g)+MnCl2(aq)+H2O(l) b. Co2(g)+CaSiO3(s)+H2O(l)SiO2(s)+Ca(...
Introductory Chemistry (6th Edition)
WRITE ABOUT A THEME: ENERGY In a short essay (about 100150 words), discuss how prokaryotes and other members of...
Campbell Biology (11th Edition)
1.1 Write a one-sentence definition for each of the following:
a. chemistry
b. chemical
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- An electric field is = sign(x)·(370 N/C), where sign(x) equals −1 if x < 0, 0 if x = 0, and +1 if x > 0. A cylinder of length L = 24 cm and radius R = 3.6 cm has its center at the origin and its axis along the x axis such that one end is at x= +12 cm and the other is at x = -12 cm. (a) What is the flux through each end? N · m2/C (+x end) N · m2/C (-x end)(b) What is the flux through the curved surface of the cylinder? N · m2/C(c) What is the net outward flux through the entire cylindrical surface? N · m2/C(d) What is the net charge inside the cylinder? Carrow_forwardProblem 3: The electric field in a certain region is given by the function E = Ak cos (kx) cos (by) i – Ab sin (kx) sin (by) where A = 18.06 N-m/C, k = 0.702 m ¹, and b = 1.29 m¹. The points in the figure use the values 1 1.5 m and u₁= 3.36 m. Part (a) What is the change in electric potential, in volts, from point (0, 0) to point (x₁, 0)? V(x₁,0) - V(0, 0) = Part (b) What is the change in potential, in volts, from point (x₁, 0) to point (x₁.y₁)? V(x1.₁) - V(x₁.0)=1 V V V (0,y₁) Part (c) What is the change in potential, in volts, from point (0, 0) to point (₁. ₁), along the path that passes through (x₁, 0)? V(x₁, y₁) - V(0, 0) = (0,0) (x₁₂V₁) (x₁,0)arrow_forwardSuppose a capacitor consists of two coaxial thin cylindrical conductors. The inner cylinder of radius ra has a charge of +Q, while the outer cylinder of radius rp has charge -Q. The electric field E at a radial distance r from the central axis is given by the function: E = aer/ao + B/r + bo %3D where alpha (a), beta (B), ao and bo are constants. Find an expression for its capacitance. First, let us derive the potential difference Vab between the two conductors. The potential difference is related to the electric field by: Vab = | S"Edr= - [ *Edr Calculating the antiderivative or indefinite integral, Vab = (-aage-r/ao + B + bo By definition, the capacitance C is related to the charge and potential difference by: C = Evaluating with the upper and lower limits of integration for Vab, then simplifying: C = Q/( (e-rb/ao - eralao) + B In( ) + bo ( ))arrow_forward
- The diagram below shows a section of a long thin-walled metal tube of radius R = 2.50 cm, with a chargo por unit longth of A = 2.00 x 10-8 C/m. (a). Determine the magnitude E of the electric field at radial distance: r= R/2.00 r= 2.00R (i) (ii) (b). Graph E versus r for the range r = 0 to 2.00R, indicating the maximum value of E as well.arrow_forwardER For the configuration shown in the figure below, suppose a = 5.00 cm, b = 20.0 cm, and c = 25.0 cm. Furthermore, suppose the electric field at a point 18.0 cm %3D from the center is measured to be 3.95 x 10 N/C radially inward and the electric field at a point 50.0 cm from the center is of magnitude 199 N/C and points radially outward. From this information, find the following. (Include the sign of the charge in your answer.) Insulator Conductor (a) the charge on the insulating sphere C (b) the net charge on the hollow conducting sphere (c) the charge on the outer surface of the hollow conducting sphere Carrow_forwardA solid metal cylinder of radius r = 1.9 cm is located coaxially inside a hollow metal cylinder of inner and outer radii rin = 13 cm and rout = 17 cm, respectively. Both cylinders have the same length L. Locations A and B are at distances da = 6.0 cm and dg = 24 cm, respectively. The electric fields at A and B are E = 1.25 x 10ªf N/C and Eg = -1.25 x 104f N/C, respectively. The diagram below shows the end view of the two cylinders. (a) What is the surface charge density on the outer surface of the inner cylinder? (b) What is the surface charge density on the inner surface of the outer cylinder? (c) What is the surface charge density on the outer surface of the outer cylinder?arrow_forward
- A square surface of side length L and parallel to the y-z plane is situated in an electric field given by E(x, y, z) = E[i+ a(yj + zk)/V(y + z) ]. The square's sides are parallel to the y- and z-axes and it is centered on the x-axis at position Py. Its normal vector points in the positive x-direction. a is a unitless constant. Refer to the figure. The x-axis points out of the screen. Pr Part (a) Integrate to find an expression for the total electric flux through the square surface in terms of defined quantities and enter the expression. Part (b) For L = 8.2 m, E, = 309.9 V/m, and a = 9.9, find the value of the flux, in units of volt•meter.arrow_forwardFor nos. 38-40, consider an insulating solid sphere, of radius a, with a uniform volume charge density p< 0, Is placed concentric with an insulating spherical shell, of Inner radius a and outer radius b, with a uniform charge density p> 0arrow_forwardThe square conducting sheet −2≤ x ≤2,−2≤ y ≤2,z=0 plane has a charge density12|y|mC/m2. Determine the total charge on the plate and the electric field intensity at(0,0,10)arrow_forward
- A uniform electric field of magnitude E = 22 N/C points along the x-axis. A circular loop of radius R = 13 cm is centered at the origin with the normal to the loop pointing θ = 55 degrees above the x-axis. part (a) Calculate the electric flux in units of N⋅m2/C that passes through the loop. Part (b) To what angle in degrees relative to the x-axis should the normal of the loop be rotated so that the flux through the loop becomes Φ' = 0.48 N⋅m2/C?arrow_forwardThe volumetric charge density of a cylinder of radius R is proportional to the distance to the center of the cylinder, that is, ρ = Ar when r≤R, with A being a constant. (a) Sketch the charge density for the region - 3R < r < 3R. What is the dimension of A?b) Calculate the electric field for a point outside the cylinder, r > Rc) Calculate the electric field for a point inside the cylinder, r<R.d) Sketch Exrarrow_forwardGiven Q1 = -5µC at origin and Q2 = 2 µC at x=10, where on the x-axis is the net electric field intensity equal to 0?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON
Electric Fields: Crash Course Physics #26; Author: CrashCourse;https://www.youtube.com/watch?v=mdulzEfQXDE;License: Standard YouTube License, CC-BY