
a.
Find the values
a.
Answer to Problem 16P
The values of
The values of
Explanation of Solution
Step-by-step procedure to verify
- Press STAT.
- Select Edit.
- Enter the values in L1.
- Press STAT and Choose CALC.
- Select 1-Var Stats.
- To select the variable L1, Press2-nd and then press 1.
- Press Enter.
The output obtained using the Ti83 calculator is as given below:
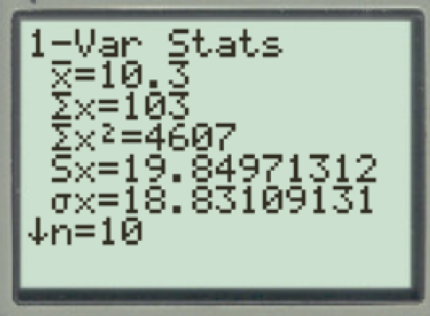
From the output, the values of
Step-by-step procedure to verify
- Press STAT.
- Select Edit.
- Enter the values in L2.
- Press STAT and Choose CALC.
- Select 1-Var Stats.
- To select the variable L2, Press2-nd and then press 2.
- Press Enter.
The output obtained using the Ti83 calculator is as given below:
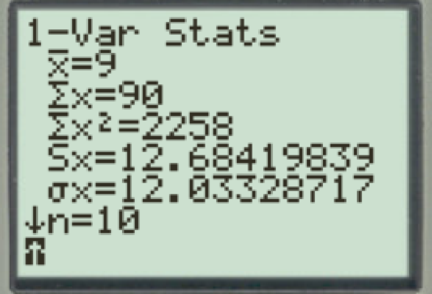
From the output, the values of
b.
Find the sample
b.
Answer to Problem 16P
The values of sample mean, variance, and standard deviation for x using the computation formula are10.3, 394.0, and 19.85, respectively.
The values of sample mean, variance, and standard deviation for y using the computation formula are9, 160.9, and 12.68, respectively.
Explanation of Solution
The sample variance using the computation formula is as follows:
Where,
The sample standard deviation using the computation formula is as follows:
Where,
The sample mean for x is obtained as given below:
Thus, the sample mean is 10.3.
The sample variance for x using the computation formula is obtained as given below:
Thus, the sample variance for x using the computation formula is 394.0.
The sample standard deviation for x using the computation formula is as obtained below:
Thus, the sample standard deviation for x using the computation formula is 19.85.
The sample mean for y is obtained as given below:
Thus, the sample mean is 9.
The sample variance for y using the computation formula is obtained as given below:
Thus, the sample variance for y using the computation formula is 160.9.
The sample standard deviation for y using the computation formula is obtained as given below:
Thus, the sample standard deviation for y using the computation formula is 12.68.
c.
Find the 75% Chebyshev interval around the mean for each fund.
Compare the two funds.
c.
Answer to Problem 16P
The 75% Chebyshev interval around the mean for the fund Vanguard Total Stock Index is–29.4 and 50.
The 75% Chebyshev interval around the mean for the fund Vanguard Balanced Index is –16.36 and 34.36.
Explanation of Solution
The 75% Chebyshev interval around the mean for the fund Vanguard Total Stock Index is obtained as given below:
Thus, the 75% Chebyshev interval around the mean for the fund Vanguard Total Stock Index is –29.4 and 50.
The 75% Chebyshev interval around the mean for the fund Vanguard Balanced Index is obtained as given below:
Thus, the 75% Chebyshev interval around the mean for the fund Vanguard Balanced Index is –16.36 and 34.36.
From the result, it is observed that the 75% returns lie in the 75% Chebyshev interval for both the funds.
d.
Find and compare the coefficient of variation for x and y.
d.
Answer to Problem 16P
The coefficient of variation for x is 192.7%.
The coefficient of variation for y is 140.9%.
Explanation of Solution
The formula for the coefficient of variation is as follows:
Where, s is the sample standard deviation and
The coefficient of variation for x is obtained as given below:
Thus, the coefficient of variation for x is 192.7%.
The coefficient of variation for y is obtained as given below:
Thus, the coefficient of variation for y is 140.9%.
From the results, the coefficient of variation for the fund Vanguard Balanced Index is less when compared to the coefficient of variation for the fund Vanguard Total Stock Index. Hence, the fund Vanguard Balanced Index has less risk per unit of return. Hence, the fund Vanguard Balanced Index appears to be better.
Want to see more full solutions like this?
Chapter 3 Solutions
WebAssign Printed Access Card for Brase/Brase's Understandable Statistics: Concepts and Methods, 12th Edition, Single-Term
- An Arts group holds a raffle. Each raffle ticket costs $2 and the raffle consists of 2500 tickets. The prize is a vacation worth $3,000. a. Determine your expected value if you buy one ticket. b. Determine your expected value if you buy five tickets. How much will the Arts group gain or lose if they sell all the tickets?arrow_forwardPlease show as much work as possible to clearly show the steps you used to find each solution. If you plan to use a calculator, please be sure to clearly indicate your strategy. Consider the following game. It costs $3 each time you roll a six-sided number cube. If you roll a 6 you win $15. If you roll any other number, you receive nothing. a) Find the expected value of the game. b) If you play this game many times, will you expect to gain or lose money?arrow_forward= 12:02 WeBWorK / 2024 Fall Rafeek MTH23 D02 / 9.2 Testing the Mean mu / 3 38 WEBWORK Previous Problem Problem List Next Problem 9.2 Testing the Mean mu: Problem 3 (1 point) Test the claim that the population of sophomore college students has a mean grade point average greater than 2.2. Sample statistics include n = 71, x = 2.44, and s = 0.9. Use a significance level of a = 0.01. The test statistic is The P-Value is between : The final conclusion is < P-value < A. There is sufficient evidence to support the claim that the mean grade point average is greater than 2.2. ○ B. There is not sufficient evidence to support the claim that the mean grade point average is greater than 2.2. Note: You can earn partial credit on this problem. Note: You are in the Reduced Scoring Period. All work counts for 50% of the original. Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. . Oli wwm01.bcc.cuny.eduarrow_forward
- There are four white, fourteen blue and five green marbles in a bag. A marble is selected from the bag without looking. Find the odds of the following: The odds against selecting a green marble. The odds in favour of not selecting a green marble The odds in favor of the marble selected being either a white or a blue marble. What is true about the above odds? Explainarrow_forwardPlease show as much work as possible to clearly show the steps you used to find each solution. If you plan to use a calculator, please be sure to clearly indicate your strategy. 1. The probability of a soccer game in a particular league going into overtime is 0.125. Find the following: a. The odds in favour of a game going into overtime. b. The odds in favour of a game not going into overtime. c. If the teams in the league play 100 games in a season, about how many games would you expect to go into overtime?arrow_forwardexplain the importance of the Hypothesis test in a business setting, and give an example of a situation where it is helpful in business decision making.arrow_forward
- A college wants to estimate what students typically spend on textbooks. A report fromthe college bookstore observes that textbooks range in price from $22 to $186. Toobtain a 95% confidence level for a confidence interval estimate to plus or minus $10,how many students should the college survey? (We may estimate the populationstandard deviation as (range) ÷ 4.)arrow_forwardIn a study of how students give directions, forty volunteers were given the task ofexplaining to another person how to reach a destination. Researchers measured thefollowing five aspects of the subjects’ direction-giving behavior:• whether a map was available or if directions were given from memory without a map,• the gender of the direction-giver,• the distances given as part of the directions,• the number of times directions such as “north” or “left” were used,• the frequency of errors in directions. Identify each of the variables in this study, and whether each is quantitative orqualitative. For each quantitative variable, state whether it is discrete or continuous. Was this an observational study or an experimental study? Explain your answer.arrow_forwardexplain the difference between the confident interval and the confident level. provide an example to show how to correctly interpret a confidence interval.arrow_forward
- Sketch to scale the orbit of Earth about the sun. Graph Icarus’ orbit on the same set of axesWhile the sun is the center of Earth’s orbit, it is a focus of Icarus’ orbit. There aretwo points of intersection on the graph. Based on the graph, what is the approximate distance between the two points of intersection (in AU)?arrow_forwardThe diameters of ball bearings are distributed normally. The mean diameter is 67 millimeters and the standard deviation is 3 millimeters. Find the probability that the diameter of a selected bearing is greater than 63 millimeters. Round to four decimal places.arrow_forwardSuppose you like to keep a jar of change on your desk. Currently, the jar contains the following: 22 Pennies 27 Dimes 9 Nickels 30 Quarters What is the probability that you reach into the jar and randomly grab a penny and then, without replacement, a dime? Express as a fraction or a decimal number rounded to four decimal places.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning





