Algebra 1, Homework Practice Workbook (MERRILL ALGEBRA 1)
Algebra 1, Homework Practice Workbook (MERRILL ALGEBRA 1)
2nd Edition
ISBN: 9780076602919
Author: McGraw-Hill Education
Publisher: McGraw-Hill Education
bartleby

Concept explainers

Maximization
Have you ever seen a bridge in the shape of a parabola? Where is its maximum on the bridge? The maximum of that bridge is the highest point on that bridge. The process of finding the maximum of the bridge here is called the maximization.
bartleby

Videos

Question
Book Icon
Chapter 3.1, Problem 60HP
To determine

To compare the graphs of the same equation with two different domains

Expert Solution & Answer
Check Mark

Explanation of Solution

Given:

The given equation is: y=2x+1

When domain is x∈{1,2,3,4}

Calculation:

The range is: y∈{3,5,7,9}

And hence the ordered pair will be: (1,3),(2,5),(3,7) and (4,9) and are plotted on the graph.

Graph:

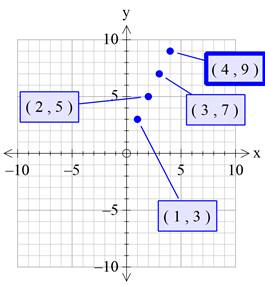
Algebra 1, Homework Practice Workbook (MERRILL ALGEBRA 1), Chapter 3.1, Problem 60HP , additional homework tip 1

Now when domain is : x∈R

Range will be : y∈R

Graph:

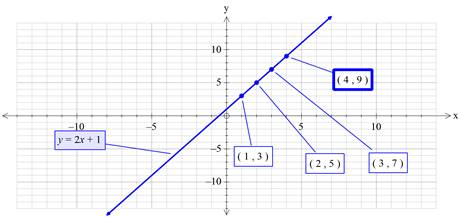
Algebra 1, Homework Practice Workbook (MERRILL ALGEBRA 1), Chapter 3.1, Problem 60HP , additional homework tip 2

Comparison:

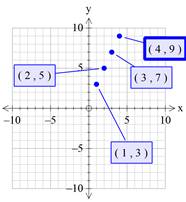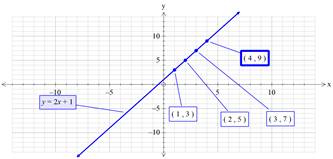
(1)Algebra 1, Homework Practice Workbook (MERRILL ALGEBRA 1), Chapter 3.1, Problem 60HP , additional homework tip 3(2)Algebra 1, Homework Practice Workbook (MERRILL ALGEBRA 1), Chapter 3.1, Problem 60HP , additional homework tip 4

When both the graphs are compared it can be concluded that both graph represent the same equation but there is difference of domain which creates the difference in Range. When the first graph is super imposed with the other graph, there is no difference can be seen as because the ordered pairs on the first graph will also be the ordered pair of second graph. In simple words it can be said that the ordered pair of first graph is the subset of the second graph.

Conclusion:

Graph (1) is the subset of graph (2).

Previous
Chapter 3.1, Problem 59HP
Next
Chapter 3.1, Problem 61HP

Chapter 3 Solutions

Algebra 1, Homework Practice Workbook (MERRILL ALGEBRA 1)

Ch. 3.1 - Prob. 1AGPCh. 3.1 - Prob. 1BGPCh. 3.1 - Prob. 2GPCh. 3.1 - Prob. 3GPCh. 3.1 - Prob. 4AGPCh. 3.1 - Prob. 4BGPCh. 3.1 - Prob. 5AGPCh. 3.1 - Prob. 5BGPCh. 3.1 - Prob. 5CGPCh. 3.1 - Prob. 1CYU
Ch. 3.1 - Prob. 2CYUCh. 3.1 - Prob. 3CYUCh. 3.1 - Prob. 4CYUCh. 3.1 - Prob. 5CYUCh. 3.1 - Prob. 6CYUCh. 3.1 - Prob. 7CYUCh. 3.1 - Prob. 8CYUCh. 3.1 - Prob. 9CYUCh. 3.1 - Prob. 10CYUCh. 3.1 - Prob. 11CYUCh. 3.1 - Prob. 12CYUCh. 3.1 - Prob. 13PPSCh. 3.1 - Prob. 14PPSCh. 3.1 - Prob. 15PPSCh. 3.1 - Prob. 16PPSCh. 3.1 - Prob. 17PPSCh. 3.1 - Prob. 18PPSCh. 3.1 - Prob. 19PPSCh. 3.1 - Prob. 20PPSCh. 3.1 - Prob. 21PPSCh. 3.1 - Prob. 22PPSCh. 3.1 - Prob. 23PPSCh. 3.1 - Prob. 24PPSCh. 3.1 - Prob. 25PPSCh. 3.1 - Prob. 26PPSCh. 3.1 - Prob. 27PPSCh. 3.1 - Prob. 28PPSCh. 3.1 - Prob. 29PPSCh. 3.1 - Prob. 30PPSCh. 3.1 - Prob. 31PPSCh. 3.1 - Prob. 32PPSCh. 3.1 - Prob. 33PPSCh. 3.1 - Prob. 34PPSCh. 3.1 - Prob. 35PPSCh. 3.1 - Prob. 36PPSCh. 3.1 - Prob. 37PPSCh. 3.1 - Prob. 38PPSCh. 3.1 - Prob. 39PPSCh. 3.1 - Prob. 40PPSCh. 3.1 - Prob. 41PPSCh. 3.1 - Prob. 42PPSCh. 3.1 - Prob. 43PPSCh. 3.1 - Prob. 44PPSCh. 3.1 - Prob. 45PPSCh. 3.1 - Prob. 46PPSCh. 3.1 - Prob. 47PPSCh. 3.1 - Prob. 48PPSCh. 3.1 - Prob. 49PPSCh. 3.1 - Prob. 50PPSCh. 3.1 - Prob. 51PPSCh. 3.1 - Prob. 52PPSCh. 3.1 - Prob. 53PPSCh. 3.1 - Prob. 54PPSCh. 3.1 - Prob. 55PPSCh. 3.1 - Prob. 56PPSCh. 3.1 - Prob. 57PPSCh. 3.1 - Prob. 58PPSCh. 3.1 - Prob. 59HPCh. 3.1 - Prob. 60HPCh. 3.1 - Prob. 61HPCh. 3.1 - Prob. 62HPCh. 3.1 - Prob. 63HPCh. 3.1 - Prob. 64HPCh. 3.1 - Prob. 65PFACh. 3.1 - Prob. 66PFACh. 3.1 - Prob. 67PFACh. 3.1 - Prob. 68PFACh. 3.2 - Prob. 1AGPCh. 3.2 - Prob. 1BGPCh. 3.2 - Prob. 2GPCh. 3.2 - Prob. 3GPCh. 3.2 - Prob. 1CYUCh. 3.2 - Prob. 2CYUCh. 3.2 - Prob. 3CYUCh. 3.2 - Prob. 4CYUCh. 3.2 - Prob. 5CYUCh. 3.2 - Prob. 6CYUCh. 3.2 - Prob. 7CYUCh. 3.2 - Prob. 8CYUCh. 3.2 - Prob. 9CYUCh. 3.2 - Prob. 10PPSCh. 3.2 - Prob. 11PPSCh. 3.2 - Prob. 12PPSCh. 3.2 - Prob. 13PPSCh. 3.2 - Prob. 14PPSCh. 3.2 - Prob. 15PPSCh. 3.2 - Prob. 16PPSCh. 3.2 - Prob. 17PPSCh. 3.2 - Prob. 18PPSCh. 3.2 - Prob. 19PPSCh. 3.2 - Prob. 20PPSCh. 3.2 - Prob. 21PPSCh. 3.2 - Prob. 22PPSCh. 3.2 - Prob. 23PPSCh. 3.2 - Prob. 24PPSCh. 3.2 - Prob. 25PPSCh. 3.2 - Prob. 26PPSCh. 3.2 - Prob. 27PPSCh. 3.2 - Prob. 28PPSCh. 3.2 - Prob. 29PPSCh. 3.2 - Prob. 30PPSCh. 3.2 - Prob. 31PPSCh. 3.2 - Prob. 32PPSCh. 3.2 - Prob. 33PPSCh. 3.2 - Prob. 34PPSCh. 3.2 - Prob. 35PPSCh. 3.2 - Prob. 36PPSCh. 3.2 - Prob. 37PPSCh. 3.2 - Prob. 38PPSCh. 3.2 - Prob. 39PPSCh. 3.2 - Prob. 40PPSCh. 3.2 - Prob. 41PPSCh. 3.2 - Prob. 42PPSCh. 3.2 - Prob. 43PPSCh. 3.2 - Prob. 44PPSCh. 3.2 - Prob. 45PPSCh. 3.2 - Prob. 46HPCh. 3.2 - Prob. 47HPCh. 3.2 - Prob. 48HPCh. 3.2 - Prob. 49HPCh. 3.2 - Prob. 50HPCh. 3.2 - Prob. 51PFACh. 3.2 - Prob. 52PFACh. 3.2 - Prob. 53PFACh. 3.2 - Prob. 54PFACh. 3.2 - Prob. 55PFACh. 3.2 - Prob. 56PFACh. 3.2 - Prob. 57PFACh. 3.2 - Prob. 58PFACh. 3.3 - Prob. 1AGPCh. 3.3 - Prob. 1BGPCh. 3.3 - Prob. 2GPCh. 3.3 - Prob. 3AGPCh. 3.3 - Prob. 3BGPCh. 3.3 - Prob. 4AGPCh. 3.3 - Prob. 4BGPCh. 3.3 - Prob. 4CGPCh. 3.3 - Prob. 5AGPCh. 3.3 - Prob. 5BGPCh. 3.3 - Prob. 6AGPCh. 3.3 - Prob. 6BGPCh. 3.3 - Prob. 1CYUCh. 3.3 - Prob. 2CYUCh. 3.3 - Prob. 3CYUCh. 3.3 - Prob. 4CYUCh. 3.3 - Prob. 5CYUCh. 3.3 - Prob. 6CYUCh. 3.3 - Prob. 7CYUCh. 3.3 - Prob. 8CYUCh. 3.3 - Prob. 9CYUCh. 3.3 - Prob. 10CYUCh. 3.3 - Prob. 11CYUCh. 3.3 - Prob. 12CYUCh. 3.3 - Prob. 13CYUCh. 3.3 - Prob. 14PPSCh. 3.3 - Prob. 15PPSCh. 3.3 - Prob. 16PPSCh. 3.3 - Prob. 17PPSCh. 3.3 - Prob. 18PPSCh. 3.3 - Prob. 19PPSCh. 3.3 - Prob. 20PPSCh. 3.3 - Prob. 21PPSCh. 3.3 - Prob. 22PPSCh. 3.3 - Prob. 23PPSCh. 3.3 - Prob. 24PPSCh. 3.3 - Prob. 25PPSCh. 3.3 - Prob. 26PPSCh. 3.3 - Prob. 27PPSCh. 3.3 - Prob. 28PPSCh. 3.3 - Prob. 29PPSCh. 3.3 - Prob. 30PPSCh. 3.3 - Prob. 31PPSCh. 3.3 - Prob. 32PPSCh. 3.3 - Prob. 33PPSCh. 3.3 - Prob. 34PPSCh. 3.3 - Prob. 35PPSCh. 3.3 - Prob. 36PPSCh. 3.3 - Prob. 37PPSCh. 3.3 - Prob. 38PPSCh. 3.3 - Prob. 39PPSCh. 3.3 - Prob. 40PPSCh. 3.3 - Prob. 41PPSCh. 3.3 - Prob. 42PPSCh. 3.3 - Prob. 43PPSCh. 3.3 - Prob. 44PPSCh. 3.3 - Prob. 45PPSCh. 3.3 - Prob. 46PPSCh. 3.3 - Prob. 47PPSCh. 3.3 - Prob. 48HPCh. 3.3 - Prob. 49HPCh. 3.3 - Prob. 50HPCh. 3.3 - Prob. 51HPCh. 3.3 - Prob. 52HPCh. 3.3 - Prob. 53PFACh. 3.3 - Prob. 54PFACh. 3.3 - Prob. 55PFACh. 3.3 - Prob. 56PFACh. 3.3 - Prob. 57PFACh. 3.3 - Prob. 58PFACh. 3.4 - Prob. 1AGPCh. 3.4 - Prob. 1BGPCh. 3.4 - Prob. 2AGPCh. 3.4 - Prob. 2BGPCh. 3.4 - Prob. 3AGPCh. 3.4 - Prob. 3BGPCh. 3.4 - Prob. 4GPCh. 3.4 - Prob. 5GPCh. 3.4 - Prob. 1CYUCh. 3.4 - Prob. 2CYUCh. 3.4 - Prob. 3CYUCh. 3.4 - Prob. 4CYUCh. 3.4 - Prob. 5CYUCh. 3.4 - Prob. 6CYUCh. 3.4 - Prob. 7CYUCh. 3.4 - Prob. 8CYUCh. 3.4 - Prob. 9CYUCh. 3.4 - Prob. 10CYUCh. 3.4 - Prob. 11CYUCh. 3.4 - Prob. 12CYUCh. 3.4 - Prob. 13CYUCh. 3.4 - Prob. 14CYUCh. 3.4 - Prob. 15CYUCh. 3.4 - Prob. 16CYUCh. 3.4 - Prob. 17PPSCh. 3.4 - Prob. 18PPSCh. 3.4 - Prob. 19PPSCh. 3.4 - Prob. 20PPSCh. 3.4 - Prob. 21PPSCh. 3.4 - Prob. 22PPSCh. 3.4 - Prob. 23PPSCh. 3.4 - Prob. 24PPSCh. 3.4 - Prob. 25PPSCh. 3.4 - Prob. 26PPSCh. 3.4 - Prob. 27PPSCh. 3.4 - Prob. 28PPSCh. 3.4 - Prob. 29PPSCh. 3.4 - Prob. 30PPSCh. 3.4 - Prob. 31PPSCh. 3.4 - Prob. 32PPSCh. 3.4 - Prob. 33PPSCh. 3.4 - Prob. 34PPSCh. 3.4 - Prob. 35PPSCh. 3.4 - Prob. 36PPSCh. 3.4 - Prob. 37PPSCh. 3.4 - Prob. 38PPSCh. 3.4 - Prob. 39PPSCh. 3.4 - Prob. 40PPSCh. 3.4 - Prob. 41PPSCh. 3.4 - Prob. 42PPSCh. 3.4 - Prob. 43PPSCh. 3.4 - Prob. 44PPSCh. 3.4 - Prob. 45PPSCh. 3.4 - Prob. 46PPSCh. 3.4 - Prob. 47PPSCh. 3.4 - Prob. 48PPSCh. 3.4 - Prob. 49PPSCh. 3.4 - Prob. 50PPSCh. 3.4 - Prob. 51PPSCh. 3.4 - Prob. 52PPSCh. 3.4 - Prob. 53PPSCh. 3.4 - Prob. 54PPSCh. 3.4 - Prob. 55PPSCh. 3.4 - Prob. 56PPSCh. 3.4 - Prob. 57PPSCh. 3.4 - Prob. 58PPSCh. 3.4 - Prob. 59PPSCh. 3.4 - Prob. 60PPSCh. 3.4 - Prob. 61PPSCh. 3.4 - Prob. 62HPCh. 3.4 - Prob. 63HPCh. 3.4 - Prob. 64HPCh. 3.4 - Prob. 65HPCh. 3.4 - Prob. 66HPCh. 3.4 - Prob. 67PFACh. 3.4 - Prob. 68PFACh. 3.4 - Prob. 69PFACh. 3.4 - Prob. 70PFACh. 3.4 - Prob. 71PFACh. 3.4 - Prob. 72PFACh. 3.4 - Prob. 73PFACh. 3.4 - Prob. 74PFACh. 3.5 - Prob. 1AGPCh. 3.5 - Prob. 1BGPCh. 3.5 - Prob. 2AGPCh. 3.5 - Prob. 2BGPCh. 3.5 - Prob. 3AGPCh. 3.5 - Prob. 3BGPCh. 3.5 - Prob. 4AGPCh. 3.5 - Prob. 4BGPCh. 3.5 - Prob. 5GPCh. 3.5 - Prob. 6GPCh. 3.5 - Prob. 1CYUCh. 3.5 - Prob. 2CYUCh. 3.5 - Prob. 3CYUCh. 3.5 - Prob. 4CYUCh. 3.5 - Prob. 5CYUCh. 3.5 - Prob. 6CYUCh. 3.5 - Prob. 7CYUCh. 3.5 - Prob. 8CYUCh. 3.5 - Prob. 9CYUCh. 3.5 - Prob. 10CYUCh. 3.5 - Prob. 11CYUCh. 3.5 - Prob. 12PPSCh. 3.5 - Prob. 13PPSCh. 3.5 - Prob. 14PPSCh. 3.5 - Prob. 15PPSCh. 3.5 - Prob. 16PPSCh. 3.5 - Prob. 17PPSCh. 3.5 - Prob. 18PPSCh. 3.5 - Prob. 19PPSCh. 3.5 - Prob. 20PPSCh. 3.5 - Prob. 21PPSCh. 3.5 - Prob. 22PPSCh. 3.5 - Prob. 23PPSCh. 3.5 - Prob. 24PPSCh. 3.5 - Prob. 25PPSCh. 3.5 - Prob. 26PPSCh. 3.5 - Prob. 27PPSCh. 3.5 - Prob. 28PPSCh. 3.5 - Prob. 29PPSCh. 3.5 - Prob. 30PPSCh. 3.5 - Prob. 31PPSCh. 3.5 - Prob. 32PPSCh. 3.5 - Prob. 33PPSCh. 3.5 - Prob. 34PPSCh. 3.5 - Prob. 35PPSCh. 3.5 - Prob. 36PPSCh. 3.5 - Prob. 37PPSCh. 3.5 - Prob. 38PPSCh. 3.5 - Prob. 39PPSCh. 3.5 - Prob. 40PPSCh. 3.5 - Prob. 41PPSCh. 3.5 - Prob. 42PPSCh. 3.5 - Prob. 43PPSCh. 3.5 - Prob. 44PPSCh. 3.5 - Prob. 45PPSCh. 3.5 - Prob. 46PPSCh. 3.5 - Prob. 47PPSCh. 3.5 - Prob. 48PPSCh. 3.5 - Prob. 49PPSCh. 3.5 - Prob. 50PPSCh. 3.5 - Prob. 51PPSCh. 3.5 - Prob. 52HPCh. 3.5 - Prob. 53HPCh. 3.5 - Prob. 54HPCh. 3.5 - Prob. 55HPCh. 3.5 - Prob. 56HPCh. 3.5 - Prob. 57PFACh. 3.5 - Prob. 58PFACh. 3.5 - Prob. 59PFACh. 3.5 - Prob. 60PFACh. 3.5 - Prob. 61PFACh. 3.5 - Prob. 62PFACh. 3.5 - Prob. 63PFACh. 3.5 - Prob. 64PFACh. 3.6 - Prob. 1AGPCh. 3.6 - Prob. 1BGPCh. 3.6 - Prob. 2GPCh. 3.6 - Prob. 3AGPCh. 3.6 - Prob. 3BGPCh. 3.6 - Prob. 3CGPCh. 3.6 - Prob. 3DGPCh. 3.6 - Prob. 4GPCh. 3.6 - Prob. 1CYUCh. 3.6 - Prob. 2CYUCh. 3.6 - Prob. 3CYUCh. 3.6 - Prob. 4CYUCh. 3.6 - Prob. 5CYUCh. 3.6 - Prob. 6CYUCh. 3.6 - Prob. 7CYUCh. 3.6 - Prob. 8PPSCh. 3.6 - Prob. 9PPSCh. 3.6 - Prob. 10PPSCh. 3.6 - Prob. 11PPSCh. 3.6 - Prob. 12PPSCh. 3.6 - Prob. 13PPSCh. 3.6 - Prob. 14PPSCh. 3.6 - Prob. 15PPSCh. 3.6 - Prob. 16PPSCh. 3.6 - Prob. 17PPSCh. 3.6 - Prob. 18PPSCh. 3.6 - Prob. 19PPSCh. 3.6 - Prob. 20PPSCh. 3.6 - Prob. 21PPSCh. 3.6 - Prob. 22PPSCh. 3.6 - Prob. 23PPSCh. 3.6 - Prob. 24PPSCh. 3.6 - Prob. 25PPSCh. 3.6 - Prob. 26PPSCh. 3.6 - Prob. 27PPSCh. 3.6 - Prob. 28PPSCh. 3.6 - Prob. 29PPSCh. 3.6 - Prob. 30PPSCh. 3.6 - Prob. 31PPSCh. 3.6 - Prob. 32HPCh. 3.6 - Prob. 33HPCh. 3.6 - Prob. 34HPCh. 3.6 - Prob. 35HPCh. 3.6 - Prob. 36HPCh. 3.6 - Prob. 37PFACh. 3.6 - Prob. 38PFACh. 3.6 - Prob. 39PFACh. 3.6 - Prob. 40PFACh. 3.6 - Prob. 41PFACh. 3.6 - Prob. 42PFACh. 3.6 - Prob. 43PFACh. 3.7 - Prob. 1GPCh. 3.7 - Prob. 2GPCh. 3.7 - Prob. 3GPCh. 3.7 - Prob. 4GPCh. 3.7 - Prob. 1CYUCh. 3.7 - Prob. 2CYUCh. 3.7 - Prob. 3CYUCh. 3.7 - Prob. 4CYUCh. 3.7 - Prob. 5CYUCh. 3.7 - Prob. 6CYUCh. 3.7 - Prob. 7CYUCh. 3.7 - Prob. 8PPSCh. 3.7 - Prob. 9PPSCh. 3.7 - Prob. 10PPSCh. 3.7 - Prob. 11PPSCh. 3.7 - Prob. 12PPSCh. 3.7 - Prob. 13PPSCh. 3.7 - Prob. 14PPSCh. 3.7 - Prob. 15PPSCh. 3.7 - Prob. 16PPSCh. 3.7 - Prob. 17PPSCh. 3.7 - Prob. 18PPSCh. 3.7 - Prob. 19PPSCh. 3.7 - Prob. 20PPSCh. 3.7 - Prob. 21PPSCh. 3.7 - Prob. 22PPSCh. 3.7 - Prob. 23PPSCh. 3.7 - Prob. 24PPSCh. 3.7 - Prob. 25PPSCh. 3.7 - Prob. 26PPSCh. 3.7 - Prob. 27PPSCh. 3.7 - Prob. 28PPSCh. 3.7 - Prob. 29PPSCh. 3.7 - Prob. 30PPSCh. 3.7 - Prob. 31PPSCh. 3.7 - Prob. 32PPSCh. 3.7 - Prob. 33PPSCh. 3.7 - Prob. 34PPSCh. 3.7 - Prob. 35PPSCh. 3.7 - Prob. 36PPSCh. 3.7 - Prob. 37HPCh. 3.7 - Prob. 38HPCh. 3.7 - Prob. 39HPCh. 3.7 - Prob. 40HPCh. 3.7 - Prob. 41PFACh. 3.7 - Prob. 42PFACh. 3.7 - Prob. 43PFACh. 3.7 - Prob. 44PFACh. 3.7 - Prob. 45PFACh. 3.8 - Prob. 1GPCh. 3.8 - Prob. 2GPCh. 3.8 - Prob. 3GPCh. 3.8 - Prob. 4GPCh. 3.8 - Prob. 5GPCh. 3.8 - Prob. 1CYUCh. 3.8 - Prob. 2CYUCh. 3.8 - Prob. 3CYUCh. 3.8 - Prob. 4CYUCh. 3.8 - Prob. 5CYUCh. 3.8 - Prob. 6CYUCh. 3.8 - Prob. 7CYUCh. 3.8 - Prob. 8CYUCh. 3.8 - Prob. 9CYUCh. 3.8 - Prob. 10CYUCh. 3.8 - Prob. 11CYUCh. 3.8 - Prob. 12CYUCh. 3.8 - Prob. 13CYUCh. 3.8 - Prob. 14PPSCh. 3.8 - Prob. 15PPSCh. 3.8 - Prob. 16PPSCh. 3.8 - Prob. 17PPSCh. 3.8 - Prob. 18PPSCh. 3.8 - Prob. 19PPSCh. 3.8 - Prob. 20PPSCh. 3.8 - Prob. 21PPSCh. 3.8 - Prob. 22PPSCh. 3.8 - Prob. 23PPSCh. 3.8 - Prob. 24PPSCh. 3.8 - Prob. 25PPSCh. 3.8 - Prob. 26PPSCh. 3.8 - Prob. 27PPSCh. 3.8 - Prob. 28PPSCh. 3.8 - Prob. 29PPSCh. 3.8 - Prob. 30PPSCh. 3.8 - Prob. 31PPSCh. 3.8 - Prob. 32PPSCh. 3.8 - Prob. 33PPSCh. 3.8 - Prob. 34PPSCh. 3.8 - Prob. 35PPSCh. 3.8 - Prob. 36PPSCh. 3.8 - Prob. 37PPSCh. 3.8 - Prob. 38PPSCh. 3.8 - Prob. 39PPSCh. 3.8 - Prob. 40PPSCh. 3.8 - Prob. 41PPSCh. 3.8 - Prob. 42PPSCh. 3.8 - Prob. 43PPSCh. 3.8 - Prob. 44PPSCh. 3.8 - Prob. 45PPSCh. 3.8 - Prob. 46PPSCh. 3.8 - Prob. 47PPSCh. 3.8 - Prob. 48PPSCh. 3.8 - Prob. 49PPSCh. 3.8 - Prob. 50PPSCh. 3.8 - Prob. 51PPSCh. 3.8 - Prob. 52PPSCh. 3.8 - Prob. 53PPSCh. 3.8 - Prob. 54HPCh. 3.8 - Prob. 55HPCh. 3.8 - Prob. 56HPCh. 3.8 - Prob. 57HPCh. 3.8 - Prob. 58HPCh. 3.8 - Prob. 59HPCh. 3.8 - Prob. 60PFACh. 3.8 - Prob. 61PFACh. 3.8 - Prob. 62PFACh. 3.8 - Prob. 63PFACh. 3.8 - Prob. 64PFACh. 3.8 - Prob. 65PFACh. 3.8 - Prob. 66PFACh. 3 - Prob. 1MCQCh. 3 - Prob. 2MCQCh. 3 - Prob. 3MCQCh. 3 - Prob. 4MCQCh. 3 - Prob. 5MCQCh. 3 - Prob. 6MCQCh. 3 - Prob. 7MCQCh. 3 - Prob. 8MCQCh. 3 - Prob. 9MCQCh. 3 - Prob. 10MCQCh. 3 - Prob. 11MCQCh. 3 - Prob. 12MCQCh. 3 - Prob. 13MCQCh. 3 - Prob. 14MCQCh. 3 - Prob. 15MCQCh. 3 - Prob. 16MCQCh. 3 - Prob. 17MCQCh. 3 - Prob. 18MCQCh. 3 - Prob. 19MCQCh. 3 - Prob. 20MCQCh. 3 - Prob. 21MCQCh. 3 - Prob. 22MCQCh. 3 - Prob. 23MCQCh. 3 - Prob. 24MCQCh. 3 - Prob. 25MCQCh. 3 - Prob. 26MCQCh. 3 - Prob. 1SGRCh. 3 - Prob. 2SGRCh. 3 - Prob. 3SGRCh. 3 - Prob. 4SGRCh. 3 - Prob. 5SGRCh. 3 - Prob. 6SGRCh. 3 - Prob. 7SGRCh. 3 - Prob. 8SGRCh. 3 - Prob. 9SGRCh. 3 - Prob. 10SGRCh. 3 - Prob. 11SGRCh. 3 - Prob. 12SGRCh. 3 - Prob. 13SGRCh. 3 - Prob. 14SGRCh. 3 - Prob. 15SGRCh. 3 - Prob. 16SGRCh. 3 - Prob. 17SGRCh. 3 - Prob. 18SGRCh. 3 - Prob. 19SGRCh. 3 - Prob. 20SGRCh. 3 - Prob. 21SGRCh. 3 - Prob. 22SGRCh. 3 - Prob. 23SGRCh. 3 - Prob. 24SGRCh. 3 - Prob. 25SGRCh. 3 - Prob. 26SGRCh. 3 - Prob. 27SGRCh. 3 - Prob. 28SGRCh. 3 - Prob. 29SGRCh. 3 - Prob. 30SGRCh. 3 - Prob. 31SGRCh. 3 - Prob. 32SGRCh. 3 - Prob. 33SGRCh. 3 - Prob. 34SGRCh. 3 - Prob. 35SGRCh. 3 - Prob. 36SGRCh. 3 - Prob. 37SGRCh. 3 - Prob. 38SGRCh. 3 - Prob. 39SGRCh. 3 - Prob. 40SGRCh. 3 - Prob. 41SGRCh. 3 - Prob. 42SGRCh. 3 - Prob. 43SGRCh. 3 - Prob. 44SGRCh. 3 - Prob. 45SGRCh. 3 - Prob. 46SGRCh. 3 - Prob. 47SGRCh. 3 - Prob. 48SGRCh. 3 - Prob. 49SGRCh. 3 - Prob. 50SGRCh. 3 - Prob. 51SGRCh. 3 - Prob. 52SGRCh. 3 - Prob. 53SGRCh. 3 - Prob. 54SGRCh. 3 - Prob. 55SGRCh. 3 - Prob. 56SGRCh. 3 - Prob. 57SGRCh. 3 - Prob. 58SGRCh. 3 - Prob. 59SGRCh. 3 - Prob. 60SGRCh. 3 - Prob. 61SGRCh. 3 - Prob. 62SGRCh. 3 - Prob. 63SGRCh. 3 - Prob. 64SGRCh. 3 - Prob. 65SGRCh. 3 - Prob. 66SGRCh. 3 - Prob. 67SGRCh. 3 - Prob. 68SGRCh. 3 - Prob. 69SGRCh. 3 - Prob. 70SGRCh. 3 - Prob. 71SGRCh. 3 - Prob. 72SGRCh. 3 - Prob. 73SGRCh. 3 - Prob. 74SGRCh. 3 - Prob. 75SGRCh. 3 - Prob. 76SGRCh. 3 - Prob. 77SGRCh. 3 - Prob. 78SGRCh. 3 - Prob. 1PTCh. 3 - Prob. 2PTCh. 3 - Prob. 3PTCh. 3 - Prob. 4PTCh. 3 - Prob. 5PTCh. 3 - Prob. 6PTCh. 3 - Prob. 7PTCh. 3 - Prob. 8PTCh. 3 - Prob. 9PTCh. 3 - Prob. 10PTCh. 3 - Prob. 11PTCh. 3 - Prob. 12PTCh. 3 - Prob. 13PTCh. 3 - Prob. 14PTCh. 3 - Prob. 15PTCh. 3 - Prob. 16PTCh. 3 - Prob. 17PTCh. 3 - Prob. 18PTCh. 3 - Prob. 19PTCh. 3 - Prob. 20PTCh. 3 - Prob. 21PTCh. 3 - Prob. 22PTCh. 3 - Prob. 23PTCh. 3 - Prob. 24PTCh. 3 - Prob. 25PTCh. 3 - Prob. 26PTCh. 3 - Prob. 27PTCh. 3 - Prob. 1CRCh. 3 - Prob. 2CRCh. 3 - Prob. 3CRCh. 3 - Prob. 4CRCh. 3 - Prob. 5CRCh. 3 - Prob. 6CRCh. 3 - Prob. 7CRCh. 3 - Prob. 8CRCh. 3 - Prob. 9CRCh. 3 - Prob. 10CRCh. 3 - Prob. 11CRCh. 3 - Prob. 12CRCh. 3 - Prob. 13CRCh. 3 - Prob. 14CR

Additional Math Textbook Solutions

Find more solutions based on key concepts
CHECK POINT 1 Find a counterexample to show that the statement The product of two two-digit numbers is a three-...

Thinking Mathematically (6th Edition)

Suppose you toss one coin three times in a row and get heads, tails, heads (HTH). If you are interested in the ...

Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)

Other techniques Evaluate the following limits, where a and b are fixed real numbers. 51. limh016+h4h

Calculus: Early Transcendentals (2nd Edition)

Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...

Algebra and Trigonometry (6th Edition)

A linear equation is solved by using the intersection of graphs method. Find the solution by interpreting the g...

College Algebra with Modeling & Visualization (5th Edition)

Which series in Exercises 53–76 converge, and which diverge? Give reasons for your answers. If a series converg...

University Calculus: Early Transcendentals (4th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Finding The Focus and Directrix of a Parabola - Conic Sections; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=KYgmOTLbuqE;License: Standard YouTube License, CC-BY