Chapter 3.1, Problem 43E

Solution

To graph: the given function and find the y -intercept and the horizontal asymptote.

  

y -intercept − $\left(0,4\right)$

Horizontal asymptotes are $y=16$ and $y=0$ .

Given information:

The given function is $f\left(x\right)=\frac{16}{1+3e^{-2x}}$ .

Definition Used:

Logistic Growth Function:

Let a , b , c , and k be positive constants, with $b<1$ . A logistic growth function in x is a function that can be written in the form

  $f\left(x\right)=\frac{c}{1+a\cdot b^x}\text{ or }f\left(x\right)=\frac{c}{1+a\cdot e^{-kx}}$

Where the constant c is the limit to growth.

Explanation:

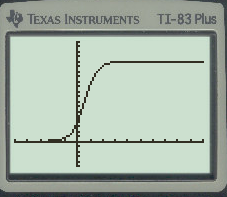
To graph the given function using Ti-83 calculator,

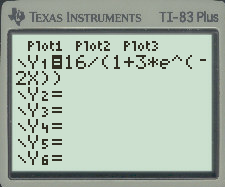
First pressand enter the function as shown:

  

Then press and set the window as shown:

  

Lastly press and this gives the required graph.

  

Now, to find the y -intercept substitute $x=0$ in the given function.

  $\begin{array}{c}f\left(0\right)=\frac{16}{1+3e^{-2\left(0\right)}}\\ =\frac{16}{1+3\left(1\right)}\\ =\frac{16}{4}\\ =4\end{array}$

So, y- intercept is $\left(0,4\right)$ .

By the above definition, the numerator of a logistic growth function is known as its limit to growth. Since, for any logistic growth function  f ( x ),

  $\underset{x\to \infty }{\lim }f\left(x\right)=c$

and thus  $y=c$  is a horizontal asymptote.

Here, the numerator of the given function is 16.

So, $y=16$  is a horizontal asymptote.

Also, every logistic growth function will approach zero as  x  tends to negative infinity, that is, for a logistic growth function  f ( x ),

  $\underset{x\to -\infty }{\lim }f\left(x\right)=0$

and thus  $y=0$ is a horizontal asymptote.