
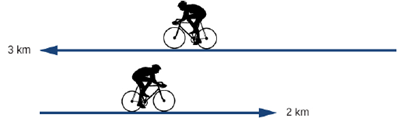
Check your Understanding A cyclist rides 3 km west and then tune around and tides 2 kin east. (a) What Is his displacement? (b) What is the distance traveled? (c) What is the magnitude of his displacement?
(a)
The displacement of the cyclist.
Answer to Problem 3.1CYU
The displacement of the cyclist is −1 km.
Explanation of Solution
Given:
Initially cyclist travel towards west and covers 3 km and then he turned towards east and travelled covering 2 km.
Formula used:
Displacement is defined as the change in position of an object. Numerically it is written as,
Δx=xf−xi
Where,
xf is the final position of the body.
xi is the initial position of the body.
Also, when there is a series of displacement, then total displacement is equal to the sum of individual displacements and it is written as,
ΔxT=∑Δxi
Calculation:
Consider that the cyclist starts from origin and east direction will be positive.
Initially cyclist moves 3 km towards west. The initial position of cyclist is 0 km and final position of cyclist is −3 km. So, the displacement for the first case will be,
Δx1=(−3)−0=−3 km
After travelling 3 km towards west, cyclist turns around and travels 2 km towards east. Now, the initial position of cyclist is −3 km and final position is −1 km. So, the displacement for the second case will be,
Δx1=(−1)−(−3)=−1+3=2 km
The total displacement will be,
ΔxT=Δx1+Δx2=−3+2=−1 km
Conclusion:
Therefore, the displacement of the cyclist is −1 km.
(b)
The distance travelled by the cyclist.
Answer to Problem 3.1CYU
The distance travelled by the cyclist is 5 km.
Explanation of Solution
Given:
Initially cyclist travel towards west and covers 3 km and then he turned towards east and travelled covering 2 km.
Formula used:
Distance travelled by an object is equal to the sum of magnitudes of individual displacements, ΔxTD=∑|Δxi|
Calculation:
The displacement for the first case is,
Δx1=−3 km
The displacement for the second case is,
Δx2=2 km
The total distance travelled is,
ΔxTD=|Δx1|+|Δx2|=|−3|+|2|=3+2=5 km
Conclusion:
Therefore, the distance travelled by the cyclist is 5 km.
(c)
The magnitude of the displacement.
Answer to Problem 3.1CYU
The magnitude of displacement of the cyclist is 1 km.
Explanation of Solution
Given:
Initially cyclist travel towards west and covers 3 km and then he turned towards east and travelled covering 2 km.
Formula used:
Displacement is defined as the change in position of an object. Numerically it is written as,
Δx=xf−xi
Where,
xf is the final position of the body.
xi is the initial position of the body.
Also, when there is a series of displacement, then total displacement is equal to the sum of individual displacements and it is written as,
ΔxT=∑Δxi
Calculation:
The displacement for the first case is,
Δx1=−3 km
The displacement for the second case is,
Δx2=2 km
The total displacement will be,
ΔxT=Δx1+Δx2=−3+2=−1 km
Magnitude of displacement is,
|ΔxT|=|−1|=1 km
Conclusion:
Therefore, the magnitude of displacement of the cyclist is 1 km.
Want to see more full solutions like this?
Chapter 3 Solutions
University Physics Volume 1
Additional Science Textbook Solutions
Concepts of Genetics (12th Edition)
College Physics: A Strategic Approach (3rd Edition)
Applications and Investigations in Earth Science (9th Edition)
Campbell Biology (11th Edition)
Cosmic Perspective Fundamentals
Introductory Chemistry (6th Edition)
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed. NOT AI PLSarrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardPlease don't use Chatgpt will upvote and give handwritten solutionarrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answerarrow_forward
- An electron and a proton are each accelerated through a potential difference of 21.0 million volts. Find the momentum (in MeV/c) and the kinetic energy (in MeV) of each, and compare with the results of using the classical formulas. Momentum (MeV/c) relativistic classical electron proton Kinetic Energy (MeV)arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 20.0 µF.) (a) Find the equivalent capacitance between points a and b. µF (b) Calculate the charge on each capacitor, taking ΔVab = 14.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forward11. At what point in SHM is the velocity maximum? Displacement maximum?arrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning





