
Concept explainers
a)
To discuss: Discount factor.
a)
Explanation of Solution
Computation of discount factors for each year is as follows:
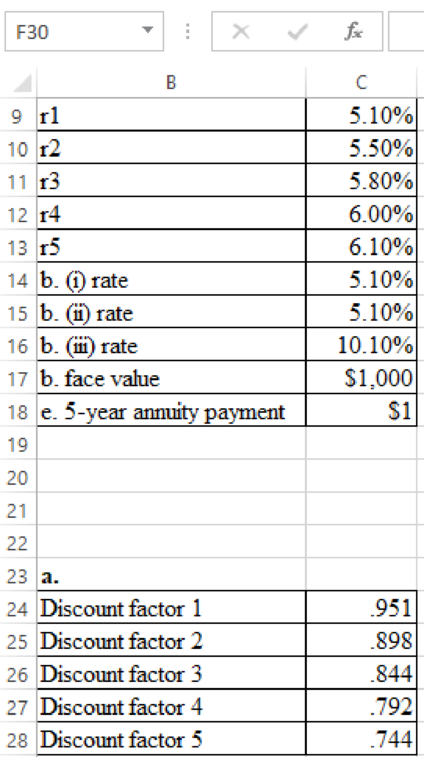
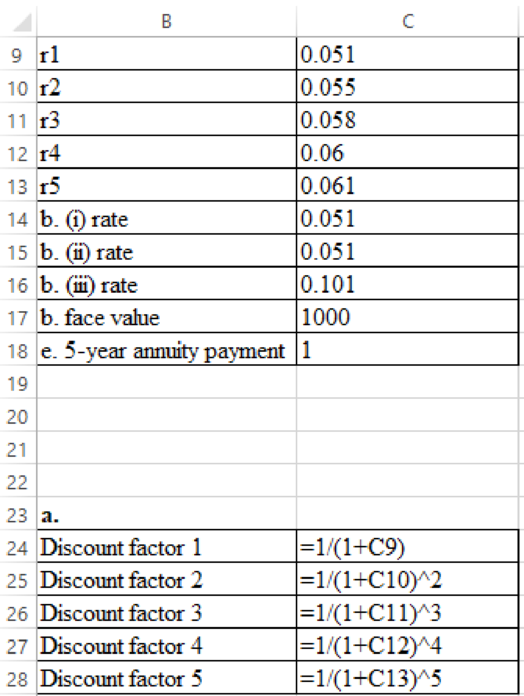
Formula to compute of discount factors for each year is as follows:
b)
To discuss: Present values.
b)
Explanation of Solution
Compute present values:
(i)
5%, 2-year bond
(ii)
5%, 5-year bond
(iii)
10%, 5-year bond
c)
To discuss: The reason why 10% bond is lower than 5% bond.
c)
Explanation of Solution
Fist compute the yield for these two bonds.
For the 5% bond:
The computation of r using the equation of
For the 10 % bond:
The yield of a bond is generally based on the current rate at the time of payment and the coupon payment. The 10% bond has a little better amount of its total payments, if the rate of interest is lesser than 5% of the bond Therefore, the yield of 10% bond is marginally lower.
d)
To discuss: The yield to maturity on 5 years zero coupon bond.
d)
Explanation of Solution
The computation of yield to maturity on 5 years zero coupon bond is as follows:
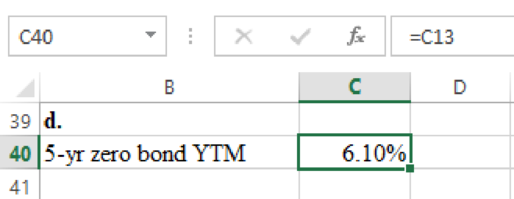
Hence the yield to maturity is 6.10%.
e)
To discuss: The yield to maturity on a 5-year
e)
Explanation of Solution
The calculation of yield to maturity on 5 years’

Formula to compute yield to maturity on 5 years annuity is as follows:
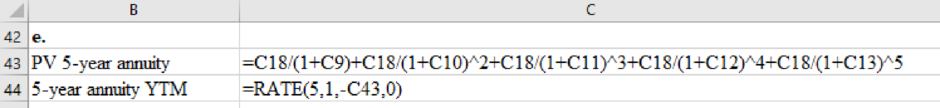
Hence the yield to maturity on 5years annuity is 5.845%.
f)
To discuss: Whether the 5-year bond lie between the yield of five years’
f)
Explanation of Solution
The yield on the five-year note lies amongst yield on a five-year
Want to see more full solutions like this?
Chapter 3 Solutions
Principles of Corporate Finance (Mcgraw-hill/Irwin Series in Finance, Insurance, and Real Estate)
- A firm needs to raise $950,000 but will incur flotation costs of 5%. How much will it pay in flotation costs? Multiple choice question. $55,500 $50,000 $47,500 $55,000arrow_forwardWhile determining the appropriate discount rate, if a firm uses a weighted average cost of capital that is unique to a particular project, it is using the Blank______. Multiple choice question. pure play approach economic value added method subjective approach security market line approacharrow_forwardWhen a company's interest payment Blank______, the company's tax bill Blank______. Multiple choice question. stays the same; increases decreases; decreases increases; decreases increases; increasesarrow_forward
- For the calculation of equity weights, the Blank______ value is used. Multiple choice question. historical average book marketarrow_forwardA firm needs to raise $950,000 but will incur flotation costs of 5%. How much will it pay in flotation costs? Multiple choice question. $50,000 $55,000 $55,500 $47,500arrow_forwardQuestion Mode Multiple Choice Question The issuance costs of new securities are referred to as Blank______ costs. Multiple choice question. exorbitant flotation sunk reparationarrow_forward
- What will happen to a company's tax bill if interest expense is deducted? Multiple choice question. The company's tax bill will increase. The company's tax bill will decrease. The company's tax bill will not be affected. The company's tax bill for the next year will be affected.arrow_forwardThe total market value of a firm is calculated as Blank______. Multiple choice question. the number of shares times the average price the number of shares times the future price the number of shares times the share price the number of shares times the issue pricearrow_forwardAccording the to the Blank______ approach for project evaluation, all proposed projects are placed into several risk categories. Multiple choice question. pure play divisional WACC subjectivearrow_forward
- To invest in a project, a company needs $50 million. Given its flotation costs of 7%, how much does the company need to raise? Multiple choice question. $53.76 million $46.50 million $50.00 million $53.50 millionarrow_forwardWhile determining the appropriate discount rate, if a firm uses a weighted average cost of capital that is unique to a particular project, it is using the Blank______. Multiple choice question. economic value added method pure play approach subjective approach security market line approacharrow_forwardWhat are flotation costs? Multiple choice question. They are the costs incurred to issue new securities in the market. They are the costs incurred to insure the payment due to bondholders. They are the costs incurred to meet day to day expenses. They are the costs incurred to keep a project in the business.arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





