
Concept explainers
For the waveforms in Fig. 26.32, determine whether the following will be present in the Fourier series representation:
a. dc term
b. cosine terms
c. sine terms
d. even-ordered harmonics
e. odd-ordered harmonics
(a)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is not present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 1.
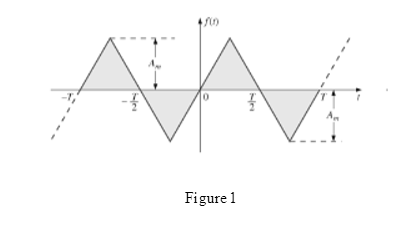
Case 1:
D.C. value is the average value of the waveform. And as the area above the horizontal axis and below the horizontal axis is equal, so the value of area and the average is zero for the waveform.
Therefore, D.C. term is not present in the waveform.
Case 2:
If waveform is symmetric about vertical axis, it has an even symmetry. And for an even symmetry, the wave Fourier series contains D.C. and cosine term.
As waveform is not symmetric about the vertical axis, it means cosine terms are not present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is symmetric about origin, it means sine terms are present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform does not contain cosine term, therefore, even ordered harmonics are not present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As the waveform contains sine term, therefore, odd ordered harmonics are present in the waveform.
Conclusion:
Thus, D.C. term is not present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
(b)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are not present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are not present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 2.
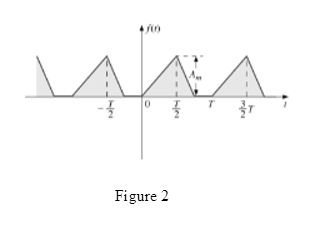
Case 1:
D.C. value is the average value of the waveform. And as area above the horizontal axis and below the horizontal axis is not equal so value of area and average is not zero for the waveform.
Therefore D.C. term is present in the waveform.
Case 2:
If waveform is symmetric about vertical axis it has even symmetry. And for even symmetry wave Fourier series contain D.C. and cosine term.
As waveform is not symmetric about vertical axis it means cosine terms are not present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is not symmetric about origin it means sine terms are not present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform does not contain cosine term therefore even ordered harmonics are not present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As waveform does not contains sine term therefore odd ordered harmonics are not present in the waveform.
Conclusion:
Thus, D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are not present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are not present in the waveform.
(c)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is present in the waveform, cosine terms are present in the waveform, sine terms are not present in the waveform, even ordered harmonics are present in the waveform and odd ordered harmonics are not present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 3.
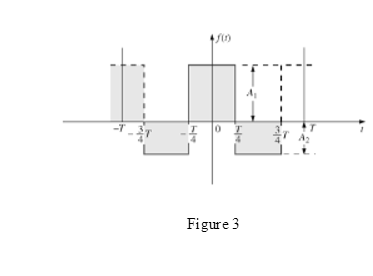
Case 1:
D.C. value is the average value of the waveform. And as area above the horizontal axis and below the horizontal axis is not equal so value of area and average is not zero for the waveform.
Therefore D.C. term is present in the waveform.
Case 2:
If waveform is symmetric about vertical axis it has even symmetry. And for even symmetry wave Fourier series contain D.C. and cosine term.
As waveform is symmetric about vertical axis it means cosine terms are present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is not symmetric about origin it means sine terms are not present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform contain cosine term therefore even ordered harmonics are present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As waveform does not contains sine term therefore odd ordered harmonics are not present in the waveform.
Conclusion:
Thus, D.C. term is present in the waveform, cosine terms are present in the waveform, sine terms are not present in the waveform, even ordered harmonics are present in the waveform and odd ordered harmonics are not present in the waveform.
(d)
Whether dc term, cosine terms, sine terms, even ordered harmonics and odd ordered harmonics will be present in the given Fourier Series representation or not.
Answer to Problem 1P
The D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
Explanation of Solution
Calculation:
The waveform for Fourier series representation is drawn as shown in Figure 4.
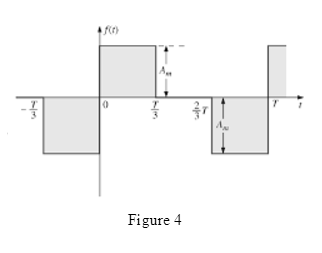
Case 1:
D.C. value is the average value of the waveform. And as area above the horizontal axis and below the horizontal axis is equal so value of area and average is zero for the waveform.
Therefore D.C. term is present in the waveform.
Case 2:
If waveform is symmetric about vertical axis it has even symmetry. And for even symmetry wave Fourier series contain D.C. and cosine term.
As waveform is not symmetric about vertical axis it means cosine terms are not present in the waveform.
Case 3:
If waveform is symmetric about origin it has odd symmetry. And for odd symmetry wave Fourier series contain D.C. and sine term.
As waveform is symmetric about origin it means sine terms are present in the waveform.
Case 4:
Cosine term is even function and sine terms are odd function.
As waveform does not contain cosine term therefore even ordered harmonics are not present in the waveform.
Case 5:
Cosine term is even function and sine terms are odd function.
As waveform contains sine term therefore odd ordered harmonics are present in the waveform.
Conclusion:
Thus, D.C. term is present in the waveform, cosine terms are not present in the waveform, sine terms are present in the waveform, even ordered harmonics are not present in the waveform and odd ordered harmonics are present in the waveform.
Want to see more full solutions like this?
Chapter 26 Solutions
Introductory Circuit Analysis (13th Edition)
- a) A periodic signal has a bandwidth of 60 Hz. Its middle frequency has a peak amplitude of 10 V. The highest frequency is 130 Hz. The two extreme frequencies have peak amplitudes of 1 V each. Draw the frequency spectrum of this signal showing all frequencies and amplitudes.arrow_forwardHello sir , I want the solution in detail , with an explanation of each step , please .. Thanks for the cooperationarrow_forwardDetermine the periodic time with given frequency of 2.5Hz A. 0.4s B. 0.04s C. 40us D. 100msarrow_forward
- Calculate bn for the following periodic waveform f(t) TO -2Tarrow_forwardAccording to Fourier analysis, which of the following can be said for the square wave? It consists of basic sine wave and double harmonics Olt consists of fundamental and sub-harmonic sine wave O It consists of basic sinūs wave and single harmonics Olt consists of basic sinūs wave and harmonicsarrow_forwardDetermine whether each of the following signal is periodic. If the signal is periodic, find its fundamental period.arrow_forward
- Ques. 5: Find the exponential Fourier series for a rectified sine wave.arrow_forwardDetermine whether or not each of the following signals is periodic. If a signalis periodic, determine its fundamental period.arrow_forwardDetermine whether or not each of the following signals is periodic. If a signalis periodic, determine its fundamental period.arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





