
Concept explainers
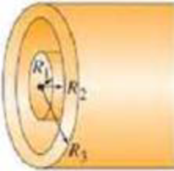
(II) A very long solid nonconducting cylinder of radius R1 is uniformly charged with a charge density ρE. It is surrounded by a concentric cylindrical tube of inner radius R2 and outer radius R3 as shown in Fig. 22–36, and it too carries a uniform charge density ρE. Determine the electric field as a function of the distance R from the center of the cylinders for (a) 0 < R < R1, (b) R1 < R < R2, (c) R2 < R < R3, and (d) R > R3. (e) If ρE = 15 μC/m3 and
FIGURE 22–36 Problem 38.
Want to see the full answer?
Check out a sample textbook solution
Chapter 22 Solutions
EBK PHYSICS FOR SCIENTISTS & ENGINEERS
Additional Science Textbook Solutions
Genetic Analysis: An Integrated Approach (3rd Edition)
Concepts of Genetics (12th Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Organic Chemistry (8th Edition)
Human Anatomy & Physiology (2nd Edition)
Campbell Biology (11th Edition)
- (iv)arrow_forward6 In Fig. 22-27, two identical circu- lar nonconducting rings are centered on the same line with their planes perpendicular to the line. Each ring has charge that is uniformly distrib- uted along its circumference. The rings each produce electric fields at points along the line. For three situations, the charges on rings A and B are, respectively, (1) qo and 9o, (2) -90 and -90, and (3) - and qo. Rank the situations according to the magnitude of the net electric field at (a) point P1 midway between the rings, (b) point P, at the center of ring B, and (c) point P3 to the right of ring B. greatest first. P, P3 Ring A Ring B Figure 22-27 Question 6.arrow_forward2) In Fig. 23-45, a small circular hole of radius R = 1.80 cm has een cut in the middle of an infinite, flat, nonconducting surface hat has uniform charge density o=4.50 pC/m². A z axis, with its rigin at the hole's center, is perpendicular to the surface. In unit- ector notation, what is the electric field at point P at z = 2.56 cm? Hint: See Eq. 22-26 and use superposition.) X X X X X X X X X X X X X X X X X XX X X X X 15 X XXX Z Figure 23-45 X X X X X X X X X X X X X X X X X X X X X X X X X X X Xarrow_forward
- The electric field everywhere on the surface of a charged sphere of radius 0.204 m has a magnitude of 510 N/C and points radially outward from th center of the sphere. (a) What is the net charge on the sphere? ]nc (b) What can you conclude about the nature and distribution of charge inside the sphere? Thie anewer hae not hean graded vetarrow_forward(II) The 1/r² form of Coulomb's law implies the following: (i) The electric field is zero at all points inside a uniformly charged shell. (ii) The electric field outside a uniformly charged sphere can be found by treating the charge as being concentrated at the center. Use these facts to show that within a uniformly charged sphere of radius R having a volume charge density p C/m³, the field strength increases linearly with the distance r from the center. That is, Ex r for r < R.arrow_forwardIgnore work donearrow_forward
- (II) The l/r2 form of Coulomb's law implies the following: (i) The electric field is zero at all points inside a uniformly charged shell. (ii) The electric field outside a uniformly charged sphere can be found by treating the charge as being concentrated at the center. Use these facts to show that within a uniformly charged sphere of radius R having a volume charge density p C/m3, the field strength increases linearly with the distance r from the center. That is, E ex r for r < R.arrow_forwardA very thin filament of uniform linear charge density "A" is located on the x-axis from x=0 to x=a. Prove that the components of the electric field at a point P on the y-axis, located at the distance "y" from the origin are:Ex = -k^(1/y-1/√/y² + a²) i, Ey = kha/y√/y² + a²)]arrow_forward(3) The purpose of this problem is to find the electric field of a ring of charge located in the x- z plane and has a diameter d. The ring has a total charge Q. To accomplish this, we will break the ring of charge into point charges. All answers should be given in terms given parameters and the coordinate 0. The field point, P, is located at (0, yo, 0). (a) What is the charge dq of the point charges? (b) What is the value of î for the point charges: (c) What are the bounds of integration to find the total electric field? (d) If instead of a full ring, we have half of a ring, which (if any) of your answers to parts (a) - (c) change? Which (if any) will stay the same?arrow_forward
- -24 Figure 23-40 shows a section of a long, thin-walled metal tube of radius R= 3.00 cm, with a charge per unit length of A = 2.00 x 10-8 C/m. What is the magnitude E of the electric field at radial distance (a) r= R2.00 and (b) r= 2.00R? (c) Graph E versus r for the range r = 0 to 2.00R.arrow_forward47. (III) A flat slab of nonconducting material has thickness 2d, which is small compared to its height and breadth. Define the x axis to be along the direction of the slab's thickness with the origin at the center of the slab (Fig. 22-41). If the slab carries a volume charge density PE(x) the region -d < x <0 and PE(x) = +po in the region 0 < xs +d, determine the electric field E as a function of x in the regions (a) outside the slab, = -Po in (b) 0 < x < +d, and (c) -d s x < 0. Let po be a positive constant. - +d FIGURE 22-41arrow_forwardPlease Asaparrow_forward
