
The circuit shown in Figure P21.47 is connected for 2.00 min. (a) Determine the current in each branch of the circuit. (b) Find the energy delivered by each battery. (c) Find the energy delivered to each resistor. (d) Identify the type of energy storage transformation that occurs in the operation of the circuit. (e) Find the total amount of energy transformed into internal energy in the resistors.
Figure P21.47 Problems 47 and 48.
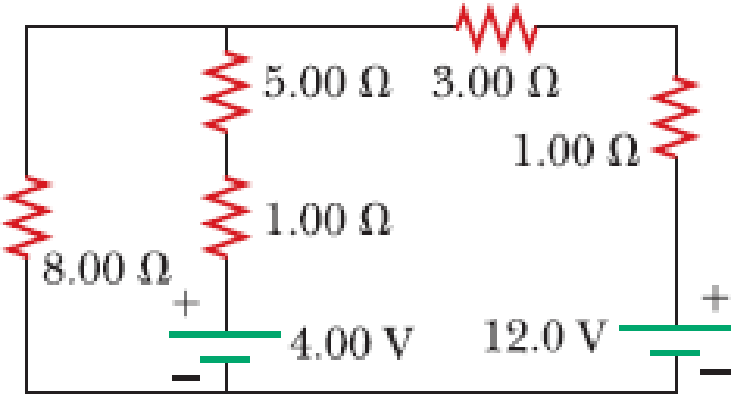
(a)
The current in each branch of the circuit.
Answer to Problem 47P
The current
Explanation of Solution
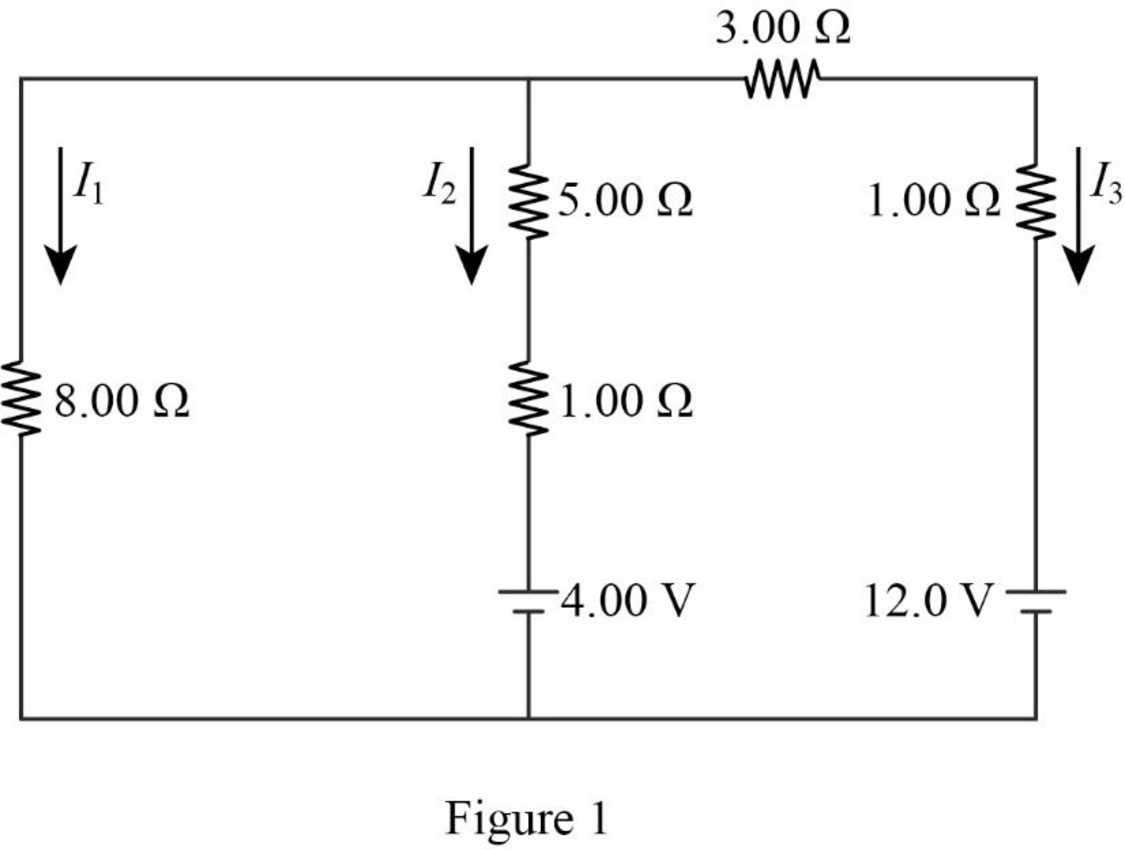
Write the expression for the Kirchhoff’s loop rule in second loop from the left of the figure
Here,
Write the expression for the Kirchhoff’s loop rule in first loop from the left of the figure
Write the expression for the Kirchhoff’s junction rule in the figure
Use equation (III) in (I) and solve the equation.
Use equation (II) to solve for
Use equation (IV) in (V) to solve for
Use equation (VI) to solve for
Use equation (VII) in (V) to solve for
Use equation (VIII) and (VII)in (III) to solve for
Conclusion:
Therefore, the current
(b)
The energy delivered to each battery.
Answer to Problem 47P
The energy delivered to
Explanation of Solution
Write the expression for the energy delivered to the battery.
Here,
Write the expression for the
Here,
Use equation (XI) in (X) to solve for
Conclusion:
Substitute
Substitute
Therefore, the energy delivered to
(c)
The energy delivered to each resistor.
Answer to Problem 47P
The energy delivered to
Explanation of Solution
Write the expression for the energy delivered to the resistor.
Here,
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Therefore, the energy delivered to
(d)
The type of energy transformation occurs in the operation of the circuit.
Answer to Problem 47P
The chemical energy is transformed to the internal energy in the resistors.
Explanation of Solution
The chemical energy in the
Conclusion:
Therefore, the chemical energy is transformed to the internal energy in the resistors.
(e)
The total amount of energy transformed into internal energy in the resistors.
Answer to Problem 47P
The total amount of energy transformed into internal energy in the resistors is
Explanation of Solution
Write the expression for the total amount of energy transformed into internal energy in the resistors.
Here,
Conclusion:
Substitute
Therefore, the total amount of energy transformed into internal energy in the resistors is
Want to see more full solutions like this?
Chapter 21 Solutions
Principles of Physics: A Calculus-Based Text
- No chatgpt pls will upvote Iarrow_forwardHow would partial obstruction of an air intake port of an air-entrainment mask effect FiO2 and flow?arrow_forward14 Z In figure, a closed surface with q=b= 0.4m/ C = 0.6m if the left edge of the closed surface at position X=a, if E is non-uniform and is given by € = (3 + 2x²) ŷ N/C, calculate the (3+2x²) net electric flux leaving the closed surface.arrow_forward
- No chatgpt pls will upvotearrow_forwardsuggest a reason ultrasound cleaning is better than cleaning by hand?arrow_forwardCheckpoint 4 The figure shows four orientations of an electric di- pole in an external electric field. Rank the orienta- tions according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the di- pole, greatest first. (1) (2) E (4)arrow_forward
- What is integrated science. What is fractional distillation What is simple distillationarrow_forward19:39 · C Chegg 1 69% ✓ The compound beam is fixed at Ę and supported by rollers at A and B. There are pins at C and D. Take F=1700 lb. (Figure 1) Figure 800 lb ||-5- F 600 lb بتا D E C BO 10 ft 5 ft 4 ft-—— 6 ft — 5 ft- Solved Part A The compound beam is fixed at E and... Hình ảnh có thể có bản quyền. Tìm hiểu thêm Problem A-12 % Chia sẻ kip 800 lb Truy cập ) D Lưu of C 600 lb |-sa+ 10ft 5ft 4ft6ft D E 5 ft- Trying Cheaa Những kết quả này có hữu ích không? There are pins at C and D To F-1200 Egue!) Chegg Solved The compound b... Có Không ☑ ||| Chegg 10 וחarrow_forwardNo chatgpt pls will upvotearrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





