
Concept explainers
Reports have found that many U.S. adults would rather live in a different type of community than the one in which they are living now. A national survey of 2,260 adults asked: “Where do you live now?” and “What do you consider to be the ideal community?” Response options were City (C), Suburb (S), Small Town (T), or Rural (R). A representative portion of this survey for a sample of 100 respondents is as follows:

- a. Provide a percent frequency distribution and a histogram for each question.
- b. Where are most adults living now?
- c. Where do most adults consider the ideal community to be?
- d. What changes in living areas would you expect to see if people moved from where they currently live to their ideal community?
a.
Create a percent frequency distribution and histogram for each question.
Answer to Problem 8P
The percent frequency distribution for each question is as follows:
Where do you live now?
| Living area | Frequency | Percent frequency |
| C | 32 | |
| R | 16 | |
| S | 26 | |
| T | 26 |
What do you consider to be the ideal community?
| Living area | Frequency | Percent frequency |
| C | 24 | |
| R | 21 | |
| S | 25 | |
| T | 30 |
The histogram for each question is as follows:
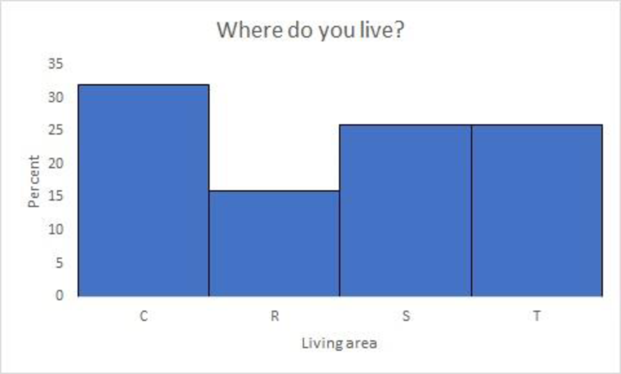
Where do you live now?
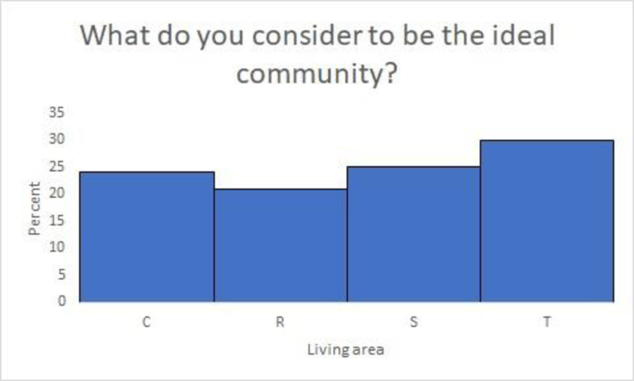
What do you consider to be the ideal community?
Explanation of Solution
Frequency distribution:
It is a table that summarizes the frequency of data values in each of several nonoverlapping bins.
Percent frequency distribution:
It is a table that summarizes the percentage of data values in each of the nonoverlapping bins.
Step-by-step procedure to obtain frequency data using EXCEL:
- Select A1:B101.
- Select Insert > PivotTable.
- Under Select a table or range, enter “$A$1:$A$101” in Table/Range.
- Click OK.
- Drag Where do you live now? to Rows.
- Drag Where do you live now? to ∑ Values.
- Click on Where do you live now? in ∑ Values.
- Select Value Field Settings.
- In Summarize value field by, choose Count and click OK.
- Now, click on Where do you live now? and Count of Where do you live now? in Drag fields between areas below and Remove Field.
- Drag What do you consider to be the ideal community? to Rows.
- Drag What do you consider to be the ideal community? to ∑ Values.
- Click on What do you consider to be the ideal community? in ∑ Values.
- Select Value Field Settings.
- In Summarize value field by, choose Count and click OK.
Outputs obtained is as follows:
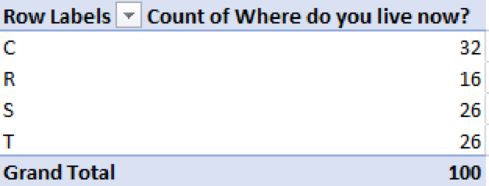
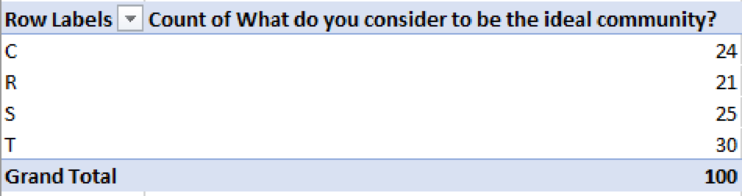
The percent frequency distribution for each question is computed as follows:
Where do you live now?
| Living area | Frequency | Percent frequency |
| C | 32 | |
| R | 16 | |
| S | 26 | |
| T | 26 | |
| Total | 100 | 100 |
What do you consider to be the ideal community?
| Living area | Frequency | Percent frequency |
| C | 24 | |
| R | 21 | |
| S | 25 | |
| T | 30 | |
| Total | 100 | 100 |
Step-by-step procedure to plot histogram using EXCEL:
- Select Insert.
- Choose Insert Column or Bar Chart under Charts.
- In Series Options, enter Gap Width as 0%.
Similarly, the histogram for the other question also obtained.
Thus, the percent frequency distribution and histogram are obtained.
b.
Find the community where most adults are living now.
Answer to Problem 8P
The most adults are living in City (C).
Explanation of Solution
From Part (a), it is clear that for the question “Where do you live now?”, the percent frequency for City (C) is 32, which is highest when compared to other community.
Therefore, the most adults are living in City (C).
c.
Find the community where most adults consider the ideal community to be.
Answer to Problem 8P
The community where most adults consider the ideal community is Small Town (T).
Explanation of Solution
From Part (a), it is clear that for the question “What do you consider to be the ideal community?”, the percent frequency for Small Town (T) is 30, which is highest when compared to other community.
Therefore, the most adults are living in Small Town (T).
d.
Explain the expected changes in living areas if people moved from where they currently live to their ideal community.
Explanation of Solution
The percent frequency distribution is obtained in Part (a). The difference between the percent frequencies for ideal community and currently living community is computed as follows:
| Living area | Living now | Ideal community | Difference |
| C | 32 | 24 | |
| R | 16 | 21 | |
| S | 26 | 25 | |
| T | 26 | 30 |
It is clear that there is no substantial change in Suburb living (S). However, the difference in percent between ideal community and currently living community is high for Small Town (T) and Rural (R). Hence, it would be expected that living in City (C) would decline, whereas, living in Small Towns (T) and Rural (R) would increase.
Want to see more full solutions like this?
Chapter 2 Solutions
Essentials of Business Analytics (MindTap Course List)
- You find out that the dietary scale you use each day is off by a factor of 2 ounces (over — at least that’s what you say!). The margin of error for your scale was plus or minus 0.5 ounces before you found this out. What’s the margin of error now?arrow_forwardSuppose that Sue and Bill each make a confidence interval out of the same data set, but Sue wants a confidence level of 80 percent compared to Bill’s 90 percent. How do their margins of error compare?arrow_forwardSuppose that you conduct a study twice, and the second time you use four times as many people as you did the first time. How does the change affect your margin of error? (Assume the other components remain constant.)arrow_forward
- Out of a sample of 200 babysitters, 70 percent are girls, and 30 percent are guys. What’s the margin of error for the percentage of female babysitters? Assume 95 percent confidence.What’s the margin of error for the percentage of male babysitters? Assume 95 percent confidence.arrow_forwardYou sample 100 fish in Pond A at the fish hatchery and find that they average 5.5 inches with a standard deviation of 1 inch. Your sample of 100 fish from Pond B has the same mean, but the standard deviation is 2 inches. How do the margins of error compare? (Assume the confidence levels are the same.)arrow_forwardA survey of 1,000 dental patients produces 450 people who floss their teeth adequately. What’s the margin of error for this result? Assume 90 percent confidence.arrow_forward
- The annual aggregate claim amount of an insurer follows a compound Poisson distribution with parameter 1,000. Individual claim amounts follow a Gamma distribution with shape parameter a = 750 and rate parameter λ = 0.25. 1. Generate 20,000 simulated aggregate claim values for the insurer, using a random number generator seed of 955.Display the first five simulated claim values in your answer script using the R function head(). 2. Plot the empirical density function of the simulated aggregate claim values from Question 1, setting the x-axis range from 2,600,000 to 3,300,000 and the y-axis range from 0 to 0.0000045. 3. Suggest a suitable distribution, including its parameters, that approximates the simulated aggregate claim values from Question 1. 4. Generate 20,000 values from your suggested distribution in Question 3 using a random number generator seed of 955. Use the R function head() to display the first five generated values in your answer script. 5. Plot the empirical density…arrow_forwardFind binomial probability if: x = 8, n = 10, p = 0.7 x= 3, n=5, p = 0.3 x = 4, n=7, p = 0.6 Quality Control: A factory produces light bulbs with a 2% defect rate. If a random sample of 20 bulbs is tested, what is the probability that exactly 2 bulbs are defective? (hint: p=2% or 0.02; x =2, n=20; use the same logic for the following problems) Marketing Campaign: A marketing company sends out 1,000 promotional emails. The probability of any email being opened is 0.15. What is the probability that exactly 150 emails will be opened? (hint: total emails or n=1000, x =150) Customer Satisfaction: A survey shows that 70% of customers are satisfied with a new product. Out of 10 randomly selected customers, what is the probability that at least 8 are satisfied? (hint: One of the keyword in this question is “at least 8”, it is not “exactly 8”, the correct formula for this should be = 1- (binom.dist(7, 10, 0.7, TRUE)). The part in the princess will give you the probability of seven and less than…arrow_forwardplease answer these questionsarrow_forward
- Selon une économiste d’une société financière, les dépenses moyennes pour « meubles et appareils de maison » ont été moins importantes pour les ménages de la région de Montréal, que celles de la région de Québec. Un échantillon aléatoire de 14 ménages pour la région de Montréal et de 16 ménages pour la région Québec est tiré et donne les données suivantes, en ce qui a trait aux dépenses pour ce secteur d’activité économique. On suppose que les données de chaque population sont distribuées selon une loi normale. Nous sommes intéressé à connaitre si les variances des populations sont égales.a) Faites le test d’hypothèse sur deux variances approprié au seuil de signification de 1 %. Inclure les informations suivantes : i. Hypothèse / Identification des populationsii. Valeur(s) critique(s) de Fiii. Règle de décisioniv. Valeur du rapport Fv. Décision et conclusion b) A partir des résultats obtenus en a), est-ce que l’hypothèse d’égalité des variances pour cette…arrow_forwardAccording to an economist from a financial company, the average expenditures on "furniture and household appliances" have been lower for households in the Montreal area than those in the Quebec region. A random sample of 14 households from the Montreal region and 16 households from the Quebec region was taken, providing the following data regarding expenditures in this economic sector. It is assumed that the data from each population are distributed normally. We are interested in knowing if the variances of the populations are equal. a) Perform the appropriate hypothesis test on two variances at a significance level of 1%. Include the following information: i. Hypothesis / Identification of populations ii. Critical F-value(s) iii. Decision rule iv. F-ratio value v. Decision and conclusion b) Based on the results obtained in a), is the hypothesis of equal variances for this socio-economic characteristic measured in these two populations upheld? c) Based on the results obtained in a),…arrow_forwardA major company in the Montreal area, offering a range of engineering services from project preparation to construction execution, and industrial project management, wants to ensure that the individuals who are responsible for project cost estimation and bid preparation demonstrate a certain uniformity in their estimates. The head of civil engineering and municipal services decided to structure an experimental plan to detect if there could be significant differences in project evaluation. Seven projects were selected, each of which had to be evaluated by each of the two estimators, with the order of the projects submitted being random. The obtained estimates are presented in the table below. a) Complete the table above by calculating: i. The differences (A-B) ii. The sum of the differences iii. The mean of the differences iv. The standard deviation of the differences b) What is the value of the t-statistic? c) What is the critical t-value for this test at a significance level of 1%?…arrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill


