
Concept explainers
(a)
Sketch for the condition
(a)
Answer to Problem 18PQ
The sketch for the condition
Explanation of Solution
Write an expression for the condition.
Here,
Here, y axis points upwards. The time starts at
Thus, the sketch for the condition
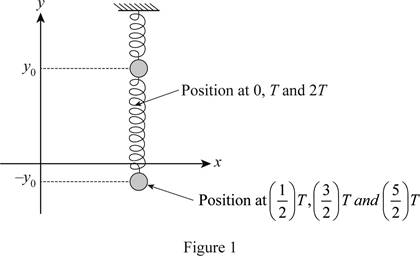
(b)
The position of the particle at
(b)
Answer to Problem 18PQ
The position of the particle at
Explanation of Solution
Write an expression for the condition.
Conclusion:
For
Substitute
For
Substitute
For
Substitute
For
Substitute
For
Substitute
For
Substitute
Thus, the particle can be seen at
Want to see more full solutions like this?
Chapter 2 Solutions
Webassign Printed Access Card For Katz's Physics For Scientists And Engineers: Foundations And Connections, 1st Edition, Single-term
- A mass on a spring undergoing simple harmonic motion completes 4.00 cycles in 14.0 s. a. What is the period of motion for this system? b. What is the frequency, in hertz, of this system? c. What is the angular frequency of this system?arrow_forwardA uniform annular ring of mass m and inner and outer radii a and b, respectively, is pivoted around an axis perpendicular to the plane of the ring at point P (Fig. P16.35). Determine its period of oscillation. FIGURE P16.35arrow_forwardThe equation of motion of a simple harmonic oscillator is given by x(t) = (18.0 cm) cos (10t) (16.0 cm) sin (10t), where t is in seconds. a. Find the amplitude. b. Determine the period. c. Determine the initial phase.arrow_forward
- (a) If frequency is not constant for some oscillation, can the oscillation be SHM? (b) Can you think of any examples of harmonic motion where the frequency may depend on the amplitude?arrow_forwardA simple pendulum of length L hangs from the ceiling of an elevator. a. While the elevator is moving up with constant acceleration a, is the period of the pendulum affected? If so, how? b. Now suppose we hang a particle of mass m on a spring of spring constant k and attach it to the ceiling of the same elevator. How does an upward acceleration a affect the period of this simple harmonic oscillator?arrow_forwardA particle of mass m moving in one dimension has potential energy U(x) = U0[2(x/a)2 (x/a)4], where U0 and a are positive constants. (a) Find the force F(x), which acts on the particle. (b) Sketch U(x). Find the positions of stable and unstable equilibrium. (c) What is the angular frequency of oscillations about the point of stable equilibrium? (d) What is the minimum speed the particle must have at the origin to escape to infinity? (e) At t = 0 the particle is at the origin and its velocity is positive and equal in magnitude to the escape speed of part (d). Find x(t) and sketch the result.arrow_forward
- A block of mass m = 5.94 kg is attached to a spring with spring constant k = 1592 N/m and rests on a frictionless surface. The block is pulled, stretching the spring a distance of 0.150 m, and is held still. The block is then released and moves in simple harmonic motion about the equilibrium position. a. What is the frequency of this oscillation? b. Where is the block located 3.24 s after it is released? c. What is the velocity of the mass at that time?arrow_forward(a) What is the effect on the period of a pendulum if you double its length? (b) What is the effect on the period of a pendulum if you decrease its length by 5.00%?arrow_forward(a) A pendulum that has a period of 3.00000 s and that is located where the acceleration due to gravity is 9.79 m/s2 is moved to a location where the acceleration due to gravity is 9.82 m/s2. What is its new period? (b) Explain why so many digits are needed in the value for the period, based on the relation between the period and the acceleration due to gravity.arrow_forward
- A Two particles A and B move at a constant speed in circular paths at the same angular speed . Particle As circle has a radius that is twice the length of particle Bs circle. What is the ratio TA/TB of their periods?arrow_forwardThe equations listed in Table 2.2 give position as a function of time, velocity as a function of time, and velocity as a function of position for an object moving in a straight line with constant acceleration. The quantity vxi appears in every equation. (a) Do any of these equations apply to an object moving in a straight line with simple harmonic motion? (b) Using a similar format, make a table of equations describing simple harmonic motion. Include equations giving acceleration as a function of time and acceleration as a function of position. State the equations in such a form that they apply equally to a blockspring system, to a pendulum, and to other vibrating systems. (c) What quantity appears in every equation?arrow_forwardYour grandfather clock's pendulum has a length of 0.9930 m. a. If the clock runs slow and loses 23 s per day, how should you adjust the length of the pendulum? Note: due to the precise nature of this problem you must treat the constant g as unknown (that is, do not assume it is equal to exactly 9.80 m/s2). Express your answer to two significant figures and include the appropriate units. Enter positive value in case of increasing length of the pendulum and negative value in case of decreasing length of the pendulum.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





