Chapter 1.9, Problem 73PS

Solution

To Find: The ages at a larvae's length tends to be greater than 10 millimetres. And state the given domain which affects the solution.

The ages at larvae's length tends to be greater than 10 millimetres is between $37$ and $40$ days after hatching.

Given information:

Given the inequality is $L\left(x\right)=0.00170x^2+0.145x+2.35,0\le x\le 40$

  $x=$ (Age in days) of the larvae.

Calculation:

Given that the larvae's length is greater than 10 millimetres.

Thus, $L\left(x\right)>10$

Substitute $0.00170x^2+0.145x+2.35$ for $L\left(x\right)$ :

  $0.00170x^2+0.145x+2.35>10$

Subtract $10$ from each side:

  $\begin{array}{l}0.00170x^2+0.145x+2.35-10>10-10\\ 0.00170x^2+0.145x-7.65>0\end{array}$

In order to solve the inequality, replace the inequality sign with $=$ sign.

  $0.00170x^2+0.145x-7.65=0$

To find the solutions of a quadratic equation of the form using factoring:

  $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$ , where $a,b,c$ are real numbers and $a\ne 0$ .

Substitute the values of $a=0.00170$ , $b=0.145$ and $c=-7.65$ in the above equation:

  $x=\frac{-0.145\pm \sqrt{{\left(0.145\right)}^2-4\left(0.00170\right)\left(-7.65\right)}}{2\left(0.00170\right)}$

Evaluate the square root and simplify.

  $x\approx \frac{-0.145\pm 0.270}{2(0.00170)}$

Simplify the above equation:

  $\begin{array}{l}x=\frac{-0.145+0.270}{2(0.00170)}\\ x\approx 36.84\end{array}$

Or

  $\begin{array}{l}x=\frac{-0.145-0.270}{2(0.00170)}\\ x\approx -122.13\end{array}$

Due to the fact that $x$ represents the larvae's age in days, the negative value of $x$ should be discarded. This means that $36.84$ is the critical $x$ value.

Create a number line. Using open dots, plot the critical $x$ -value $36.84$ , as it does not

satisfy the inequality.

  

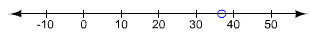
A critical $x-$ value divides the number line into two intervals. Find whether the inequality is satisfied by an $x-$ value in each interval.

$x$	$0.00170x^2+0.145x+2.35>10$
35	$9.507$
37	$10.04\ge 10$

There is a restriction that the number of days must be less than or equal to $40$ . Thus, $37<40$ .

It is therefore common for larvae to reach a length of more than 10 milli meters between $37$ and $40$ days after hatching.