
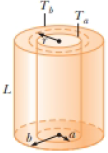
(a) The inside of a hollow cylinder is maintained at a temperature Ta, and the outside is at a lower temperature, Tb (Fig. P19.45). The wall of the cylinder has a thermal conductivity k. Ignoring end effects, show that the rate of energy
Suggestions: The temperature gradient is dT/dr. A radial energy current passes through a concentric cylinder of area 2πrL. (b) The passenger section of a jet airliner is in the shape of a cylindrical tube with a length of 35.0 m and an inner radius of 2.50 m. Its walls are lined with an insulating material 6.00 cm in thickness and having a thermal conductivity of 4.00 × 10−5 cal/s · cm · °C. A heater must maintain the interior temperature at 25.0°C while the outside temperature is −35.0°C. What power must be supplied to the heater?
Figure P19.45
Trending nowThis is a popular solution!

Chapter 19 Solutions
Physics for Scientists and Engineers
- No chatgpt pls will upvotearrow_forwarda cubic foot of argon at 20 degrees celsius is isentropically compressed from 1 atm to 425 KPa. What is the new temperature and density?arrow_forwardCalculate the variance of the calculated accelerations. The free fall height was 1753 mm. The measured release and catch times were: 222.22 800.00 61.11 641.67 0.00 588.89 11.11 588.89 8.33 588.89 11.11 588.89 5.56 586.11 2.78 583.33 Give in the answer window the calculated repeated experiment variance in m/s2.arrow_forward
- How can i solve this if n1 (refractive index of gas) and n2 (refractive index of plastic) is not known. And the brewsters angle isn't knownarrow_forward2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward2-3. Consider the situation of the reflection of a pulse at the interface of two string described in the previous problem. In addition to the net disturbances being equal at the junction, the slope of the net disturbances must also be equal at the junction at all times. Given that p1 = 4.0 g/m, H2 = 9.0 g/m and Aj = 0.50 cm find 2. A, (Answer: -0.10 cm) and 3. Ay. (Answer: 0.40 cm)please I need to show all work step by step problems 2 and 3arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





