
To calculate: The lengths of the medians of the triangle with the vertices
Answer to Problem 44E
The lengths of the medians of the triangle with vertices
Explanation of Solution
Given information:
The three vertices of the triangle
Formula used:
Median of a triangle is defined as the line segment joining two points from a vertex to the midpoint of the opposite side.
Mid-point formula between two points
Distance formula between two points
Calculation:
Consider the provided vertices of the triangle
Recall the mid-point formula between two points
Let D, E and F be the mid-points of line segments AB, BC and CA respectively.
So, mid-point of line segment
Now, mid-point of line segment
Mid-point of line segment
By plotting all the points on the coordinate plane, we get the following figure,
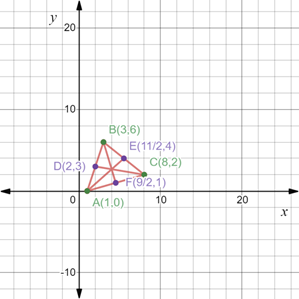
In the above figure, AE, BF and CD represents the three medians of the triangle ABC.
Recall the distance formula between two points
So, length of median AE is calculated as,
Length of median BF is calculated as,
Now, the length of median CD is calculated as,
Thus, the lengths of the medians of the triangle with vertices
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
- Only 100% sure experts solve it correct complete solutions okarrow_forwardrmine the immediate settlement for points A and B shown in figure below knowing that Aq,-200kN/m², E-20000kN/m², u=0.5, Depth of foundation (DF-0), thickness of layer below footing (H)=20m. 4m B 2m 2m A 2m + 2m 4marrow_forwardsy = f(x) + + + + + + + + + X 3 4 5 7 8 9 The function of shown in the figure is continuous on the closed interval [0, 9] and differentiable on the open interval (0, 9). Which of the following points satisfies conclusions of both the Intermediate Value Theorem and the Mean Value Theorem for f on the closed interval [0, 9] ? (A A B B C Darrow_forward
- = Q6 What will be the allowable bearing capacity of sand having p = 37° and ydry 19 kN/m³ for (i) 1.5 m strip foundation (ii) 1.5 m x 1.5 m square footing and (iii)1.5m x 2m rectangular footing. The footings are placed at a depth of 1.5 m below ground level. Assume F, = 2.5. Use Terzaghi's equations. 0 Ne Na Ny 35 57.8 41.4 42.4 40 95.7 81.3 100.4arrow_forwardQ1 The SPT records versus depth are given in table below. Find qan for the raft 12% foundation with BxB-10x10m and depth of raft D-2m, the allowable settlement is 50mm. Elevation, m 0.5 2 2 6.5 9.5 13 18 25 No.of blows, N 11 15 29 32 30 44 0 estigate shear 12%arrow_forwardQ2 A/ State the main field tests which may be carried out to investigate shear strength of a soil layer? B/ What are the main factors that affecting the spacing and number of boreholes for a given project? C/ Illustrate the causes of disturbance of Shelby tubes samples.arrow_forward
- Trolley of the overhead crane moves along the bridge rail. The trolley position is measured from the center of the bridge rail (x = 0) is given by x(t) = 0.5t^3-6t^2+19.5t-14 : 0 <= t <= 3 min. The trolley moves from point A to B in the forward direction, B to C in the reverse direction and C to D again in the forward direction. CONTROL PANEL END TRUCK- RUNWAY BEAM- BRIDGE RAIL HOIST -TROLLEY TROLLEY BUMPER TROLLEY DRIVE LPENDANT TRACK -TROLLEY CONDUCTOR TRACK WIRE ROPE -HOOK BLOCK -BRIDGE DRIVE -END TRUCK BUMPER -RUNWAY RAIL TROLLEY END STOP -CONDUCTOR BAR PENDANT FESTOONING TROLLEY FESTOONING PENDANT CABLE PENDANT x(t)=0.5t^3-6t^2+19.5t-14 v(t)=1.5t^2-12t+19.5 a(t)=(dv(t))/dt=3t-12 Fig. T2.2: The overhead crane Total masses of the trolley, hook block, and the load attached to the hook block are 110 kg, 20 kg, and 150 kg. Damping coefficient, D, is 40 kg/s. What is the total amount of energy required from the trolley motor to move the system [Hint: Use Newton's 2nd law to obtain the…arrow_forwardCONTROL PANEL- BRIDGE RAIL HOIST -TROLLEY TROLLEY BUMPER -BRIDGE DRIVE END TRUCK- RUNWAY BEAM- END TRUCK BUMPER -RUNWAY RAIL TROLLEY DRIVE TROLLEY END STOP -CONDUCTOR BAR LPENDANT TRACK TROLLEY CONDUCTOR TRACK -WIRE ROPE PENDANT FESTOONING TROLLEY FESTOONING -PENDANT CABLE -HOOK BLOCK PENDANTarrow_forwardchool Which of the following functions describes the graph of g(x)--2√9-x²+37 9 8 7 6 4 2 -10-9-8-7-6-5-4-3-2-1 1 -1 -2 -4 -6 10 9 8 B 5 4 3 3 6 -10-9-8-7-6-5-4-3-2-1 2 3 4 6 1 -2 4 -5 -6 -8 -9 -10 10 -10-9-8-7-6-5-4-3-2-1 9 8 Lessons Assessments 6 5 4 + 2 1 1 2 3 4 5 6 8 -1 2 4 -5 -B 8 10 10 9 8 7 6 5 4 3 2 1 -10-9-8-7-6-5-4-3-2-1 1 2 3 4 5 6 B 9 10 -1 -2 -3 -5arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





