Physics for Scientists and Engineers
10th Edition
ISBN: 9781337553278
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 17, Problem 22P
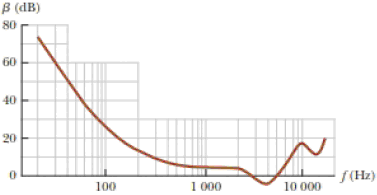
Ever since seeing Figure 16.22 in the previous chapter, you have been fascinated with the hearing response in humans. You have set up an apparatus that allows you to determine your own threshold of hearing as a function of frequency. After performing the experiment and recording the results, you graph the results, which look like Figure P17.22. You are intrigued by the two dips in the curve at the right-hand side of the graph. You measure carefully and find that the minimum values of these dips occur at 3 800 Hz and 11 500 Hz. Performing some online research, you discover that the outer canal of the human ear can be modeled as an air column open at the outer end and closed at the inner end by the eardrum. You use this information to determine the length of the outer canal in your car.
Figure P17.22
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
No chatgpt pls will upvote
No chatgpt pls will upvote
air is pushed steadily though a forced air pipe at a steady speed of 4.0 m/s. the pipe measures 56 cm by 22 cm. how fast will air move though a narrower portion of the pipe that is also rectangular and measures 32 cm by 22 cm
Chapter 17 Solutions
Physics for Scientists and Engineers
Ch. 17.1 - Prob. 17.1QQCh. 17.2 - Consider the waves in Figure 17.8 to be waves on a...Ch. 17.4 - When a standing wave is set up on a string fixed...Ch. 17.6 - Prob. 17.4QQCh. 17.6 - Balboa Park in San Diego has an outdoor organ....Ch. 17 - Two waves on one string are described by the wave...Ch. 17 - Two pulses of different amplitudes approach each...Ch. 17 - Two wave pulses A and B are moving in opposite...Ch. 17 - Why is the following situation impossible? Two...Ch. 17 - Two pulses traveling on the same string are...
Ch. 17 - Two identical loudspeakers 10.0 m apart are driven...Ch. 17 - Two sinusoidal waves on a string are defined by...Ch. 17 - Verify by direct substitution that the wave...Ch. 17 - Prob. 9PCh. 17 - A standing wave is described by the wave function...Ch. 17 - Prob. 11PCh. 17 - A taut string has a length of 2.60 m and is fixed...Ch. 17 - A string that is 30.0 cm long and has a mass per...Ch. 17 - In the arrangement shown in Figure P17.14, an...Ch. 17 - Review. A sphere of mass M = 1.00 kg is supported...Ch. 17 - Review. A sphere of mass M is supported by a...Ch. 17 - Prob. 17PCh. 17 - Review. A solid copper object hangs at the bottom...Ch. 17 - The Bay of Fundy, Nova Scotia, has the highest...Ch. 17 - Prob. 20PCh. 17 - The fundamental frequency of an open organ pipe...Ch. 17 - Ever since seeing Figure 16.22 in the previous...Ch. 17 - An air column in a glass tube is open at one end...Ch. 17 - A shower stall has dimensions 86.0 cm 86.0 cm ...Ch. 17 - Prob. 25PCh. 17 - Prob. 26PCh. 17 - As shown in Figure P17.27, water is pumped into a...Ch. 17 - As shown in Figure P17.27, water is pumped into a...Ch. 17 - Prob. 29PCh. 17 - Why is the following situation impossible? A...Ch. 17 - Review. A student holds a tuning fork oscillating...Ch. 17 - Prob. 32PCh. 17 - Suppose a flutist plays a 523-Hz C note with first...Ch. 17 - Two strings are vibrating at the same frequency of...Ch. 17 - Prob. 35APCh. 17 - A 2.00-m-long wire having a mass of 0.100 kg is...Ch. 17 - Prob. 37APCh. 17 - You are working as an assistant to a landscape...Ch. 17 - Review. Consider the apparatus shown in Figure...Ch. 17 - Review. For the arrangement shown in Figure...Ch. 17 - Review. A loudspeaker at the front of a room and...Ch. 17 - Two speakers are driven by the same oscillator of...Ch. 17 - A standing wave is set up in a string of variable...Ch. 17 - Review. The top end of a yo-yo string is held...Ch. 17 - Prob. 45APCh. 17 - Prob. 46APCh. 17 - Review. A 12.0-kg object hangs in equilibrium from...Ch. 17 - Review. An object of mass m hangs in equilibrium...Ch. 17 - Two waves are described by the wave functions...Ch. 17 - Prob. 50CP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forward13.87 ... Interplanetary Navigation. The most efficient way to send a spacecraft from the earth to another planet is by using a Hohmann transfer orbit (Fig. P13.87). If the orbits of the departure and destination planets are circular, the Hohmann transfer orbit is an elliptical orbit whose perihelion and aphelion are tangent to the orbits of the two planets. The rockets are fired briefly at the depar- ture planet to put the spacecraft into the transfer orbit; the spacecraft then coasts until it reaches the destination planet. The rockets are then fired again to put the spacecraft into the same orbit about the sun as the destination planet. (a) For a flight from earth to Mars, in what direction must the rockets be fired at the earth and at Mars: in the direction of motion, or opposite the direction of motion? What about for a flight from Mars to the earth? (b) How long does a one- way trip from the the earth to Mars take, between the firings of the rockets? (c) To reach Mars from the…arrow_forwardNo chatgpt pls will upvotearrow_forward
- a cubic foot of argon at 20 degrees celsius is isentropically compressed from 1 atm to 425 KPa. What is the new temperature and density?arrow_forwardCalculate the variance of the calculated accelerations. The free fall height was 1753 mm. The measured release and catch times were: 222.22 800.00 61.11 641.67 0.00 588.89 11.11 588.89 8.33 588.89 11.11 588.89 5.56 586.11 2.78 583.33 Give in the answer window the calculated repeated experiment variance in m/s2.arrow_forwardNo chatgpt pls will upvotearrow_forward
- 2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward2-3. Consider the situation of the reflection of a pulse at the interface of two string described in the previous problem. In addition to the net disturbances being equal at the junction, the slope of the net disturbances must also be equal at the junction at all times. Given that p1 = 4.0 g/m, H2 = 9.0 g/m and Aj = 0.50 cm find 2. A, (Answer: -0.10 cm) and 3. Ay. (Answer: 0.40 cm)please I need to show all work step by step problems 2 and 3arrow_forwardFrom number 2 and 3 I just want to show all problems step by step please do not short cut look for formulaarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
What Are Sound Wave Properties? | Physics in Motion; Author: GPB Education;https://www.youtube.com/watch?v=GW6_U553sK8;License: Standard YouTube License, CC-BY