Chapter 1.6, Problem 1BGP

To determine

To explain: the domain and range of a function.

Explanation of Solution

The domain is the set of all possible  x values for the function to be difined.

For domain,

(i).The denominator of a rational function cannot be zero

(ii).The number under a square root sign must be positive 

Example:

Here is the graph of $y=\sqrt{x+4}$

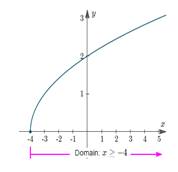
The domain of this function $x>-4$ , since $x$ cannot be less than $-4$ .

The range of a function is the complete set of all possible resulting values of the dependent variable, after substituted the domain.

1. The range of a function is possible  y - for the function to be defined.

Example:

Let’s return to the example above, $y=\sqrt{x+4}$

The curve is either on or above the horizontal axis. The range in this case is  $y\ge 0$ .

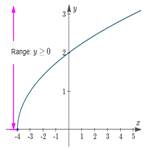
The curve goes on forever vertically, beyond what is shown on the graph, so the range is all non-negative values of  y .