VECTOR MECHANICS FOR ENGINEERS W/CON >B
12th Edition
ISBN: 9781260804638
Author: BEER
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13.2, Problem 13.117P
Using the answers obtained in Prob. 13.108, show that the intended circular orbit and the resulting elliptic orbit intersect at the ends of the minor axis of the elliptic orbit.
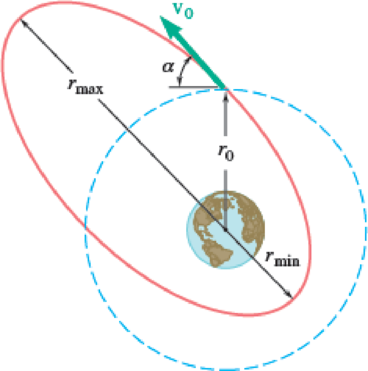
13.108 A satellite is projected into space with a velocity v0 at a distance r0 from the center of the earth by the last stage of its launching rocket. The velocity v0 was designed to send the satellite into a circular orbit of radius r0. However, owing to a malfunction of control, the satellite is not projected horizontally but at an angle α with the horizontal and, as a result, is propelled into an elliptic orbit. Determine the maximum and minimum values of the distance from the center of the earth to the satellite.
Fig. P13.108
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please answer the following question. Include all work and plase explain. Graphs are provided below. "Consider the Mg (Magnesium) - Ni (Nickel) phase diagram shown below. This phase diagram contains two eutectic reactions and two intermediate phases (Mg2Ni and MgNi2). At a temperature of 505oC, determine what the composition of an alloy would need to be to contain a mass fraction of 0.20 Mg and 0.80 Mg2Ni."
The triangular plate, having a 90∘∘ angle at AA, supports the load PP = 370 lblb as shown in (Figure 1).
Design a 4-bar linkage to carry the body in Figure 1 through the two positions P1 and P2 at the
angles shown in the figure. Use analytical synthesis with the free choice values z = 1.075, q=
210°, ß2 = −27° for left side and s = 1.24, y= 74°, ½ = − 40° for right side.
φ
1.236
P2
147.5°
210°
2.138
P1
Figure 1
X
Chapter 13 Solutions
VECTOR MECHANICS FOR ENGINEERS W/CON >B
Ch. 13.1 - Block A is traveling with a speed v0 on a smooth...Ch. 13.1 - A 400-kg satellite is placed in a circular orbit...Ch. 13.1 - A 0.5-lb stone is dropped down the bottomless pit...Ch. 13.1 - A baseball player hits a 5.1-oz baseball with an...Ch. 13.1 - A 500-kg communications satellite is in a circular...Ch. 13.1 - Prob. 13.5PCh. 13.1 - In an ore-mixing operation, a bucket full of ore...Ch. 13.1 - Determine the maximum theoretical speed that may...Ch. 13.1 - A 2000-kg automobile starts from rest at point A...Ch. 13.1 - An athlete is holding 30 lb of weights at a height...
Ch. 13.1 - A 1.4-kg model rocket is launched vertically from...Ch. 13.1 - Packages are thrown down an incline at A with a...Ch. 13.1 - A package is thrown down an incline at A with a...Ch. 13.1 - Boxes are transported by a conveyor belt with a...Ch. 13.1 - Boxes are transported by a conveyor belt with a...Ch. 13.1 - A 1200-kg trailer is hitched to a 1400-kg car. The...Ch. 13.1 - Prob. 13.16PCh. 13.1 - Prob. 13.17PCh. 13.1 - The subway train shown is traveling at a speed of...Ch. 13.1 - A 5000-lb truck is being used to lift a 1000-lb...Ch. 13.1 - The system shown is at rest when a constant 30-lb...Ch. 13.1 - Car B is towing car A at a constant speed of 10...Ch. 13.1 - The motor applies a constant downward force F =...Ch. 13.1 - The motor applies a constant downward force F to...Ch. 13.1 - Two blocks A and B, of mass 4 kg and 5 kg,...Ch. 13.1 - Four 15-kg packages are placed as shown on a...Ch. 13.1 - A 3-kg block rests on top of a 2-kg block...Ch. 13.1 - Solve Prob. 13.26, assuming that the 2-kg block is...Ch. 13.1 - Prob. 13.28PCh. 13.1 - A 7.5-lb collar is released from rest in the...Ch. 13.1 - A 10-kg block is attached to spring A and...Ch. 13.1 - A 5-kg collar A is at rest on top of, but not...Ch. 13.1 - Prob. 13.32PCh. 13.1 - Prob. 13.33PCh. 13.1 - Two types of energy-absorbing fenders designed to...Ch. 13.1 - Prob. 13.35PCh. 13.1 - Prob. 13.36PCh. 13.1 - Prob. 13.37PCh. 13.1 - Prob. 13.38PCh. 13.1 - Prob. 13.39PCh. 13.1 - The sphere at A is given a downward velocity v0...Ch. 13.1 - A bag is gently pushed off the top of a wall at A...Ch. 13.1 - A roller coaster starts from rest at A, rolls down...Ch. 13.1 - In Prob. 13.42, determine the range of values of h...Ch. 13.1 - A small block slides at a speed v on a horizontal...Ch. 13.1 - Prob. 13.45PCh. 13.1 - Prob. 13.46PCh. 13.1 - Prob. 13.47PCh. 13.1 - Prob. 13.48PCh. 13.1 - Prob. 13.49PCh. 13.1 - Prob. 13.50PCh. 13.1 - A 1400-kg automobile starts from rest and travels...Ch. 13.1 - The frictional resistance of a ship is known to...Ch. 13.1 - Prob. 13.53PCh. 13.1 - The elevator E has a weight of 6600 lb when fully...Ch. 13.2 - Two small balls A and B with masses 2m and m,...Ch. 13.2 - Prob. 13.3CQCh. 13.2 - Prob. 13.55PCh. 13.2 - A loaded railroad car of mass m is rolling at a...Ch. 13.2 - A 750-g collar can slide along the horizontal rod...Ch. 13.2 - A 2-lb collar C may slide without friction along a...Ch. 13.2 - Solve Prob. 13.58 assuming the spring CD has been...Ch. 13.2 - A 500-g collar can slide without friction on the...Ch. 13.2 - For the adapted shuffleboard device in Prob 13.28,...Ch. 13.2 - An elastic cable is to be designed for bungee...Ch. 13.2 - It is shown in mechanics of materials that the...Ch. 13.2 - A 1.2-kg collar can slide along the rod shown. It...Ch. 13.2 - A 500-g collar can slide without friction along...Ch. 13.2 - A thin circular rod is supported in a vertical...Ch. 13.2 - Prob. 13.67PCh. 13.2 - A spring is used to stop a 50-kg package that is...Ch. 13.2 - Prob. 13.69PCh. 13.2 - A roller coaster starts from rest at A, rolls down...Ch. 13.2 - A roller coaster starts from rest at A, rolls down...Ch. 13.2 - A 1-lb collar is attached to a spring and slides...Ch. 13.2 - A 10-lb collar is attached to a spring and slides...Ch. 13.2 - Prob. 13.74PCh. 13.2 - Prob. 13.75PCh. 13.2 - A small package of weight W is projected into a...Ch. 13.2 - Prob. 13.77PCh. 13.2 - The pendulum shown is given an initial speed v0 at...Ch. 13.2 - Prove that a force F(x, y, z) is conservative if,...Ch. 13.2 - The force F = (yzi + zxj + xyk)/xyz acts on the...Ch. 13.2 - Prob. 13.81PCh. 13.2 - Prob. 13.82PCh. 13.2 - Prob. 13.83PCh. 13.2 - Prob. 13.84PCh. 13.2 - Prob. 13.85PCh. 13.2 - A satellite describes an elliptic orbit of minimum...Ch. 13.2 - While describing a circular orbit 200 mi above the...Ch. 13.2 - How much energy per pound should be imparted to a...Ch. 13.2 - Knowing that the velocity of an experimental space...Ch. 13.2 - Prob. 13.90PCh. 13.2 - Prob. 13.91PCh. 13.2 - (a) Show that, by setting r = R + y in the...Ch. 13.2 - Collar A has a mass of 3 kg and is attached to a...Ch. 13.2 - Collar A has a mass of 3 kg and is attached to a...Ch. 13.2 - A governor is designed so that the valve of...Ch. 13.2 - A 1.5-lb ball that can slide on a horizontal...Ch. 13.2 - A 1.5-lb ball that can slide on a horizontal...Ch. 13.2 - Using the principles of conservation of energy and...Ch. 13.2 - Prob. 13.99PCh. 13.2 - A spacecraft is describing an elliptic orbit of...Ch. 13.2 - While describing a circular orbit, 185 mi above...Ch. 13.2 - Prob. 13.102PCh. 13.2 - Prob. 13.103PCh. 13.2 - Prob. 13.104PCh. 13.2 - Prob. 13.105PCh. 13.2 - Prob. 13.106PCh. 13.2 - Prob. 13.107PCh. 13.2 - Prob. 13.108PCh. 13.2 - Prob. 13.109PCh. 13.2 - A space vehicle is in a circular orbit at an...Ch. 13.2 - Prob. 13.111PCh. 13.2 - Show that the values vA and vP of the speed of an...Ch. 13.2 - Show that the total energy E of an earth satellite...Ch. 13.2 - A space probe describes a circular orbit of radius...Ch. 13.2 - Prob. 13.115PCh. 13.2 - A spacecraft of mass m describes a circular orbit...Ch. 13.2 - Using the answers obtained in Prob. 13.108, show...Ch. 13.2 - Prob. 13.118PCh. 13.3 - A large insect impacts the front windshield of a...Ch. 13.3 - The expected damages associated with two types of...Ch. 13.3 - Prob. 13.1IMDCh. 13.3 - Prob. 13.2IMDCh. 13.3 - Prob. 13.3IMDCh. 13.3 - Prob. 13.4IMDCh. 13.3 - Prob. 13.5IMDCh. 13.3 - A 35 000-Mg ocean liner has an initial velocity of...Ch. 13.3 - A 2500-lb automobile is moving at a speed of 60...Ch. 13.3 - Prob. 13.121PCh. 13.3 - A truck is hauling a 300-kg log out of a ditch...Ch. 13.3 - The coefficients of friction between the load and...Ch. 13.3 - Steep safety ramps are built beside mountain...Ch. 13.3 - Prob. 13.125PCh. 13.3 - The 18 000-kg F-35B uses thrust vectoring to allow...Ch. 13.3 - Prob. 13.127PCh. 13.3 - Prob. 13.128PCh. 13.3 - The subway train shown is traveling at a speed of...Ch. 13.3 - The subway train shown is traveling at a speed of...Ch. 13.3 - A tractor-trailer rig with a 2000-kg tractor, a...Ch. 13.3 - The motor applies a constant downward force F =...Ch. 13.3 - An 8-kg cylinder C rests on a 4-kg platform A...Ch. 13.3 - An estimate of the expected load on...Ch. 13.3 - A 60-g model rocket is fired vertically. The...Ch. 13.3 - A 12-lb block, which can slide on a frictionless...Ch. 13.3 - A crash test is performed between an SUV A and a...Ch. 13.3 - Prob. 13.138PCh. 13.3 - Prob. 13.139PCh. 13.3 - Prob. 13.140PCh. 13.3 - The triple jump is a track-and-field event in...Ch. 13.3 - The last segment of the triple jump...Ch. 13.3 - The design for a new cementless hip implant is to...Ch. 13.3 - A 28-g steel-jacketed bullet is fired with a...Ch. 13.3 - A 120-ton tugboat is moving at 6 ft/s with a slack...Ch. 13.3 - At an intersection, car B was traveling south and...Ch. 13.3 - The 650-kg hammer of a drop-hammer pile driver...Ch. 13.3 - Prob. 13.148PCh. 13.3 - Bullet B weighs 0.5 oz and blocks A and C both...Ch. 13.3 - A 180-lb man and a 120-lb woman stand at opposite...Ch. 13.3 - A 75-g ball is projected from a height of 1.6 m...Ch. 13.3 - A ballistic pendulum is used to measure the speed...Ch. 13.3 - Prob. 13.153PCh. 13.3 - Prob. 13.154PCh. 13.4 - A 5-kg ball A strikes a 1-kg ball B that is...Ch. 13.4 - A sphere with a speed v0 rebounds after striking a...Ch. 13.4 - Prob. 13.7IMDCh. 13.4 - Prob. 13.8IMDCh. 13.4 - A 10-kg ball A moving horizontally at 12 m/s...Ch. 13.4 - Prob. 13.10IMDCh. 13.4 - Two steel blocks slide without friction on a...Ch. 13.4 - Prob. 13.156PCh. 13.4 - Prob. 13.157PCh. 13.4 - Prob. 13.158PCh. 13.4 - To apply shock loading to an artillery shell, a...Ch. 13.4 - Packages in an automobile parts supply house are...Ch. 13.4 - Three steel spheres of equal mass are suspended...Ch. 13.4 - At an amusement park, there are 200-kg bumper cars...Ch. 13.4 - At an amusement park there are 200-kg bumper cars...Ch. 13.4 - Prob. 13.164PCh. 13.4 - Prob. 13.165PCh. 13.4 - A 600-g ball A is moving with a velocity of...Ch. 13.4 - Two identical hockey pucks are moving on a hockey...Ch. 13.4 - A billiard player wishes to have ball A hit ball B...Ch. 13.4 - Prob. 13.169PCh. 13.4 - Prob. 13.170PCh. 13.4 - A girl throws a ball at an inclined wall from a...Ch. 13.4 - Prob. 13.172PCh. 13.4 - From experimental tests, smaller boulders tend to...Ch. 13.4 - Prob. 13.174PCh. 13.4 - A 1-kg block B is moving with a velocity v0 of...Ch. 13.4 - A 0.25-lb ball thrown with a horizontal velocity...Ch. 13.4 - After having been pushed by an airline employee,...Ch. 13.4 - Prob. 13.178PCh. 13.4 - A 5-kg sphere is dropped from a height of y = 2 m...Ch. 13.4 - A 5-kg sphere is dropped from a height of y = 3 m...Ch. 13.4 - Prob. 13.181PCh. 13.4 - Block A is released from rest and slides down the...Ch. 13.4 - A 23.1-kg sphere A of radius 90 mm moving with a...Ch. 13.4 - A test machine that kicks soccer balls has a 5-lb...Ch. 13.4 - Ball B is hanging from an inextensible cord. An...Ch. 13.4 - A 70-g ball B dropped from a height h0 = 1.5 m...Ch. 13.4 - A 2-kg sphere moving to the right with a velocity...Ch. 13.4 - When the rope is at an angle of = 30, the 1-lb...Ch. 13.4 - When the rope is at an angle of = 30, the 1-kg...Ch. 13 - A 34,000-lb airplane lands on an aircraft carrier...Ch. 13 - There has been renewed interest in pneumatic tube...Ch. 13 - Prob. 13.192RPCh. 13 - A section of track for a roller coaster consists...Ch. 13 - Two identical 40-lb curling stones have diameters...Ch. 13 - A 300-g block is released from rest after a spring...Ch. 13 - A kicking-simulation attachment goes on the front...Ch. 13 - A 625-g basketball and a 58.5-g tennis ball are...Ch. 13 - Prob. 13.198RPCh. 13 - A 2-kg ball B is traveling horizontally at 10 m/s...Ch. 13 - A 2-kg block A is pushed up against a spring...Ch. 13 - The 2-lb ball at A is suspended by an inextensible...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Design a 4-bar linkage to carry the body in Figure 1 through the two positions P1 and P2 at the angles shown in the figure. Use analytical synthesis with the free choice values z = 1.075, q= 210°, B₂ = −27° for left side and s = 1.24, y= 74°, ½ = − 40° for right side. 1.236 P2 147.5° 210° P1 Figure 1 2.138 Xarrow_forwardcan you explain how in a coordinate frame transformation: v = {v_n}^T {n-hat} and then it was found that {n-hat} = [C]^T {b-hat} so v_n = {v_n}^T [C]^T {b-hat}, how does that equation go from that to this --> v_n = [C]^T v_barrow_forward6) If (k = 0,7 cm) find Imax for figure below. 225mm 100mm ثلاثاء. 100mm 150mm 75mm Ans: Tmax=45:27 N/cm F-400 Narrow_forward
- The man has a weight W and stands halfway along the beam. The beam is not smooth, but the planes at A and B are smooth (and plane A is horizontal). Determine the magnitude of the tension in the cord in terms of W and θ.arrow_forwardDetermine the reactions at the two supports for this plate. Express the reactions in Cartesian vector form.arrow_forwardDetermine the magnitudes of the reactions at the supports for this large plate.arrow_forward
- Only expert should solvearrow_forwardA 15 cm-OD pipe is buried with its centerline 1.25 m below the surface of the ground [k of soil is 0.35 W/(m K)]. An oil having a density of 800 kg/m³ and a specific heat of 2.1 kJ/(kg K) flows in the pipe at 5.6 L/s. Assuming a ground surface temperature of 5°C and a pipe wall temperature of 95°C, estimate the length of pipe in which the oil temperature decreases by 5.5°C. + Tε = 5ºC Z= 1.25 m D= 15 cm 7p=95°Carrow_forwardFind the solution of the following Differential Equations 1) 4y+y=0, y(0)=2, y'(0) = 0. 2) y+y=0, y(0) = A, y'(0) = B. 3) "+2y'-8y=0, y(0)=1, y'(0)=8. 4) y"-2y-3y=0, y(0)=1, y'(0)=7. 5) y"-ky' =0, y(0)=2, y'(0) =k. 6) y+ky'-2k2y=0, y(0)=2, y'(0) = 2k. 7) y'+4y=0, y(0)=2.8 y+y-17sin(21) y(0)=-1. 9) y-y'-6y=0, y(0)=6. y'(0)=13. 10) y-y=0, 11) y"-4y+4y=0, y(0)=4, y'(0) = 0. y(0) = 2.1, y'(0)=3.9 12) y+2y+2y=0, y(0)=1, y'(0)=-3. 13) "+7y+12y=21e", y(0)=3.5, y'(0)=-10. 14) "+9y=10e", y(0)=0. y'(0) = 0. 15) y+3y+2.25y=91³ +64. y(0)=1, y'(0) = 31.5 16) "-6y+5y= 29 cos(21), y(0)=3.2, y'(0) = 6.2 17) y+2y+2y=0, y(0)=0, y'(0)=1. 18) y+2y+17y=0, y(0)=0, y'(0)=12. 19) y-4y+5y=0, y(0)-1, y'(0) 2. 20) 9y-6y+y=0. y(0)=3, y'(0)=1. 21) -2y+10y=0, y(0)=3, y'(0)=3. 22) 4y-4y+37y=0, (0) 3. y(0) 1.5 23) 4y-8y+5y=0, (0)-0, y(0) 1. 24) y+y+1.25y=0, y(0) 1. y'(0) -0.5 25) y+y=2 cos(1). y(0) 2. y'(0) = 0. 26) -4y+3y=0, (0)-3, y'(0) = 7. 27) y+2y+y=e", y(0)-0. y'(0) = 0. 29) 28) y+2y-3y-10sinh(2),…arrow_forward
- Note: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting appreciate your time and effort!. Question:arrow_forward4. Block A and B are two different pieces of wood. Determine the minimum dimension for "a", if the shear stress of the wood is 50Mpa. The thickness of the wood is 30cm. 600N Aarrow_forward1. Determine the reaction force at A. 60 kN 5 B 1 m 1 m- -1 m 4 3 m 30 kN marrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Dynamics - Lesson 1: Introduction and Constant Acceleration Equations; Author: Jeff Hanson;https://www.youtube.com/watch?v=7aMiZ3b0Ieg;License: Standard YouTube License, CC-BY