McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 13, Problem 15CUR
To determine
To prove: If the ray that bisects an
Expert Solution & Answer
Explanation of Solution
Given information: A ray that bisects an angle of a triangle is perpendicular to the side that it intersects.
Proof:
Draw the figure of a triangle ABC according to the given conditions as shown below.
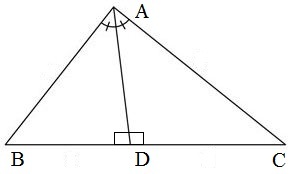
Here, AD⊥BC and BD=DC .
In ΔABD and ΔADC ,
BD = DC(given)AD=AD(common)∠BAD=∠DAC(ray bisects angle)
It can be observed that two sides and an angle of one triangle is equal to the two sides and an angle of other triangle. So, by SAS theorem both triangles are congruent.
ΔABD≅ΔADC
By corresponding part of congruent triangle, AB=AC .
Hence, if the ray that bisects an angle of a triangle is perpendicular to the side that it intersects, then the triangle is an isosceles triangle.
Chapter 13 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 13.1 - Prob. 1CECh. 13.1 - Prob. 2CECh. 13.1 - Prob. 3CECh. 13.1 - Prob. 4CECh. 13.1 - Prob. 5CECh. 13.1 - Prob. 6CECh. 13.1 - Prob. 7CECh. 13.1 - Prob. 8CECh. 13.1 - Prob. 9CECh. 13.1 - Prob. 10CE
Ch. 13.1 - Prob. 11CECh. 13.1 - Prob. 12CECh. 13.1 - Prob. 1WECh. 13.1 - Prob. 2WECh. 13.1 - Prob. 3WECh. 13.1 - Prob. 4WECh. 13.1 - Prob. 5WECh. 13.1 - Prob. 6WECh. 13.1 - Prob. 7WECh. 13.1 - Prob. 8WECh. 13.1 - Prob. 9WECh. 13.1 - Prob. 10WECh. 13.1 - Prob. 11WECh. 13.1 - Prob. 12WECh. 13.1 - Prob. 13WECh. 13.1 - Prob. 14WECh. 13.1 - Prob. 15WECh. 13.1 - Prob. 16WECh. 13.1 - Prob. 17WECh. 13.1 - Prob. 18WECh. 13.1 - Prob. 19WECh. 13.1 - Prob. 20WECh. 13.1 - Prob. 21WECh. 13.1 - Prob. 22WECh. 13.1 - Prob. 23WECh. 13.1 - Prob. 24WECh. 13.1 - Prob. 25WECh. 13.1 - Prob. 26WECh. 13.1 - Prob. 27WECh. 13.1 - Prob. 28WECh. 13.1 - Prob. 29WECh. 13.1 - Prob. 30WECh. 13.1 - Prob. 31WECh. 13.1 - Prob. 32WECh. 13.1 - Prob. 33WECh. 13.1 - Prob. 34WECh. 13.1 - Prob. 35WECh. 13.1 - Prob. 36WECh. 13.1 - Prob. 37WECh. 13.1 - Prob. 38WECh. 13.1 - Prob. 39WECh. 13.1 - Prob. 40WECh. 13.1 - Prob. 41WECh. 13.1 - Prob. 42WECh. 13.1 - Prob. 43WECh. 13.1 - Prob. 44WECh. 13.1 - Prob. 45WECh. 13.1 - Prob. 3ECh. 13.2 - Prob. 1CECh. 13.2 - Prob. 2CECh. 13.2 - Prob. 3CECh. 13.2 - Prob. 4CECh. 13.2 - Prob. 5CECh. 13.2 - Prob. 6CECh. 13.2 - Prob. 7CECh. 13.2 - Prob. 8CECh. 13.2 - Prob. 1WECh. 13.2 - Prob. 2WECh. 13.2 - Prob. 3WECh. 13.2 - Prob. 4WECh. 13.2 - Prob. 5WECh. 13.2 - Prob. 6WECh. 13.2 - Prob. 7WECh. 13.2 - Prob. 8WECh. 13.2 - Prob. 9WECh. 13.2 - Prob. 10WECh. 13.2 - Prob. 11WECh. 13.2 - Prob. 12WECh. 13.2 - Prob. 13WECh. 13.2 - Prob. 14WECh. 13.2 - Prob. 15WECh. 13.2 - Prob. 16WECh. 13.2 - Prob. 17WECh. 13.2 - Prob. 18WECh. 13.2 - Prob. 19WECh. 13.2 - Prob. 20WECh. 13.2 - Prob. 21WECh. 13.2 - Prob. 22WECh. 13.2 - Prob. 23WECh. 13.2 - Prob. 24WECh. 13.2 - Prob. 25WECh. 13.2 - Prob. 26WECh. 13.2 - Prob. 27WECh. 13.2 - Prob. 28WECh. 13.2 - Prob. 29WECh. 13.2 - Prob. 30WECh. 13.2 - Prob. 31WECh. 13.2 - Prob. 32WECh. 13.2 - Prob. 33WECh. 13.2 - Prob. 34WECh. 13.2 - Prob. 1ARCh. 13.2 - Prob. 2ARCh. 13.2 - Prob. 3ARCh. 13.2 - Prob. 4ARCh. 13.2 - Prob. 5ARCh. 13.2 - Prob. 6ARCh. 13.2 - Prob. 7ARCh. 13.2 - Prob. 8ARCh. 13.2 - Prob. 9ARCh. 13.2 - Prob. 10ARCh. 13.2 - Prob. 11ARCh. 13.2 - Prob. 12ARCh. 13.2 - Prob. 13ARCh. 13.2 - Prob. 14ARCh. 13.2 - Prob. 15ARCh. 13.2 - Prob. 16ARCh. 13.2 - Prob. 17ARCh. 13.2 - Prob. 18ARCh. 13.2 - Prob. 19ARCh. 13.2 - Prob. 20ARCh. 13.2 - Prob. 21ARCh. 13.2 - Prob. 22ARCh. 13.2 - Prob. 23ARCh. 13.2 - Prob. 24ARCh. 13.3 - Prob. 1CECh. 13.3 - Prob. 2CECh. 13.3 - Prob. 3CECh. 13.3 - Prob. 4CECh. 13.3 - Prob. 5CECh. 13.3 - Prob. 6CECh. 13.3 - Prob. 7CECh. 13.3 - Prob. 8CECh. 13.3 - Prob. 9CECh. 13.3 - Prob. 10CECh. 13.3 - Prob. 11CECh. 13.3 - Prob. 1WECh. 13.3 - Prob. 2WECh. 13.3 - Prob. 3WECh. 13.3 - Prob. 4WECh. 13.3 - Prob. 5WECh. 13.3 - Prob. 6WECh. 13.3 - Prob. 7WECh. 13.3 - Prob. 8WECh. 13.3 - Prob. 9WECh. 13.3 - Prob. 10WECh. 13.3 - Prob. 11WECh. 13.3 - Prob. 12WECh. 13.3 - Prob. 13WECh. 13.3 - Prob. 14WECh. 13.3 - Prob. 15WECh. 13.3 - Prob. 16WECh. 13.3 - Prob. 17WECh. 13.3 - Prob. 18WECh. 13.3 - Prob. 19WECh. 13.3 - Prob. 20WECh. 13.3 - Prob. 21WECh. 13.3 - Prob. 22WECh. 13.3 - Prob. 23WECh. 13.4 - Prob. 1CECh. 13.4 - Prob. 2CECh. 13.4 - Prob. 3CECh. 13.4 - Prob. 4CECh. 13.4 - Prob. 5CECh. 13.4 - Prob. 6CECh. 13.4 - Prob. 7CECh. 13.4 - Prob. 8CECh. 13.4 - Prob. 1WECh. 13.4 - Prob. 2WECh. 13.4 - Prob. 3WECh. 13.4 - Prob. 4WECh. 13.4 - Prob. 5WECh. 13.4 - Prob. 6WECh. 13.4 - Prob. 7WECh. 13.4 - Prob. 8WECh. 13.4 - Prob. 9WECh. 13.4 - Prob. 10WECh. 13.4 - Prob. 11WECh. 13.4 - Prob. 12WECh. 13.4 - Prob. 13WECh. 13.4 - Prob. 14WECh. 13.4 - Prob. 15WECh. 13.4 - Prob. 16WECh. 13.4 - Prob. 17WECh. 13.4 - Prob. 18WECh. 13.4 - Prob. 19WECh. 13.4 - Prob. 20WECh. 13.4 - Prob. 21WECh. 13.4 - Prob. 22WECh. 13.4 - Prob. 23WECh. 13.4 - Prob. 24WECh. 13.4 - Prob. 25WECh. 13.4 - Prob. 26WECh. 13.4 - Prob. 27WECh. 13.4 - Prob. 28WECh. 13.4 - Prob. 29WECh. 13.4 - Prob. 30WECh. 13.4 - Prob. 31WECh. 13.4 - Prob. 32WECh. 13.4 - Prob. 33WECh. 13.4 - Prob. 34WECh. 13.4 - Prob. 1MRECh. 13.4 - Prob. 2MRECh. 13.4 - Prob. 3MRECh. 13.4 - Prob. 4MRECh. 13.4 - Prob. 5MRECh. 13.4 - Prob. 6MRECh. 13.4 - Prob. 7MRECh. 13.4 - Prob. 8MRECh. 13.4 - Prob. 9MRECh. 13.4 - Prob. 10MRECh. 13.4 - Prob. 11MRECh. 13.4 - Prob. 12MRECh. 13.5 - Prob. 1CECh. 13.5 - Prob. 2CECh. 13.5 - Prob. 3CECh. 13.5 - Prob. 4CECh. 13.5 - Prob. 5CECh. 13.5 - Prob. 6CECh. 13.5 - Prob. 7CECh. 13.5 - Prob. 8CECh. 13.5 - Prob. 9CECh. 13.5 - Prob. 10CECh. 13.5 - Prob. 1WECh. 13.5 - Prob. 2WECh. 13.5 - Prob. 3WECh. 13.5 - Prob. 4WECh. 13.5 - Prob. 5WECh. 13.5 - Prob. 6WECh. 13.5 - Prob. 7WECh. 13.5 - Prob. 8WECh. 13.5 - Prob. 9WECh. 13.5 - Prob. 10WECh. 13.5 - Prob. 11WECh. 13.5 - Prob. 12WECh. 13.5 - Prob. 13WECh. 13.5 - Prob. 14WECh. 13.5 - Prob. 15WECh. 13.5 - Prob. 16WECh. 13.5 - Prob. 17WECh. 13.5 - Prob. 18WECh. 13.5 - Prob. 19WECh. 13.5 - Prob. 20WECh. 13.5 - Prob. 21WECh. 13.5 - Prob. 22WECh. 13.5 - Prob. 23WECh. 13.5 - Prob. 24WECh. 13.5 - Prob. 1ST1Ch. 13.5 - Prob. 2ST1Ch. 13.5 - Prob. 3ST1Ch. 13.5 - Prob. 4ST1Ch. 13.5 - Prob. 5ST1Ch. 13.5 - Prob. 6ST1Ch. 13.5 - Prob. 7ST1Ch. 13.5 - Prob. 8ST1Ch. 13.5 - Prob. 9ST1Ch. 13.5 - Prob. 10ST1Ch. 13.5 - Prob. 11ST1Ch. 13.5 - Prob. 12ST1Ch. 13.5 - Prob. 13ST1Ch. 13.5 - Prob. 14ST1Ch. 13.5 - Prob. 15ST1Ch. 13.6 - Prob. 1CECh. 13.6 - Prob. 2CECh. 13.6 - Prob. 3CECh. 13.6 - Prob. 4CECh. 13.6 - Prob. 5CECh. 13.6 - Prob. 6CECh. 13.6 - Prob. 7CECh. 13.6 - Prob. 8CECh. 13.6 - Prob. 9CECh. 13.6 - Prob. 10CECh. 13.6 - Prob. 11CECh. 13.6 - Prob. 12CECh. 13.6 - Prob. 13CECh. 13.6 - Prob. 1WECh. 13.6 - Prob. 2WECh. 13.6 - Prob. 3WECh. 13.6 - Prob. 4WECh. 13.6 - Prob. 5WECh. 13.6 - Prob. 6WECh. 13.6 - Prob. 7WECh. 13.6 - Prob. 8WECh. 13.6 - Prob. 9WECh. 13.6 - Prob. 10WECh. 13.6 - Prob. 11WECh. 13.6 - Prob. 12WECh. 13.6 - Prob. 13WECh. 13.6 - Prob. 14WECh. 13.6 - Prob. 15WECh. 13.6 - Prob. 16WECh. 13.6 - Prob. 17WECh. 13.6 - Prob. 18WECh. 13.6 - Prob. 19WECh. 13.6 - Prob. 20WECh. 13.6 - Prob. 21WECh. 13.6 - Prob. 22WECh. 13.6 - Prob. 23WECh. 13.6 - Prob. 24WECh. 13.6 - Prob. 25WECh. 13.6 - Prob. 26WECh. 13.6 - Prob. 27WECh. 13.6 - Prob. 28WECh. 13.6 - Prob. 29WECh. 13.6 - Prob. 30WECh. 13.6 - Prob. 31WECh. 13.6 - Prob. 32WECh. 13.6 - Prob. 33WECh. 13.6 - Prob. 34WECh. 13.6 - Prob. 35WECh. 13.6 - Prob. 36WECh. 13.6 - Prob. 37WECh. 13.6 - Prob. 38WECh. 13.6 - Prob. 39WECh. 13.6 - Prob. 1CCh. 13.7 - Prob. 1CECh. 13.7 - Prob. 2CECh. 13.7 - Prob. 3CECh. 13.7 - Prob. 4CECh. 13.7 - Prob. 5CECh. 13.7 - Prob. 6CECh. 13.7 - Prob. 7CECh. 13.7 - Prob. 8CECh. 13.7 - Prob. 9CECh. 13.7 - Prob. 10CECh. 13.7 - Prob. 11CECh. 13.7 - Prob. 12CECh. 13.7 - Prob. 13CECh. 13.7 - Prob. 14CECh. 13.7 - Prob. 1WECh. 13.7 - Prob. 2WECh. 13.7 - Prob. 3WECh. 13.7 - Prob. 4WECh. 13.7 - Prob. 5WECh. 13.7 - Prob. 6WECh. 13.7 - Prob. 7WECh. 13.7 - Prob. 8WECh. 13.7 - Prob. 9WECh. 13.7 - Prob. 10WECh. 13.7 - Prob. 11WECh. 13.7 - Prob. 12WECh. 13.7 - Prob. 13WECh. 13.7 - Prob. 14WECh. 13.7 - Prob. 15WECh. 13.7 - Prob. 16WECh. 13.7 - Prob. 17WECh. 13.7 - Prob. 18WECh. 13.7 - Prob. 19WECh. 13.7 - Prob. 20WECh. 13.7 - Prob. 21WECh. 13.7 - Prob. 22WECh. 13.7 - Prob. 23WECh. 13.7 - Prob. 24WECh. 13.7 - Prob. 25WECh. 13.7 - Prob. 26WECh. 13.7 - Prob. 27WECh. 13.7 - Prob. 28WECh. 13.7 - Prob. 29WECh. 13.7 - Prob. 30WECh. 13.7 - Prob. 31WECh. 13.7 - Prob. 32WECh. 13.7 - Prob. 33WECh. 13.7 - Prob. 34WECh. 13.7 - Prob. 35WECh. 13.7 - Prob. 36WECh. 13.7 - Prob. 37WECh. 13.7 - Prob. 38WECh. 13.7 - Prob. 39WECh. 13.8 - Prob. 1CECh. 13.8 - Prob. 2CECh. 13.8 - Prob. 3CECh. 13.8 - Prob. 4CECh. 13.8 - Prob. 5CECh. 13.8 - Prob. 6CECh. 13.8 - Prob. 1WECh. 13.8 - Prob. 2WECh. 13.8 - Prob. 3WECh. 13.8 - Prob. 4WECh. 13.8 - Prob. 5WECh. 13.8 - Prob. 6WECh. 13.8 - Prob. 7WECh. 13.8 - Prob. 8WECh. 13.8 - Prob. 9WECh. 13.8 - Prob. 10WECh. 13.8 - Prob. 11WECh. 13.8 - Prob. 12WECh. 13.8 - Prob. 13WECh. 13.9 - Prob. 1CECh. 13.9 - Prob. 2CECh. 13.9 - Prob. 3CECh. 13.9 - Prob. 4CECh. 13.9 - Prob. 5CECh. 13.9 - Prob. 1WECh. 13.9 - Prob. 2WECh. 13.9 - Prob. 3WECh. 13.9 - Prob. 4WECh. 13.9 - Prob. 5WECh. 13.9 - Prob. 6WECh. 13.9 - Prob. 7WECh. 13.9 - Prob. 8WECh. 13.9 - Prob. 9WECh. 13.9 - Prob. 10WECh. 13.9 - Prob. 11WECh. 13.9 - Prob. 12WECh. 13.9 - Prob. 13WECh. 13.9 - Prob. 14WECh. 13.9 - Prob. 1ST2Ch. 13.9 - Prob. 2ST2Ch. 13.9 - Prob. 3ST2Ch. 13.9 - Prob. 4ST2Ch. 13.9 - Prob. 5ST2Ch. 13.9 - Prob. 6ST2Ch. 13.9 - Prob. 7ST2Ch. 13.9 - Prob. 8ST2Ch. 13.9 - Prob. 9ST2Ch. 13.9 - Prob. 1AECh. 13.9 - Prob. 2AECh. 13.9 - Prob. 3AECh. 13.9 - Prob. 4AECh. 13.9 - Prob. 1BECh. 13.9 - Prob. 2BECh. 13.9 - Prob. 3BECh. 13.9 - Prob. 4BECh. 13.9 - Prob. 5BECh. 13.9 - Prob. 6BECh. 13.9 - Prob. 7BECh. 13.9 - Prob. 8BECh. 13.9 - Prob. 9BECh. 13.9 - Prob. 10BECh. 13.9 - Prob. 11BECh. 13.9 - Prob. 12BECh. 13.9 - Prob. 13BECh. 13.9 - Prob. 14BECh. 13.9 - Prob. 15BECh. 13.9 - Prob. 16BECh. 13 - Prob. 1CRCh. 13 - Prob. 2CRCh. 13 - Prob. 3CRCh. 13 - Prob. 4CRCh. 13 - Prob. 5CRCh. 13 - Prob. 6CRCh. 13 - Prob. 7CRCh. 13 - Prob. 8CRCh. 13 - Prob. 9CRCh. 13 - Prob. 10CRCh. 13 - Prob. 11CRCh. 13 - Prob. 12CRCh. 13 - Prob. 13CRCh. 13 - Prob. 14CRCh. 13 - Prob. 15CRCh. 13 - Prob. 16CRCh. 13 - Prob. 17CRCh. 13 - Prob. 18CRCh. 13 - Prob. 19CRCh. 13 - Prob. 20CRCh. 13 - Prob. 21CRCh. 13 - Prob. 22CRCh. 13 - Prob. 23CRCh. 13 - Prob. 24CRCh. 13 - Prob. 25CRCh. 13 - Prob. 1CTCh. 13 - Prob. 2CTCh. 13 - Prob. 3CTCh. 13 - Prob. 4CTCh. 13 - Prob. 5CTCh. 13 - Prob. 6CTCh. 13 - Prob. 7CTCh. 13 - Prob. 8CTCh. 13 - Prob. 9CTCh. 13 - Prob. 10CTCh. 13 - Prob. 11CTCh. 13 - Prob. 12CTCh. 13 - Prob. 13CTCh. 13 - Prob. 14CTCh. 13 - Prob. 15CTCh. 13 - Prob. 16CTCh. 13 - Prob. 17CTCh. 13 - Prob. 18CTCh. 13 - Prob. 19CTCh. 13 - Prob. 20CTCh. 13 - Prob. 21CTCh. 13 - Prob. 1CURCh. 13 - Prob. 2CURCh. 13 - Prob. 3CURCh. 13 - Prob. 4CURCh. 13 - Prob. 5CURCh. 13 - Prob. 6CURCh. 13 - Prob. 7CURCh. 13 - Prob. 8CURCh. 13 - Prob. 9CURCh. 13 - Prob. 10CURCh. 13 - Prob. 11CURCh. 13 - Prob. 12CURCh. 13 - Prob. 13CURCh. 13 - Prob. 14CURCh. 13 - Prob. 15CURCh. 13 - Prob. 16CURCh. 13 - Prob. 17CUR
Additional Math Textbook Solutions
Find more solutions based on key concepts
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
Sampling Method. In Exercises 9-12, determine whether the sampling method appears to be sound or is flawed.
9. ...
Elementary Statistics
In Exercises 5–12, find and sketch the domain for each function.
7.
University Calculus: Early Transcendentals (4th Edition)
CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...
Thinking Mathematically (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Door 87.5in to 47 living 44.75 Closet 96in Window ISS.Sin 48in Train Table 96in 48in 132:2 Windowarrow_forward39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forwardA parallelogram with an area of 211.41 m^2 hast a base Thatcher measures 24.3m. Find ist height.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License