Vector Mechanics For Engineers
12th Edition
ISBN: 9781259977305
Author: BEER, Ferdinand P. (ferdinand Pierre), Johnston, E. Russell (elwood Russell), Cornwell, Phillip J., SELF, Brian P.
Publisher: Mcgraw-hill Education,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 13.192RP
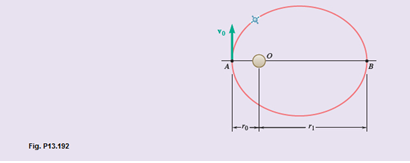
A satellite describes an elliptic orbit about a planet of mass M. The minimum and maximum values of the distance r from the satellite to the center of the planet are, respectively, r1 and r2. Use the principles of conservation of energy and conservation of angular momentum to derive the relation
where h is the angular momentum per unit mass of the satellite and G is the constant of gravitation.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
5. A 2-kg sphere is attached to a massless rigid rod attached to a fixed pivot point O. The rigid rod and
mass rotate in the horizontal plane. A moment is applied to the rod of magnitude M = 0.5t² N. m,
where t is in seconds. The length of the rod is 0.5 m. Determine the speed of the sphere after the
moment is applied for 5 seconds.
M(t)
A small 0.490-kg object moves on a frictionless horizontal table in a circular path of radius 2.50 m. The
angular speed is 3.83 rad/s. The object is attached to a string of negligible mass that passes through a small
hole in the table at the center of the circle. Someone under the table begins to pull the string downward to
make the circle smaller. If the string will tolerate a tension of no more than 123 N, what is the radius of the
smallest possible circle on which the object can move?
Number
Units
Blocks A and B have masses mA, and mB , respectively. Neglecting friction between all surfaces, draw the FBD and KD for each mass.
Chapter 13 Solutions
Vector Mechanics For Engineers
Ch. 13.1 - Block A is traveling with a speed v0 on a smooth...Ch. 13.1 - A 400-kg satellite is placed in a circular orbit...Ch. 13.1 - Prob. 13.2PCh. 13.1 - Prob. 13.3PCh. 13.1 - A 500-kg communications satellite is in a circular...Ch. 13.1 - Prob. 13.5PCh. 13.1 - Prob. 13.6PCh. 13.1 - Prob. 13.7PCh. 13.1 - A 2000-kg automobile starts from rest at point A...Ch. 13.1 - An athlete is holding 30 lb of weights at a height...
Ch. 13.1 - A 1.4-kg model rocket is launched vertically from...Ch. 13.1 - Packages are thrown down an incline at A with a...Ch. 13.1 - A package is thrown down an incline at A with a...Ch. 13.1 - Boxes are transported by a conveyor belt with a...Ch. 13.1 - Boxes are transported by a conveyor belt with a...Ch. 13.1 - A 1200-kg trailer is hitched to a 1400-kg car. The...Ch. 13.1 - A trailer truck enters a 2 percent uphill grade...Ch. 13.1 - The subway train shown is traveling at a speed of...Ch. 13.1 - The subway train shown is travelling at a speed of...Ch. 13.1 - Prob. 13.19PCh. 13.1 - The system shown is at rest when a constant 30-lb...Ch. 13.1 - Car B is towing car A at a constant speed of 10...Ch. 13.1 - The motor applies a constant downward force F=1050...Ch. 13.1 - The motor applies a constant downward force F to...Ch. 13.1 - Two blocks A and B, of mass 4 kg and 5 kg....Ch. 13.1 - Four 15-kg packages are placed as shown on a...Ch. 13.1 - A 3-kg block rests on top of a 2-kg block...Ch. 13.1 - Solve Prob. 13.26. assuming that the 2-kg block is...Ch. 13.1 - People with mobility impairments can gain great...Ch. 13.1 - A 7.5-lb collar is released from rest in the...Ch. 13.1 - A 10-kg block is attached to spring A and...Ch. 13.1 - A 5-kg collar A is at rest on top of, but not...Ch. 13.1 - A 0.75-lb brass (nonmagnetic) block A and a 0.5-lb...Ch. 13.1 - An uncontrolled automobile travelling at 65 mph...Ch. 13.1 - Two types of energy-absorbing fenders designed to...Ch. 13.1 - Nonlinear springs are classified as hard or soft,...Ch. 13.1 - A meteor starts from rest at a very great distance...Ch. 13.1 - Express the acceleration of gravity gh, at an...Ch. 13.1 - Prob. 13.38PCh. 13.1 - The sphere at A is given a downward velocity v0 of...Ch. 13.1 - The sphere at Ais given a downward velocity v0and...Ch. 13.1 - A bag is gently pushed off the top of a wall at A...Ch. 13.1 - A roller coaster starts from rest at A, rolls down...Ch. 13.1 - In Prob. 13.42. determine the range of values of h...Ch. 13.1 - A small block slides at a speed v on a horizontal...Ch. 13.1 - A small block slides at a speed v=8 ft/s on a...Ch. 13.1 - A chairlift is designed to transport 1000 skiers...Ch. 13.1 - Prob. 13.47PCh. 13.1 - The velocity of the lift of Prob. 13.47 increases...Ch. 13.1 - (a) A 120-lb woman rides a 15-lb bicycle up a...Ch. 13.1 - Prob. 13.50PCh. 13.1 - Prob. 13.51PCh. 13.1 - Prob. 13.52PCh. 13.1 - Prob. 13.53PCh. 13.1 - The elevator E has a weight of 6600 lb when fully...Ch. 13.2 - Two small balls A and B with masses 2m and m,...Ch. 13.2 - A small blocks is released from rest and slides...Ch. 13.2 - Prob. 13.55PCh. 13.2 - A loaded railroad car of mass m is rolling at a...Ch. 13.2 - A 750-g collar can slide along the horizontal rod...Ch. 13.2 - A 2-lb collar C may slide without friction along a...Ch. 13.2 - Solve Prob. 13.58 assuming the spring CD has been...Ch. 13.2 - A 500-g collar can slide without friction on the...Ch. 13.2 - For the adapted shuffleboard device in Prob 13.28....Ch. 13.2 - An elastic cable is to be designed for bungee...Ch. 13.2 - Prob. 13.63PCh. 13.2 - Prob. 13.64PCh. 13.2 - Prob. 13.65PCh. 13.2 - A thin circular rod is supported in a vertical...Ch. 13.2 - Prob. 13.67PCh. 13.2 - A spring is used to stop a 50-kg package that is...Ch. 13.2 - Solve Prob. 13.68 assuming the coefficient of...Ch. 13.2 - Prob. 13.70PCh. 13.2 - A roller coaster starts from rest at A, rolls down...Ch. 13.2 - Prob. 13.72PCh. 13.2 - A 10-lb collar is attached to a spring and slides...Ch. 13.2 - An 8-oz package is projected upward with a...Ch. 13.2 - If the package of Prob. 13.74 is not to hit the...Ch. 13.2 - A small package of weight W is projected into a...Ch. 13.2 - Prob. 13.77PCh. 13.2 - Prob. 13.78PCh. 13.2 - Prob. 13.79PCh. 13.2 - Prob. 13.80PCh. 13.2 - A force F acts on a particle P(x, y) which moves...Ch. 13.2 - Prob. 13.82PCh. 13.2 - Prob. 13.83PCh. 13.2 - Prob. 13.84PCh. 13.2 - (a) Determine the kinetic energy per unit mass...Ch. 13.2 - Prob. 13.86PCh. 13.2 - Prob. 13.87PCh. 13.2 - How much energy per pound should be imparted to a...Ch. 13.2 - Knowing that the velocity of an experimental space...Ch. 13.2 - Prob. 13.90PCh. 13.2 - Prob. 13.91PCh. 13.2 - Prob. 13.92PCh. 13.2 - Prob. 13.93PCh. 13.2 - Prob. 13.94PCh. 13.2 - Prob. 13.95PCh. 13.2 - Prob. 13.96PCh. 13.2 - Prob. 13.97PCh. 13.2 - Prob. 13.98PCh. 13.2 - Prob. 13.99PCh. 13.2 - Prob. 13.100PCh. 13.2 - Prob. 13.101PCh. 13.2 - Prob. 13.102PCh. 13.2 - Prob. 13.103PCh. 13.2 - Prob. 13.104PCh. 13.2 - Prob. 13.105PCh. 13.2 - Prob. 13.106PCh. 13.2 - Prob. 13.107PCh. 13.2 - Prob. 13.108PCh. 13.2 - Prob. 13.109PCh. 13.2 - Prob. 13.110PCh. 13.2 - Prob. 13.111PCh. 13.2 - Prob. 13.112PCh. 13.2 - Prob. 13.113PCh. 13.2 - Prob. 13.114PCh. 13.2 - Prob. 13.115PCh. 13.2 - A spacecraft of mass mdescribes a circular orbit...Ch. 13.2 - Prob. 13.117PCh. 13.2 - Prob. 13.118PCh. 13.3 - A large insect impacts the front windshield of a...Ch. 13.3 - The expected damages associated with two types of...Ch. 13.3 - The initial velocity of the block in position A is...Ch. 13.3 - Prob. 13.F2PCh. 13.3 - Prob. 13.F3PCh. 13.3 - Car A was traveling west at a speed of 15 m/s and...Ch. 13.3 - Prob. 13.F5PCh. 13.3 - A 35.000-Mg ocean liner has an initial velocity of...Ch. 13.3 - Prob. 13.120PCh. 13.3 - A sailboat weighing 980 lb with its occupants is...Ch. 13.3 - A truck is hauling a 300-kg log out of a ditch...Ch. 13.3 - The coefficients of friction between the load and...Ch. 13.3 - Steep safety ramps are built beside mountain...Ch. 13.3 - Baggage on the floor of the baggage car of a...Ch. 13.3 - Prob. 13.126PCh. 13.3 - Prob. 13.127PCh. 13.3 - Prob. 13.128PCh. 13.3 - Prob. 13.129PCh. 13.3 - Prob. 13.130PCh. 13.3 - Prob. 13.131PCh. 13.3 - The motor applies a constant downward force F=550...Ch. 13.3 - Prob. 13.133PCh. 13.3 - Prob. 13.134PCh. 13.3 - A 60-g model rocket is fired vertically. The...Ch. 13.3 - Prob. 13.136PCh. 13.3 - A crash test is performed between an SUV A and a...Ch. 13.3 - Prob. 13.138PCh. 13.3 - Prob. 13.139PCh. 13.3 - A 1.6 2-oz golf ball is hit with a golf club and...Ch. 13.3 - The triple jump is a track-and-field event in...Ch. 13.3 - Prob. 13.142PCh. 13.3 - Prob. 13.143PCh. 13.3 - A 28-g steel-jacketed bullet is fired with a...Ch. 13.3 - A 120-ton tugboat is moving at 6 ft/s with a slack...Ch. 13.3 - At an intersection, car B was traveling south and...Ch. 13.3 - The 650-kg hammer of a drop-hammer pile driver...Ch. 13.3 - Prob. 13.148PCh. 13.3 - Prob. 13.149PCh. 13.3 - Prob. 13.150PCh. 13.3 - Prob. 13.151PCh. 13.3 - Prob. 13.152PCh. 13.3 - Prob. 13.153PCh. 13.3 - In order to test the resistance of a chain to...Ch. 13.4 - A 5 -kg ball A strikes a 1-kg ball B that is...Ch. 13.4 - F6 A sphere with a speed v0 rebounds after...Ch. 13.4 - An 80-Mg railroad engine A coasting at 6.5 km/h...Ch. 13.4 - Prob. 13.F8PCh. 13.4 - Prob. 13.F9PCh. 13.4 - Block A of mass mA strikes ball B of mass mB with...Ch. 13.4 - Two steel blocks slide without friction on a...Ch. 13.4 - Prob. 13.156PCh. 13.4 - One of the requirements for tennis balls to be...Ch. 13.4 - Prob. 13.158PCh. 13.4 - Prob. 13.159PCh. 13.4 - Packages in an automobile parts supply house are...Ch. 13.4 - Prob. 13.161PCh. 13.4 - Prob. 13.162PCh. 13.4 - Prob. 13.163PCh. 13.4 - Two identical billiard balls can move freely on a...Ch. 13.4 - Two identical 40-lb curling stones have diameters...Ch. 13.4 - A 600-g ball A is moving with a velocity of...Ch. 13.4 - Two identical hockey pucks are moving on a hockey...Ch. 13.4 - Prob. 13.168PCh. 13.4 - Prob. 13.169PCh. 13.4 - The Mars Pathfinder spacecraft used large airbags...Ch. 13.4 - A girl throws a ball at an inclined wall from a...Ch. 13.4 - Rockfalls can cause major damage to roads and...Ch. 13.4 - Prob. 13.173PCh. 13.4 - cars of the same mass run head-on into each other...Ch. 13.4 - Prob. 13.175PCh. 13.4 - Prob. 13.176PCh. 13.4 - After having been pushed by an airline employee,...Ch. 13.4 - Blocks A and B each weigh 0.8 lb and block C...Ch. 13.4 - A 5-kg sphere is dropped from a height of y=2 m to...Ch. 13.4 - Prob. 13.180PCh. 13.4 - Prob. 13.181PCh. 13.4 - Block A is released from rest and slides down the...Ch. 13.4 - Prob. 13.183PCh. 13.4 - A test machine that kicks soccer balls has a 5-lb...Ch. 13.4 - Prob. 13.185PCh. 13.4 - Prob. 13.186PCh. 13.4 - A 2-kg sphere moving to the right with a velocity...Ch. 13.4 - When the rope is at an angle of a=30 , the 1-Ib...Ch. 13.4 - Prob. 13.189PCh. 13 - 34,000-Ib airplane lands on an aircraft carrier...Ch. 13 - Prob. 13.191RPCh. 13 - A satellite describes an elliptic orbit about a...Ch. 13 - Prob. 13.193RPCh. 13 - Prob. 13.194RPCh. 13 - A 300-g block is released from rest after a spring...Ch. 13 - A kicking-simulation attachment goes on the front...Ch. 13 - Prob. 13.197RPCh. 13 - Prob. 13.198RPCh. 13 - Prob. 13.199RPCh. 13 - Prob. 13.200RPCh. 13 - The 2-Ib ball at A is suspended by an inextensible...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- To understand how the conservation of energy and Newton's second law can be combined to solve kinetic problems. As shown, a large globe has a radius R and a frictionless surface. A small block with mass m starts sliding from rest at the top of the globe and slides along the globe’s surface. The block leaves the globe’s surface when it reaches a height hl above the ground. The system’s geometry is shown for an arbitrary height h. (Figure 1) Note that the subscripts used in this problem is the letter l and not the number 1. Consider what happens when the block leaves the globe’s surface. Which of the following statement or statements are correct? The net acceleration of the block is directed straight down. The component of the force of gravity toward the globe’s center is equal to the normal force’s magnitude. The force of gravity is the only force acting on the block.Consider what happens when the block leaves the globe’s surface. Which of the following statement or statements are…arrow_forwardA W disk = 5 lb disk is travelling around in a circle of radius ₁ with an initial tangential velocity of (UB)₁. The cord is pulled down through the hole at a constant velocity of ur. After a few seconds, the disk has a final speed of Vf. Neglect friction and the size of the ball. F|VI| T2 = t= UT B (VB)₁ T1 MB Values for the figure are given in the following table. Note the figure may not be to scale. Variable Value ft 15 (VB)₁ 5 r₁ ft S 2.5 ft ft S 4.5 12 S Vr a. Determine the tangential component of the velocity of the disk when it reaches its final speed, (V₂)+ b. Determine the radius of the rope from the disk to the hole when the disk reaches its final speed, 12. c. Determine the time required for the disk to reach its final speed, t. Round your final answers to 3 significant digits/figures. ft (V₂)t = S S A ftarrow_forwardA particle of momentum P1 collides with a particle at rest. After the collision, the particle initially at rest decays into two particles of momentum P3 and P4, respectively, while particle 1 continues in a straight line with momentum P1'. Knowing the magnitudes of all the momentum listed above and knowing that energy was not conserved during the process, find the angle θ (theta) between particles 3 and 4.arrow_forward
- Two blocks 1 and 2 are connected by a rope over a pulley as shown. The pulley is very light (massless) and rotates with essentially no friction. Calculate the mass of block 1, m1, given that the mass of block 2 is m2=5.5 kg and that block 2 moves and accelerates downwards at 3.57 m/s2 when θ=35∘ and μk=0.4. I think that I need to be using Newtons second law but I just dont know how to solve this. Can you please help?arrow_forwardA 300-mm cantilever beam BC with uniform cross section A-A is supporting an inclined 225-N force acting on the top of the beam at C as shown below. Y B A4 A+ 225 N 300 mm 3 X 10 mm 30 mm 10 mm Section A-A 2← y -10 mm 30 mm (a) Show that the second moment of area about the neutral axis of the cross section A-A is given by I = 267 500 mm 4. (b) Draw and label the normal-force, shear-force and bending-moment diagrams for the beam by analysing an appropriate free-body diagram. (c) Determine the maximum magnitude and y location of the normal stress at B (x whether it is compressive or tensile. = 0). Statearrow_forwardA satellite used in a cellular telephone network has a mass of 2380 kg and is in a circular orbit at a height of 850 km above the surface of the earth. Part A What is the gravitational force Fgrav on the satellite? Take the gravitational constant to be G = 6.67x10-11 N-m2/kg2, the mass of the earth to be me = 5.97x1024 kg, and the radius of the Earth to be re = 6.38×106 marrow_forward
- Three different objects, all with different masses, are initially at rest at the bottom of a set of steps. Each step is of uniform height d. The mass of each object is a multiple of the base mass m: object1 has mass 4.00m, object 2 has mass 1.96m, and object 3 has mass m. When the objects are at the bottom of the steps, define the total gravitational potential energy of the three-object system to be zero. If the objects are then relocated as shown, what is the new total potential energy of the system? Each answer requires the numerical coefficient to an 2 algebraic expression. Each algebraic expression is given using some combination of the variables m, g, and d, where g is the acceleration due to gravity. Enter only the numerical coefficient. (Example: If the answer is 1.23mgd, just enter 1.23)arrow_forward3) A small block of mass m slides frictionlessly in the given orbit. Calculate the magnitude of the resultant force acting on the block released at point A when it reaches point C. (g= 10 m/s², m= 1 kg) 76.48 N 30.41 N 60.83 N 91.25 N 3/10 50.99 N MONSTER h-4R D 10 pu CT Rarrow_forwardPravinbhaiarrow_forward
- Figure 2 G 0.75 m 2 m 1.5 m Figure 2 shows a 2000 kg lorry with a center of mass at G. Starting from rest, the lorry achieves a speed of 15 m/s under a constant acceleration after it has traveled 100 m. The front wheels are free to roll. Q8. What is the normal force of the wheels at A and B? (↑) (A) NA = 10.7 kN (B) NẠ=8.89 kN (C) NA= 8.89 kN (D) NA=10.7 kN Ng = 8,89 kN Ng = 10.7 kN Ng = 8,89 kN Ng = 10.7 kN Q11. Eccentric impact occurs when the line connecting the mass centers of the two bodies with the line of impact. (A) coincide (В) does not coincide (С) is parallel (D) is perpendicular Q12. Which of the following is not a conservative force? (A) Gravitational force (B) Elastic force (C) Frictional force (D) None of the abovearrow_forwardCan you please help me just with D, F,G harrow_forwardTwo objects with masses of 2.55 kg and 4.15 kg are connected by a light string that passes over a light frictionless pulley to form an Atwood machine. (a) Determine the tension in the string. (b) Determine the acceleration of each object. (c) Determine the distance each object will move in the first second of motion if they start from rest.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Introduction to Kinematics; Author: LearnChemE;https://www.youtube.com/watch?v=bV0XPz-mg2s;License: Standard youtube license