
a.
To find: The pyramid is regular with rectangular dimensions as 40 and 30.
a.
Answer to Problem 3PSA
The pyramid is not regular because all the lateral faces are not equal.
Explanation of Solution
Given information:
A pyramid has rectangular base with dimensions as 40 and 30.
Formula used:
The below theorem is used:
Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.

In right
Area of triangle:
b = base of triangle
h = height of triangle
Calculation:
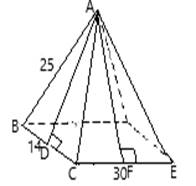
Draw altitude perpendicular to base.
The altitude AD can be calculated by applying Pythagoras Theorem.
In right angle triangle ABC , we get
The altitude AD drawn perpendicular divides the triangle face into two right
Lateral face is triangle.
Area of lateral face 1
Area of lateral face 1
In right angle triangle AFE , we get
The altitude AF drawn perpendicular divides the triangle face into two right triangles of
Lateral face is triangle.
Area of lateral face 2
Area of lateral face 2
Area of lateral face 1
The pyramid is not regular because all the lateral faces are not equal.
b.
To calculate: The lateral area of pyramid with rectangular dimensions as 40 and 30.
b.
Answer to Problem 3PSA
The lateral area of pyramid is
Explanation of Solution
Given information:
A pyramid has rectangular base with dimensions as 40 and 30.
Formula used:
The below theorem is used:
Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.
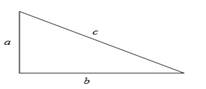
In right angle triangle,
Area of triangle:
b = base of triangle
h = height of triangle
Calculation:
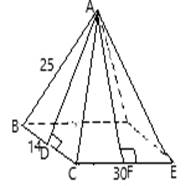
Draw altitude perpendicular to base.
The altitude AD can be calculated by applying Pythagoras Theorem.
In right angle triangle ABC , we get
The altitude AD drawn perpendicular divides the triangle face into two right triangles of
Lateral face is triangle.
Area of lateral face 1
Area of lateral face 1
In right angle triangle AFE , we get
The altitude AF drawn perpendicular divides the triangle face into two right triangles of
Lateral face is triangle.
Area of lateral face 2
Area of lateral face 2
Lateral area of pyramid = (2
Lateral area of pyramid
Lateral area of pyramid
c.
To find: The total area of pyramid with rectangular dimensions as 40 and 30.
c.
Answer to Problem 3PSA
The total area of pyramid is
Explanation of Solution
Given information:
A pyramid has rectangular base with dimensions as 40 and 30.
Formula used:
The below theorem is used:
Pythagoras theorem states that “In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”.
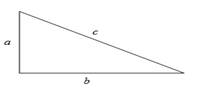
In right angle triangle,
Area of triangle:
b = base of triangle
h = height of triangle
Area of rectangle:
l = length of rectangle
w= width of rectangle Total Area = Lateral Area + Area of Rectangular Base
Calculation:
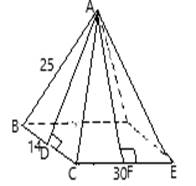
Draw altitude perpendicular to base.
The altitude can be calculated by applying Pythagoras Theorem.
In right angle triangle ABC , we get
The altitude AD drawn perpendicular divides the triangle face into two right triangles of
Lateral face is triangle.
Area of lateral face 1
Area of lateral face 1
In right angle triangle AFE , we get
The altitude AF drawn perpendicular divides the triangle face into two right triangles of
Lateral face is triangle.
Area of lateral face 2
Area of lateral face 2
Lateral area of pyramid = ( 2
Lateral area of pyramid
Lateral area of pyramid
Area of rectangular base
Area of rectangular base
Total Area = Lateral Area + Area of Rectangular Base
Total Area
Total Area
Chapter 12 Solutions
Geometry For Enjoyment And Challenge
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
College Algebra (7th Edition)
Elementary Statistics: Picturing the World (7th Edition)
University Calculus: Early Transcendentals (4th Edition)
- из Review the deck below and determine its total square footage (add its deck and backsplash square footage together to get the result). Type your answer in the entry box and click Submit. 126 1/2" 5" backsplash A 158" CL 79" B 26" Type your answer here.arrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardSelect all that apply. 104 8 6 4 2 U U' -10 -8 -6 4 -2 2 4 6 10 -2 V' W' -4 -6 -8 -10 W V Select 2 correct answerts! The side lengths are equal in measure. The scale factor is 1/5. The figure has been enlarged in size. The center of dilation is (0.0) 8 10 Xarrow_forward
- In the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardQll consider the problem -abu+bou+cu=f., u=0 ondor I prove atu, ul conts. @ if Blu,v) = (b. 14, U) + ((4,0) prove that B244) = ((c- — ob)4;4) ③if c±vbo prove that acuius v. elliptic.arrow_forwardQ3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)arrow_forward
- 7) In the diagram below of quadrilateral ABCD, E and F are points on AB and CD respectively, BE=DF, and AE = CF. Which conclusion can be proven? A 1) ED = FB 2) AB CD 3) ZA = ZC 4) ZAED/CFB E B D 0arrow_forward1) In parallelogram EFGH, diagonals EG and FH intersect at point I such that EI = 2x - 2 and EG = 3x + 11. Which of the following is the length of GH? a) 15 b) 28 c) 32 d) 56arrow_forward5) Which of the following are properties of all squares: 1. Congruent diagonals 2. Perpendicular diagonals 3. Diagonals that bisect vertex angles a) 1 and 2 only b) 1 and 3 only c) 2 and 3 only d) 1, 2, and 3arrow_forward
- 6) In an isosceles trapezoid HIJK it is known that IJ || KH. Which of the following must also be true? a) IJ = KH b) HIJK c) HIJK d) IJ KHarrow_forward4) When rectangle JKLM is plotted in the coordinate plane side JK has a slope equal to 3. What must be the slope of side MJ? a) 3/3 b) e 35 53 32 d) - 5arrow_forwardSolve for xarrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

