91st Edition

ISBN: 9780866099653

Author: Richard Rhoad, George Milauskas, Robert Whipple

Publisher: McDougal Littell

Videos

Question

Polygon with three sides, three angles, and three vertices. Based on the properties of each side, the types of triangles are scalene (triangle with three three different lengths and three different angles), isosceles (angle with two equal sides and two equal angles), and equilateral (three equal sides and three angles of 60°). The types of angles are acute (less than 90°); obtuse (greater than 90°); and right (90°).

Chapter 12, Problem 32CR

To determine

To find: The radius of the drainpipe when the water in it is 18 cm deep and the width of the surface of water is 48 cm.

Expert Solution & Answer

Answer to Problem 32CR

The radius of the drainpipe is 25 cm.

Explanation of Solution

Given Information:

Depth of the water = 18 cm

Width of the surface of water = 48 cm

Formula used:

By Pythagoras theorem,

$Hypotenuse2=Base2+Altitude2$

Calculation:

Let $x$ be the radius of the pipe.

Draw radius $OP$ and then draw a line $⊥$ the surface of the water and extend it to meet the circle.

We know that, a perpendicular from the centre of a circle to the chord bisect it.

So, $PR=482=24 cm$

Now, $OR⊥PR$

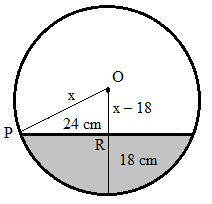
Geometry For Enjoyment And Challenge, Chapter 12, Problem 32CR

Here, $ΔORP$ forms a right triangle with $∠ORP=90o$

By Pythagoras theorem,

$Hypotenuse2=Base2+Altitude2$

$∴OP2=PR2+OR2∴x2=242+(x−18)2∴x2=576+x2−36x+324∴36x=900∴x=25 cm$

Hence, radius of the pipe is 25 cm.

Chapter 12, Problem 31CR

Chapter 12, Problem 33CR

Chapter 12 Solutions

Geometry For Enjoyment And Challenge

Ch. 12.1 - Prob. 1PSA Ch. 12.1 - Prob. 2PSA Ch. 12.1 - Prob. 3PSA Ch. 12.1 - Prob. 4PSA Ch. 12.1 - Prob. 5PSA Ch. 12.1 - Prob. 6PSB Ch. 12.1 - Prob. 7PSB Ch. 12.1 - Prob. 8PSB Ch. 12.1 - Prob. 9PSC Ch. 12.1 - Prob. 10PSC

Ch. 12.1 - Prob. 11PSC Ch. 12.2 - Prob. 1PSA Ch. 12.2 - Prob. 2PSA Ch. 12.2 - Prob. 3PSA Ch. 12.2 - Prob. 4PSA Ch. 12.2 - Prob. 5PSA Ch. 12.2 - Prob. 6PSB Ch. 12.2 - Prob. 7PSB Ch. 12.2 - Prob. 8PSB Ch. 12.2 - Prob. 9PSB Ch. 12.2 - Prob. 10PSC Ch. 12.2 - Prob. 11PSC Ch. 12.2 - Prob. 12PSC Ch. 12.2 - Prob. 13PSC Ch. 12.3 - Prob. 1PSA Ch. 12.3 - Prob. 2PSA Ch. 12.3 - Prob. 3PSA Ch. 12.3 - Prob. 4PSA Ch. 12.3 - Prob. 5PSA Ch. 12.3 - Prob. 6PSB Ch. 12.3 - Prob. 7PSB Ch. 12.3 - Prob. 8PSB Ch. 12.3 - Prob. 9PSB Ch. 12.3 - Prob. 10PSB Ch. 12.3 - Prob. 11PSB Ch. 12.3 - Prob. 12PSC Ch. 12.3 - Prob. 13PSC Ch. 12.3 - Prob. 14PSC Ch. 12.4 - Prob. 1PSA Ch. 12.4 - Prob. 2PSA Ch. 12.4 - Prob. 3PSA Ch. 12.4 - Prob. 4PSA Ch. 12.4 - Prob. 5PSA Ch. 12.4 - Prob. 6PSA Ch. 12.4 - Prob. 7PSB Ch. 12.4 - Prob. 8PSB Ch. 12.4 - Prob. 9PSB Ch. 12.4 - Prob. 10PSB Ch. 12.4 - Prob. 11PSB Ch. 12.4 - Prob. 12PSB Ch. 12.4 - Prob. 13PSB Ch. 12.4 - Prob. 14PSB Ch. 12.4 - Prob. 15PSB Ch. 12.4 - Prob. 16PSB Ch. 12.4 - Prob. 17PSB Ch. 12.4 - Prob. 18PSB Ch. 12.4 - Prob. 19PSC Ch. 12.4 - Prob. 20PSC Ch. 12.4 - Prob. 21PSC Ch. 12.4 - Prob. 22PSC Ch. 12.5 - Prob. 1PSA Ch. 12.5 - Prob. 2PSA Ch. 12.5 - Prob. 3PSA Ch. 12.5 - Prob. 4PSA Ch. 12.5 - Prob. 5PSA Ch. 12.5 - Prob. 6PSA Ch. 12.5 - Prob. 7PSA Ch. 12.5 - Prob. 8PSB Ch. 12.5 - Prob. 9PSB Ch. 12.5 - Prob. 10PSB Ch. 12.5 - Prob. 11PSB Ch. 12.5 - Prob. 12PSB Ch. 12.5 - Prob. 13PSB Ch. 12.5 - Prob. 14PSB Ch. 12.5 - Prob. 15PSB Ch. 12.5 - Prob. 16PSB Ch. 12.5 - Prob. 17PSC Ch. 12.5 - Prob. 18PSC Ch. 12.5 - Prob. 19PSC Ch. 12.5 - Prob. 20PSC Ch. 12.6 - Prob. 1PSA Ch. 12.6 - Prob. 2PSA Ch. 12.6 - Prob. 3PSA Ch. 12.6 - Prob. 4PSA Ch. 12.6 - Prob. 5PSA Ch. 12.6 - Prob. 6PSB Ch. 12.6 - Prob. 7PSB Ch. 12.6 - Prob. 8PSB Ch. 12.6 - Prob. 9PSB Ch. 12.6 - Prob. 10PSB Ch. 12.6 - Prob. 11PSB Ch. 12.6 - Prob. 12PSC Ch. 12.6 - Prob. 13PSC Ch. 12.6 - Prob. 14PSC Ch. 12.6 - Prob. 15PSC Ch. 12.6 - Prob. 16PSC Ch. 12.6 - Prob. 17PSD Ch. 12.6 - Prob. 18PSD Ch. 12 - Prob. 1RP Ch. 12 - Prob. 2RP Ch. 12 - Prob. 3RP Ch. 12 - Prob. 4RP Ch. 12 - Prob. 5RP Ch. 12 - Prob. 6RP Ch. 12 - Prob. 7RP Ch. 12 - Prob. 8RP Ch. 12 - Prob. 9RP Ch. 12 - Prob. 10RP Ch. 12 - Prob. 11RP Ch. 12 - Prob. 12RP Ch. 12 - Prob. 13RP Ch. 12 - Prob. 14RP Ch. 12 - Prob. 15RP Ch. 12 - Prob. 16RP Ch. 12 - Prob. 17RP Ch. 12 - Prob. 18RP Ch. 12 - Prob. 19RP Ch. 12 - Prob. 20RP Ch. 12 - Prob. 21RP Ch. 12 - Prob. 22RP Ch. 12 - Prob. 1CR Ch. 12 - Prob. 2CR Ch. 12 - Prob. 3CR Ch. 12 - Prob. 4CR Ch. 12 - Prob. 5CR Ch. 12 - Prob. 6CR Ch. 12 - Prob. 7CR Ch. 12 - Prob. 8CR Ch. 12 - Prob. 9CR Ch. 12 - Prob. 10CR Ch. 12 - Prob. 11CR Ch. 12 - Prob. 12CR Ch. 12 - Prob. 13CR Ch. 12 - Prob. 14CR Ch. 12 - Prob. 15CR Ch. 12 - Prob. 16CR Ch. 12 - Prob. 17CR Ch. 12 - Prob. 18CR Ch. 12 - Prob. 19CR Ch. 12 - Prob. 20CR Ch. 12 - Prob. 21CR Ch. 12 - Prob. 22CR Ch. 12 - Prob. 23CR Ch. 12 - Prob. 24CR Ch. 12 - Prob. 25CR Ch. 12 - Prob. 26CR Ch. 12 - Prob. 27CR Ch. 12 - Prob. 28CR Ch. 12 - Prob. 29CR Ch. 12 - Prob. 30CR Ch. 12 - Prob. 31CR Ch. 12 - Prob. 32CR Ch. 12 - Prob. 33CR Ch. 12 - Prob. 34CR Ch. 12 - Prob. 35CR Ch. 12 - Prob. 36CR Ch. 12 - Prob. 37CR Ch. 12 - Prob. 38CR Ch. 12 - Prob. 39CR Ch. 12 - Prob. 40CR Ch. 12 - Prob. 41CR Ch. 12 - Prob. 42CR

Additional Math Textbook Solutions

Find more solutions based on key concepts

In Exercises 13–16, find the margin of error for the values of c, ?, and n. 13. c = 0.95, ? = 5.2, n = 30

Elementary Statistics: Picturing the World (7th Edition)

Differentiating and integrating power series Find the power series representation for g centered at 0 by differ...

Calculus: Early Transcendentals (2nd Edition)

The four flaws in the given survey.

Elementary Statistics

1. How many solutions are there to ax + b = 0 with ?

College Algebra with Modeling & Visualization (5th Edition)

Assessment 1-1A In a big red box, there are 7 smaller blue boxes. In each of the blue boxes, there are 7 black ...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

Choose one of the answers in each case. In statistical inference, measurements are made on a (sample or popula...

Introductory Statistics

Knowledge Booster

$Geometry$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.