Chapter 12.1, Problem 21PPS

(a)

To determine

To draw: the figureand complete the table.

Answer to Problem 21PPS

Name	Triangular Pyramid	Square Pyramid	Pentagonal Pyramid
Vertices	4	5	6
Faces	4	5	6
Edges	6	8	10

Explanation of Solution

Given:

Consider the table

Name	Triangular Pyramid	Square Pyramid	Pentagonal Pyramid
Vertices	4	5
Faces			6
Edges		8

Calculation:

The objective is to complete the table.

Take the triangular pyramid. The figure of a triangular pyramid is shown below.

  

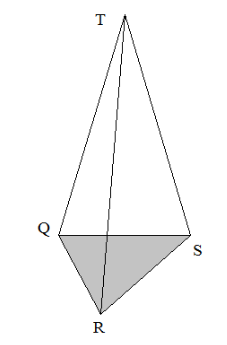
The faces of the triangular pyramid are $QRS,QTR,RTS,QTS$ .

The edges are the line where the faces intersect. The edges are $\overline{QT},\overline{QR},\overline{RS},\overline{TS},\overline{TR},\overline{QS}$ .

Therefore, the number of faces of the triangular pyramid is 4 and the number of edges of the triangular pyramid is 6.

Next, take the square pyramid. The figure of a square pyramid is shown below.

  

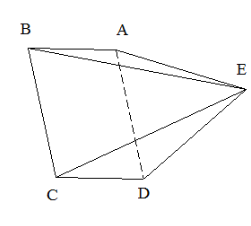
The faces of the square pyramid are $ABCD,AEB,BEC,CED,AED$ .

The edges are the line where the faces intersect. The edges are $\overline{AB},\overline{BC},\overline{CD},\overline{AD},\overline{AE},\overline{BE},\overline{CE},\overline{DE}$ .

Therefore, the number of faces of the square pyramid is 5 and the number of edges of the triangular pyramid is 8.

Lastly, take the pentagonal pyramid. The figure of a pentagonal pyramid is shown below.

  

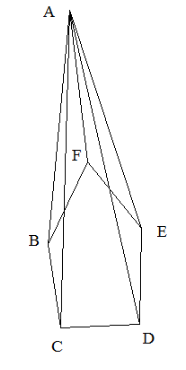
The vertices are $A,B,C,D,E,F$ .

The faces of the pentagonal pyramid are $BCDEF,AFB,AFE,AED,ACD,ABC$ .

The edges are the line where the faces intersect. The edges are $\overline{AB},\overline{AC},\overline{AD},\overline{AE},\overline{AF},\overline{BF},\overline{FE},\overline{DE},\overline{DC},\overline{BC}$ .

Therefore, the number of vertices of the pentagonal pyramid is 6, the number of faces of the pentagonal pyramid is 6 and the number of edges of the triangular pyramid is 10.

Conclusion:

Therefore, the complete table is

Name	Triangular Pyramid	Square Pyramid	Pentagonal Pyramid
Vertices	4	5	6
Faces	4	5	6
Edges	6	8	10

(b)

To determine

To explain:about the number of edges,vertices and faces.

Answer to Problem 21PPS

Here, $\text{No}\text{. Edges = No}\text{. of Vertices + No}\text{. of Faces – 2}\text{.}$

Explanation of Solution

The objective is to state the relation between the vertices, faces and the edges.

The faces and the number of vertices of a pyramid are always equal. The relation between vertices, faces and the edges is the number of edges is equal to the sum of the number of vertices and the number faces minus 2.

That is,

  $\text{No}\text{. Edges = No}\text{. of Vertices + No}\text{. of Faces – 2}\text{.}$

Conclusion:

Therefore, $\text{No}\text{. Edges = No}\text{. of Vertices + No}\text{. of Faces – 2}\text{.}$

(c)

To determine

To find: the equationcomparing vertices edges and faces

Answer to Problem 21PPS

The equation is $E=V+F-2$ .

Explanation of Solution

Calculation:

The objective is to write an equation that compares the sum of the number of vertices V and the number of faces F to the number of edges E.

The relation between edges, vertices and faces is

No. of Edges = No. of Vertices + No. of faces - 2

  $E=V+F-2$

Conclusion:

Therefore,the equation is $E=V+F-2$ .