
11.101 and 11.102 Each member of the truss shown is made of steel and has the cross-sectional area shown. Using E = 29 × 10 psi, determine the deflection indicated.
11.101 Vertical deflection of joint C.
11.102 Horizontal deflection of joint C.
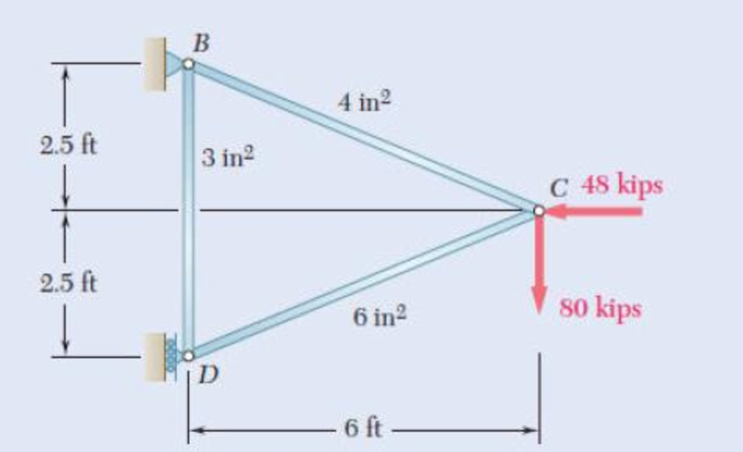
Fig. P11.101 and P11.102
Calculate the vertical deflection of joint C
Answer to Problem 101P
The vertical deflection of joint C
Explanation of Solution
Given information:
The Young’s modulus of the steel (E) is
The area of the member BC
The area of the member BD
The area of the member CD
The vertical load act at the joint C (P) is
The horizontal load act at the joint C (G) is
The length of the member BD
The length of the member (L) is
Calculation:
Show the free body diagram of the truss members as in Figure 1.
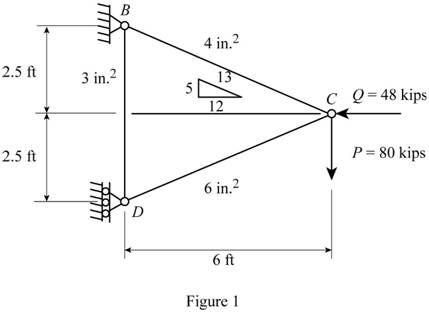
Refer to Figure 1.
The length of the member BC
The length of the member CD
The length of the member BD
Show the free body diagram of the joint C as in Figure 2.

Here,
Refer to Figure 2.
Calculate the horizontal forces by applying the equation of equilibrium:
Sum of horizontal forces is equal to 0.
Calculate the vertical forces by applying the equation of equilibrium:
Sum of vertical forces is equal to 0.
Calculate the force act at the member CD
Substitute
Calculate the force act at the member BC
Substitute
Show the diagram of the joint D as in Figure 3.
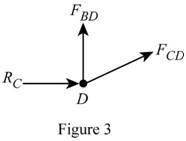
Here,
Refer to Figure 3.
Calculate the vertical forces by applying the equation of equilibrium:
Sum of vertical forces is equal to 0.
Substitute
Partial differentiate the force act at the member BC
Calculate the deflection of the member BC
Substitute
Partial differentiate the force act at the member CD
Calculate the deflection of the member CD
Substitute
Partial differentiate the force act at the member BD
Calculate the strain energy of the member BD
Substitute
Calculate the vertical deflection of joint C
Substitute
Substitute
Hence the vertical deflection of joint C
Want to see more full solutions like this?
Chapter 11 Solutions
EBK MECHANICS OF MATERIALS
- The rod ABC is made of an aluminum for which E = 71.15 GPa. Knowing that P=10.2 kN and Q=51.62kN, determine the deflection (in um) of point B y=0.46 and z=0.56. Round off the final answer in four decimal places.arrow_forwardQuestion 6* Each member of the truss shown is made of steel and has the cross-sectional area of 400mm². Use Castigliano's theorem to determine the vertical and horizontal deflections of joint A. P = 3 KN E = 200 GPa A VP m F 2.5 kN 1 m. E B -1 m. D 1 marrow_forwardThe rod ABC is made of an aluminum for which E = 71.86 GPa. Knowing that P = 7.72 kNand Q = 48.58 kN,determine the deflection (in μm) of point A if y = 0.48 and z = 0.59. Round off the final answer in three decimal places.arrow_forward
- 3.2 kN 300 mm B 75 mm A 9.77 The steel bars BE and AD each have a 6 × 18-mm cross section. Knowing that E = 200 GPa, determine the deflections of points A, B, and C of the rigid bar ABC. 400 mm-+400 mm Fig. P9.77arrow_forwardFbd ,formula and calculation should be included. Please work it fast without wasting a time. 1)The rod ABC is made of an aluminum for which E = 70 GPa. Knowing that P = 9 kN and Q = 14 kN, determine the deflection of: (a) Point A, (b) Point B. Consider upward to be positive.arrow_forward11.22 (B). Determine the vertical deflection of point A on the bent cantilever shown in Fig. 11.29 when loaded at A with a vertical load of 25 N. The cantilever is built in at B, and El may be taken as constant throughout and equal to 450 N m?. [B.P.] [0.98 mm.] B. 125 mm rad. -125mm A 25Narrow_forward
- Each of the links AB and CD is made of aluminum (E = 75GPa) and has a cross-section area if 125 mm2. Knowing that they support therigid member BC, determine the deflection of point E.arrow_forwardi need answer on this asap. thank you! Each of the links AB and CD is made of aluminum and has a cross-sectional area of 0.2 sq.in. Knowing that they support the rigid member BC, determine the downward deflection (in inches) of point B. if x = 13.7 in, y = 28.1 in, z = 20 in, E = 10754407 psi, and P = 26 kips. Round off the final answer to five decimal places.arrow_forwardEach of the AB and CD links are made of aluminum D (E = 10,900,000 psi) and have a cross-sectional area of 0.4 in 2. Knowing that they support RIGID element BC, determine the deflection of point E. 18 in. P= 1 kip E B - 22 in. 10 in.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





