
a.
To calculate:Thearea of
a.
Answer to Problem 1PSA
Thearea of triangle ABCis 6 .
Explanation of Solution
Given information:
In ΔABC
Side AB=3,
Side BC=4,
Side AC=5.
Formula used:
We can use Heron’s Formula to determine the area of a triangle when lengths of sides are given.
s=a+b+c2
a , b and c are sides of triangle
Area of triangle:
A=√s(s−a)(s−b)(s−c)
Calculation:
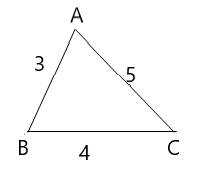
AB , BC and CA are sides of triangle ABC .
s=AB+BC+CA2=3+4+52=6
Area of triangle ABC :
A=√s(s−a)(s−b)(s−c)A=√6(6−3)(6−4)(6−5)A=√6×3×2×1A=√36A=6
b.
To find: The area of triangle DEF .
b.
Answer to Problem 1PSA
The area of triangle DEF is 2√5 .
Explanation of Solution
Given information:
In ΔDEF
Side DE=3,
Side EF=3,
Side DF=4.
Formula used:
We can use Heron’s Formula to determine the area of a triangle when lengths of sides are given.
s=a+b+c2
a , b and c are sides of triangle
Area of triangle:
A=√s(s−a)(s−b)(s−c)
Calculation:
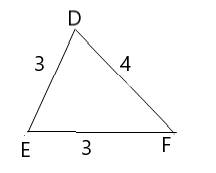
DE , EF and DF are sides of triangle DEF .
s=DE+EF+DF2=3+3+42=5
Area of triangle DEF :
A=√s(s−a)(s−b)(s−c)A=√5(5−3)(5−3)(5−4)A=√5×2×2×1A=√20A=2√5
c.
To find: The area of triangle LMN .
c.
Answer to Problem 1PSA
The area of triangle LMN is 10√2 .
Explanation of Solution
Given information:
In ΔLMN
Side LM=5,
Side MN=6,
Side LN=9.
Formula used:
We can use Heron’s Formula to determine the area of a triangle when lengths of sides are given.
s=a+b+c2
a , b and c are sides of triangle
Area of triangle:
A=√s(s−a)(s−b)(s−c)
Calculation:
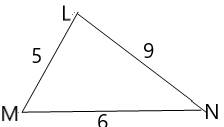
LM , MN and LN are sides of triangle LMN .
s=LM+MN+LN2=5+6+92=10
Area of triangle LMN :
A=√s(s−a)(s−b)(s−c)A=√10(10−5)(10−6)(10−9)A=√10×5×4×1A=√200A=10√2
d.
To find: The area of triangle OPQ .
d.
Answer to Problem 1PSA
The area of triangle OPQ is 6√3 .
Explanation of Solution
Given information:
In ΔOPQ
Side OP=3,
Side PQ=7,
Side OQ=8.
Formula used:
We can use Heron’s Formula to determine the area of a triangle when lengths of sides are given.
s=a+b+c2
a , b and c are sides of triangle
Area of triangle:
A=√s(s−a)(s−b)(s−c)
Calculation:
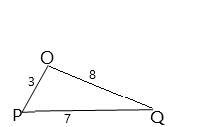
LM , MN and LN are sides of triangle LMN .
s=OP+PQ+OQ2=3+7+82=9
Area of triangle LMN :
A=√s(s−a)(s−b)(s−c)A=√9(9−3)(9−7)(9−8)A=√9×6×2×1A=√108A=6√3
e.
To find: The area of triangle XYZ .
e.
Answer to Problem 1PSA
The area of triangle XYZ is 60 .
Explanation of Solution
Given information:
In ΔXYZ
Side XY=8,
Side YZ=15,
Side XZ=17.
Formula used:
We can use Heron’s Formula to determine the area of a triangle when lengths of sides are given.
s=a+b+c2
a , b and c are sides of triangle
Area of triangle:
A=√s(s−a)(s−b)(s−c)
Calculation:
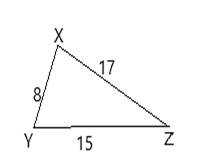
XY , YZ and XZ are sides of triangle XYZ .
s=XY+YZ+XZ2=8+15+172=20
Area of triangle XYZ :
A=√s(s−a)(s−b)(s−c)A=√20(20−8)(20−15)(20−17)A=√20×12×5×3A=√3600A=60
f.
To find: The area of triangle UVW .
f.
Answer to Problem 1PSA
The area of triangle UVW is 84 .
Explanation of Solution
Given information:
In ΔUVW
Side UV=13,
Side VW=14,
Side UW=15.
Formula used:
We can use Heron’s Formula to determine the area of a triangle when lengths of sides are given.
s=a+b+c2
a , b and c are sides of triangle
Area of triangle:
A=√s(s−a)(s−b)(s−c)
Calculation:
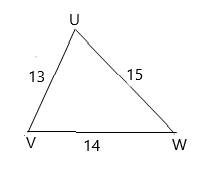
UV , VW and UW are sides of triangle UVW .
s=UV+VW+UW2=13+14+152=21
Area of triangle UVW :
A=√s(s−a)(s−b)(s−c)A=√21(21−13)(21−14)(21−15)A=√21×8×7×6A=√7056A=84
Chapter 11 Solutions
Geometry For Enjoyment And Challenge
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
College Algebra (7th Edition)
Elementary Statistics (13th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- Decomposition geometry: Mary is making a decorative yard space with dimensions as shaded in green (ΔOAB).Mary would like to cover the yard space with artificial turf (plastic grass-like rug). Mary reasoned that she could draw a rectangle around the figure so that the point O was at a vertex of the rectangle and that points A and B were on sides of the rectangle. Then she reasoned that the three smaller triangles resulting could be subtracted from the area of the rectangle. Mary determined that she would need 28 square meters of artificial turf to cover the green shaded yard space pictured exactly.arrow_forward7. 11 m 12.7 m 14 m S V=B₁+ B2(h) 9.5 m 16 m h+s 2 na 62-19 = 37 +, M h² = Bu-29arrow_forwardwhat would a of a interscribed angle be with an arc of 93 degrees and inside abgles of 111 and 98arrow_forward
- 6arrow_forwardDoor 87.5in to 47 living 44.75 Closet 96in Window ISS.Sin 48in Train Table 96in 48in 132:2 Windowarrow_forward39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

