
Concept explainers
During a parasailing ride, the boat is traveling at a constant 30 km/hr with a 200-m long tow line. At the instant shown, the angle between the line and the water is 30° and is increasing at a constant rate of 2°/s. Determine the velocity and acceleration of the parasailer at this instant.
Fig. P11.163 and P11.164

The velocity
Answer to Problem 11.163P
The velocity
Explanation of Solution
Given Information:
The boat is traveling at a constant speed
The radius (r) of tow line is
The angle
Calculation:
Convert the kilometer per hour to meter per second.
Consider
Show the Free body diagram of parasailer and boat as in Figure (1).
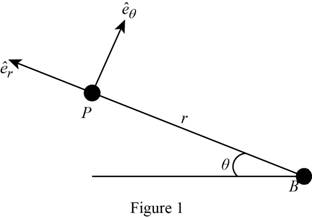
Write the velocity
The acceleration vector of the boat is as follows:
Differentiate angle
Differentiate radius (r) with respective to time (t).
Differentiate
Write the expression for velocity vector
Here,
Write the expression for acceleration vector
Here,
Calculate the velocity vector
Substitute 0 for
Calculate the acceleration vector
Substitute 0 for
Write the velocity vector
Substitute
Write the acceleration vector
Substitute
Calculate the velocity vector
Substitute
Here,
Calculate the velocity
Substitute
Calculate the angle
Substitute
Calculate the acceleration vector
Substitute
Here,
Calculate the acceleration
Substitute
Calculate the angle
Substitute
Therefore, the velocity
Want to see more full solutions like this?
Chapter 11 Solutions
VECTOR MECH...,STAT.+DYN.(LL)-W/ACCESS
- SAMPLE PROBLEM A motorist is traveling on a curved section of highway of radius 2500 ft at the speed of 60 mi/h. The motorist suddenly applies the brakes, causing the automobile to slow down at a constant rate. Knowing that after 8 s the speed has been reduced to 45 mi/h, determine the acceleration of the automobile immediately after the brakes have been applied. V= 60 mi /h 2500 ftarrow_forwardAn outdoor track is 420 ft in diameter. A runner increases her speed at a constant rate from 14 to 24 ft/s over a distance of 95 ft. Determine the magnitude of the total acceleration of the runner 2 s after she begins to increase her speed. Fig. P11.137arrow_forwardPROBLEM 11.46 Car A is parked along the northbound lane of a highway, and car B is traveling in the southbound lane at a constant speed of 60 mi/h. Att=0, A starts and accelerates at a constant rate a, while at t=5s, B begins to slow down with a constant deceleration of magnitude a 16. Knowing that when the cars pass each other x = 294 ft and v =VR, determine (a) the acceleration a, (b) when the vehicles pass each other, (c) the distance d between the vehicles at t=0. (-60 mi/h (l 0 Name - Mortada Ali SOLUTION Qassem VA =0+a,t Xg =0+(vg)ot (và)o =60 mi/h = 88 ft/s Xg = (88 ft/s)(5 s) = 440 ft 1 Va = ("g), + a»(t – 5) ag =--a, Assume t> 5 s when the cars pass each other. At that time (t AB ), VA = VB: astAB = (88 ft/s) – -(1 AB -5) 294 ft =ai. = 294 ft: a,(공AB-8)- 88 Then %3D 294 441B - 343t AB + 245 = 0 or Hey I want a nice handwriting please with my name the same solutionarrow_forward
- During a parasailing ride, the boat is traveling at a constant 38 km/hr with a 200-m long tow line. At the instant shown, the angle between the line and the water is 30º and is increasing at a constant rate of 2º/s. Determine the velocity and acceleration of the parasailer at this instant. The velocity of the parasailer is m/s ⦨ °. ? The acceleration of the parasailer is m/s2 ⦪ °. ? Note: please show step by step solution. Hence, double check the solution. For correction purposes!. I require handwritten working out please!. Kindly, please meticulously, check the image for conceptual understanding and for extra information purposes!. Also on occasions, I receive wrong answers!!. Please go through the question and working out step by step when you finish them. Appreciate your time!.arrow_forwardPlease solve with white paper and detailed solution thanks Q2/ PROBLEM 11.46 Car A is parked along the northbound lane of a highway, and car B is traveling in the southbound lane at a constant speed of 60 mi/h. At t 0, A starts and accelerates at a constant rate a,, while at t = 5 s, B begins to slow down with a constant deceleration of magnitude a /6. Knowing that when the cars pass each other x = 294 ft and v, = v, detemine (a) the acceleration a, (b) when the vehicles pass each other, (c) the distance d betwveen the vehicles at 1 = 0. (v= G0 mi/h (Da)g = 0 Barrow_forward11.10 The acceleration of a particle is directly proportional to the square of the time t. When 1 = 0, the particle is at r = 24 m. Knowing that at 1 = 6 s, r = 96 m and o = 18 m/s, express r and o in terms of 1. 11.11 The acceleration of a particle is directly proportional to the time t. At 1 = 0, the velocity of the particle is o = 16 in./s. Knowing that D = 15 in./s and that r = 20 in. when t = 1 s. determine the velocity, the position, and the total distance traveled when 1 = 7 s. 11.12 The acceleration of a particle is defined by the relation a = kt?. (a) Knowing that u = -32 ft/s when t = 0 and that o = +32 fU/s when t = 4 s, determine the constant k. (b) Write the equations of motion, knowing also that + = 0 when + = 4 s.arrow_forward
- Do not copy others' solution. Write legibly if handwritten.arrow_forwardCopyright © McGraw-Hill Education. Permission required for reproduction or display. The pitcher in a softball game throws a ball with an initial velocity vo of 108 km/h at an angle a with the horizontal. If the height of the ball at Point B is A В 0.6 m 0.68 m 0.68 m, determine (a) the angle a, (b) the angle O that the velocity of the ball at Point B forms with 14 m the horizontal.arrow_forwardA train is moving horizontally to the right with the speed of VT=60 mi/h. Meanwhile, a car is traveling toward the train with the speed of VC=30 mi/h and a 30deg angle with respect to horizontal direction. Select the correct expression of the velocity vector of the train relative to the car ___________mi/h A. (60-30cos30°)-30sin30° B. (60-30cos30°) +30sin30° C. (60+30cos30°)-30sin30° D. (30cos30°-60) +30sin30°arrow_forward
- RELATIVE MOTION Please show your neat and complete solution to this problem. ASAP! Thanks.arrow_forward11.53 A farmer lifts his hay bales into the top loft of his barn by walking his horse forward with a constant velocity of 1 ft/s. Determine the velocity and acceleration of the hay bale when the horse is 10 ft away from the barn. 20 ft Fig. P11.53arrow_forwardA Scotch yoke is a mechanism that transforms the circular motion of a crank into the reciprocating motion of a shaft (or vice versa). It has been used in a number of different internal combustion engines and in control valves. In the Scotch yoke shown, the acceleration of Point A is defined by the relation a=-1.5sin(kt) , where a and t are expressed in m/s2 and seconds, respectively, and k=3 rad/s. Knowing that x=0 and v=0.6 m/s when t =0, determine the position of Point A when t=0.5 s.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





