Chapter 11.3, Problem 18E

a.

To determine

Find the value of $b_1$.

Answer to Problem 18E

The slope $b_1$ is –0.063.

Explanation of Solution

Calculation:

The given information is that the sample data consists of 7 values for x and y.

Slope or $b_1$:

$b_1=r\frac{s_y}{s_x}$

where,

r represents the correlation coefficient between x and y.

$s_y$ represents the standard deviation of y.

$s_x$ represents the standard deviation of x.

Software procedure:

Step-by-step procedure to find the mean, standard deviation for x and y values using MINITAB is given below:

• • Choose Stat > Basic Statistics > Display Descriptive Statistics.
• • In Variables enter the columns of x and y.
• • Choose Options Statistics, and select Mean and Standard deviation.
• • Click OK.

Output obtained from MINITAB is given below:

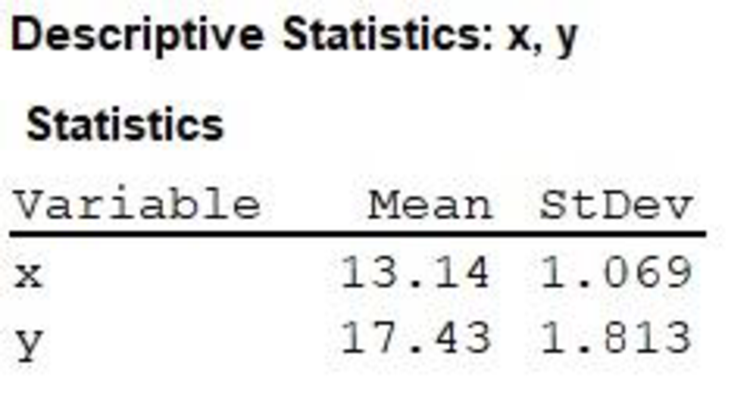
Correlation:

$r=\frac{1}{n-1}{\displaystyle \sum \left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)}$

The table shows the calculation of correlation:

x	y	$x-\overline{x}$	$y-\overline{y}$	$\frac{x-\overline{x}}{s_x}$	$\frac{y-\overline{y}}{s_y}$	$\left(\frac{x-\overline{x}}{s_x}\right)\left(\frac{y-\overline{y}}{s_y}\right)$
12	18	–1.14	0.57	–1.0664	0.3144	–0.3353
13	19	–0.14	1.57	–0.1310	0.86597	–0.1134
15	18	1.86	0.57	1.7399	0.3144	0.547
13	16	–0.14	–1.43	–0.1310	–0.7887	0.1033
12	16	–1.14	–1.43	–1.0664	–0.7887	0.8411
14	15	0.86	–2.43	0.8045	–1.3403	–1.0783
13	20	–0.14	2.57	–0.1310	1.41754	–0.1856
						–0.2212

Thus, the correlation is

$\begin{array}{c}r=\frac{-0.2212}{7-1}\\ =\frac{-0.2212}{6}\\ =-0.0369\end{array}$

$b_1=r\frac{s_y}{s_x}$

Substitute r as –0.0369, $s_y$ as 1.813 and $s_x$ as 1.069.

$\begin{array}{c}{b}_1=-0.0369\left(\frac{1.813}{1.069}\right)\\ =-0.0369\left(1.696\right)\\ =-0.063\end{array}$

Thus, the slope $b_1$ is –0.063.

b.

To determine

Find the residual standard deviation $s_e$.

Answer to Problem 18E

The residual standard deviation $s_e$ is 1.98.

Explanation of Solution

Calculation:

Finding the value of the intercept term before find the residual standard deviation:

Intercept or $b_0$:

$b_0=\overline{y}-b_1\overline{x}$

$\overline{y}$ represents the mean of y values.

$\overline{x}$ represents the mean of x values.

$b_1$ represents the slope coefficient.

Substitute $\overline{y}$ as 17.43, $\overline{x}$ as 13.14 and $b_1$ as 0.063.

$\begin{array}{c}{b}_0=17.43-\left(-0.063\right)\left(13.14\right)\\ =17.43+0.83\\ =18.26\end{array}$

Thus, the intercept $b_0$ is 18.26.

The residual standard deviation $s_e$ is calculated using the formula,

$s_e=\sqrt{\frac{{{\displaystyle \sum \left(y-\widehat{y}\right)}}^2}{n-2}}$

Where,

${{\displaystyle \sum \left(y-\widehat{y}\right)}}^2$ represents the sum of squares due to error

n represents the sample size.

Thus, the estimated regression equation is $\widehat{y}=18.260-0.063x$

Use the estimated regression equation to find the predicted value of y for each value of x.

x	y	$\widehat{y}$	$y-\widehat{y}$	${\left(y-\widehat{y}\right)}^2$
12	18	17.504	0.496	0.24602
13	19	17.441	1.559	2.43048
15	18	17.315	0.685	0.46922
13	16	17.441	-1.441	2.07648
12	16	17.504	-1.504	2.26202
14	15	17.378	-2.378	5.65488
13	20	17.441	2.559	6.54848
Total				19.6876

Substitute ${{\displaystyle \sum \left(y-\widehat{y}\right)}}^2$ as 19.6876 and n as 7.

$\begin{array}{c}{s}_e=\sqrt{\frac{19.6876}{7-2}}\\ =\sqrt{\frac{19.6876}{5}}\\ =\sqrt{3.938}\\ =1.98\end{array}$

Thus, the residual standard deviation $s_e$ is 1.98.

c.

To determine

Find the sum of squares for x.

Answer to Problem 18E

The sum of squares for x is 6.8572.

Explanation of Solution

Calculation:

The table shows the calculation of sum of squares for x

x	$x-\overline{x}$	${\left(x-\overline{x}\right)}^2$
12	–1.14	1.2996
13	–0.14	0.0196
15	1.86	3.4596
13	–0.14	0.0196
12	–1.14	1.2996
14	0.86	0.7396
13	–0.14	0.0196
Total		6.8572

Thus, the sum of squares for x is 6.8572.

d.

To determine

Find the standard error of $b_1,s_b$.

Answer to Problem 18E

The standard error of $b_1$$s_b$ is 0.756.

Explanation of Solution

Calculation:

The standard error of $b_1$ is calculated by using the formula:

$s_b=\frac{s_e}{\sqrt{{\displaystyle \sum {\left(x-\overline{x}\right)}^2}}}$

Where,

$s_e$ represents the residual standard deviation.

${\displaystyle \sum {\left(x-\overline{x}\right)}^2}$ represents the sum of squares due to x.

Substitute ${\displaystyle \sum {\left(x-\overline{x}\right)}^2}$ as 6.8572 and $s_e$ as 1.98.

$\begin{array}{c}{s}_b=\frac{1.98}{\sqrt{6.8572}}\\ =\frac{1.98}{2.619}\\ =0.756\end{array}$

Thus, the standard error of $b_1$, $s_b$ is 0.756.

e.

To determine

Find the critical value for a 95% confidence interval of ${\beta }_1$.

Answer to Problem 18E

The critical value for a 95% confidence interval of ${\beta }_1$ is 3.182.

Explanation of Solution

Calculation:

Critical value:

Software procedure:

Step-by-step procedure to find the critical value using MINITAB is given below:

• • Choose Graph > Probability Distribution Plot choose View Probability > OK.
• • From Distribution, choose ‘t’ distribution.
• • In Degrees of freedom, enter 5.
• • Click the Shaded Area tab.
• • Choose Probability and Two tail for the region of the curve to shade.
• • Enter the Probability value as 0.05.
• • Click OK.

Output obtained from MINITAB is given below:

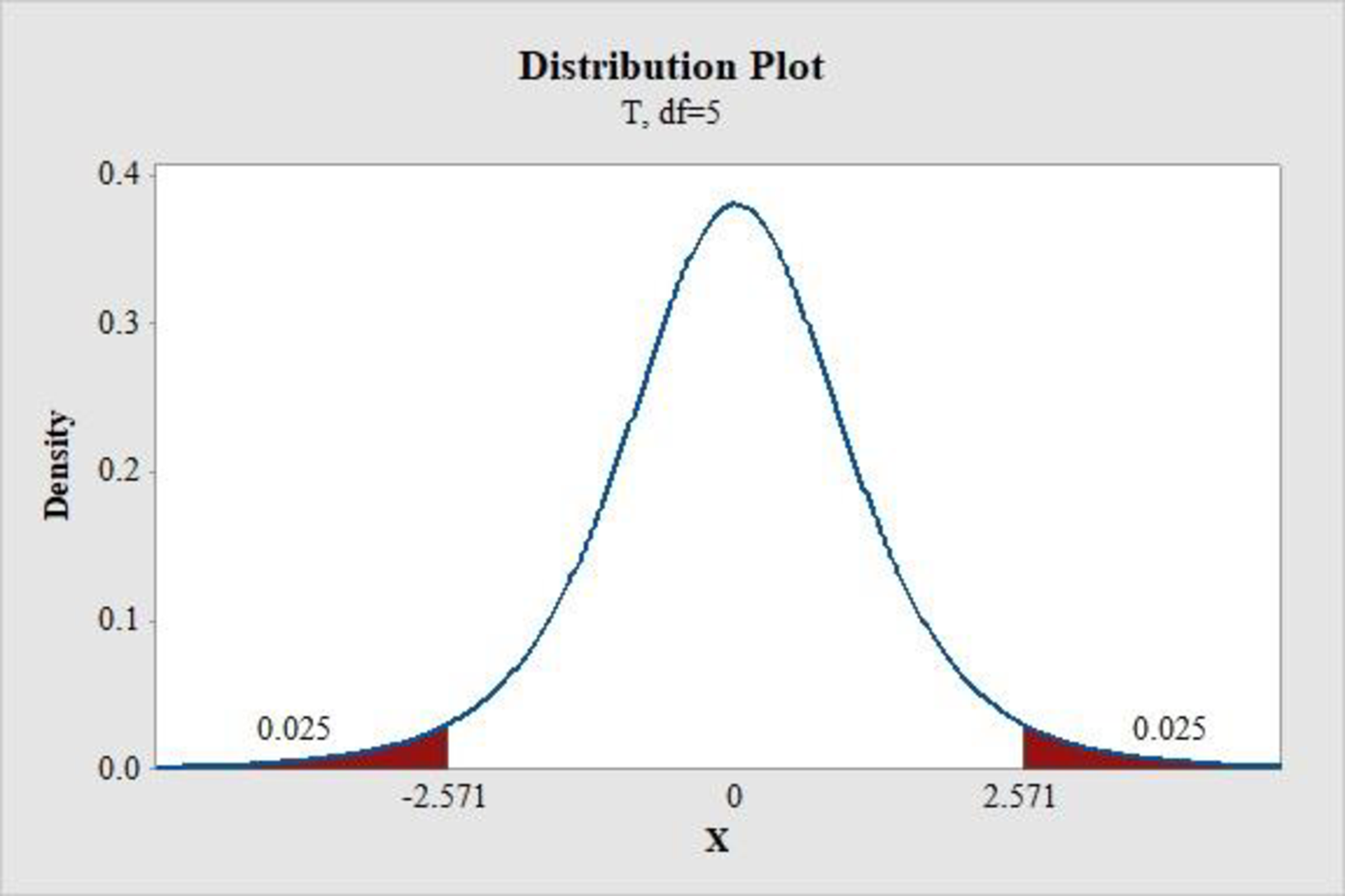
Thus, the critical value for a 95% confidence interval of ${\beta }_1$ is 2.572.

f.

To determine

Find the margin of error for a 95% confidence interval of ${\beta }_1$.

Answer to Problem 18E

The margin of error of $b_1$ is 1.944.

Explanation of Solution

Calculation:

The margin of error for a 95% confidence interval of ${\beta }_1$ is calculated using the formula:

$\text{Margin of error}=t_{\frac{\alpha }{2}}\cdot s_{b_1}$

Where,

$t_{\frac{\alpha }{2}}$ represents the two tailed critical value for a given level of significance.

$s_{b_1}$ represents the standard error of $b_1$.

Substitute $t_{\frac{\alpha }{2}}$ as 2.572 and $s_{b_1}$ as 0.756.

$\begin{array}{c}\text{Margin of error}=\left(2.571\right)\left(0.756\right)\\ =1.944\end{array}$

Thus, the margin of error of $b_1$ is 1.944.

g.

To determine

Construct the 95% confidence interval for ${\beta }_1$.

Answer to Problem 18E

The 95% confidence interval for ${\beta }_1$ is $\left(-2.00,1.88\right)$.

Explanation of Solution

Calculation:

The confidence interval for ${\beta }_1$ is calculated by using the formula:

$\text{Confidence interval}=b_1\pm t_{\frac{\alpha }{2}}\cdot s_{b_1}$

Where,

$b_1$ represents the estimated slope coefficient.

$t_{\frac{\alpha }{2}}\cdot s_{b_1}$ represents the margin of error.

$\begin{array}{c}\text{Confidence interval}=-0.063\pm \left(2.571\right)\left(0.756\right)\\ =-0.063\pm 1.944\\ =-2.00,1.88\end{array}$

Thus, the 95% confidence interval for ${\beta }_1$ is $\left(-2.00,1.88\right)$.

h.

To determine

Test the significance of ${\beta }_1$ using 5% level of significance.

Answer to Problem 18E

There is no support of evidence to conclude that there is a linear relationship between x and y at 5% level of significance.

Explanation of Solution

Calculation:

The hypotheses used for testing the significance is given below:

Null hypothesis:

$H_0:{\beta }_1=0$

That is, there is no linear relationship between x and y.

Alternate hypothesis:

$H_1:{\beta }_1\ne 0$

That is, there is a linear relationship between x and y.

Test statistic:

$t=\frac{{\widehat{\beta }}_1-{\beta }_1}{s_{b_1}}$

Where,

${\widehat{\beta }}_1$ represents the estimated slope coefficient.

${\beta }_1$ represents the hypothesized value of slope coefficient.

$s_{b_1}$ represents the standard error of slope coefficient.

Substitute ${\widehat{\beta }}_1$ as –0.063, ${\beta }_1$ as 0 and $s_{b_1}$ as 0.756.

$\begin{array}{c}t=\frac{-0.063-0}{0.756}\\ =\frac{-0.063}{0.756}\\ =0.083\end{array}$

From part e, the critical value is identified as 2.571.

Decision Rule:

Reject the null hypothesis when the test statistic value is greater than the critical value for a given level of significance. Otherwise, do not reject the null hypothesis.

Conclusion:

The test statistic value is 0.083 and the critical value is 2.571.

The test statistic value is lesser than the critical value.

That is, $0.083\left(=\text{test statistic}\right)<2.571\left(=\text{critical value}\right)$

Thus, the null hypothesis is not rejected.

Hence, there is no support of evidence to conclude that there is a linear relationship between x and y.