University Physics with Modern Physics (14th Edition)
14th Edition
ISBN: 9780321973610
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 11, Problem 11.49P
You open a restaurant and hope to entice customers by hanging out a sign (Fig. P11.49). The uniform horizontal beam supporting the sign is 1.50 m long, has a mass of 16.0 kg, and is hinged to the wall. The sign itself is uniform with a mass of 28.0 kg and overall length of 1.20 m. The two wires supporting the sign are each 32.0 cm long, are 90.0 cm apart, and are equally spaced from the middle of the sign. The cable supporting the beam is 2.00 in long. (a) What minimum tension must your cable be able to support without having your sign come crashing down? (b) What minimum vertical force must the hinge be able to support without pulling out of the wall?
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule06:46
Students have asked these similar questions
You open a restaurant and hope to entice customers by hanging out a sign (Figure 1). The uniform horizontal beam supporting the sign is 1.60 m long, has a mass of 20.0 kg , and is hinged to the wall. The sign itself is uniform with a mass of 34.0 kg and overall length of 1.20 m . The two wires supporting the sign are each 34.0 cm long, are 90.0 cm apart, and are equally spaced from the middle of the sign. The cable supporting the beam is 2.20 m long.
1. What minimum tension must your cable be able to support without having your sign come crashing down?
2. What minimum vertical force must the hinge be able to support without pulling out of the wall?
You open a restaurant and hope to entice customers by hanging out a sign (Figure 1). The uniform horizontal beam supporting the sign is 1.60 m long, has a mass of 20.0 kg , and is hinged to the wall. The sign itself is uniform with a mass of 34.0 kg and overall length of 1.20 m . The two wires supporting the sign are each 34.0 cm long, are 90.0 cm apart, and are equally spaced from the middle of the sign. The cable supporting the beam is 2.20 m long.
1. What minimum tension must your cable be able to support without having your sign come crashing down?
2. What minimum vertical force must the hinge be able to support without pulling out of the wall?
A bridge of length 50.0 m and mass 8.00 X 104 kg is supported on a smooth pier at each end as in Figure P12.39. A truck of mass 3.00 X 104 kg is located 15.0 m from one end. What are the forces on the bridge at the points of support?
Chapter 11 Solutions
University Physics with Modern Physics (14th Edition)
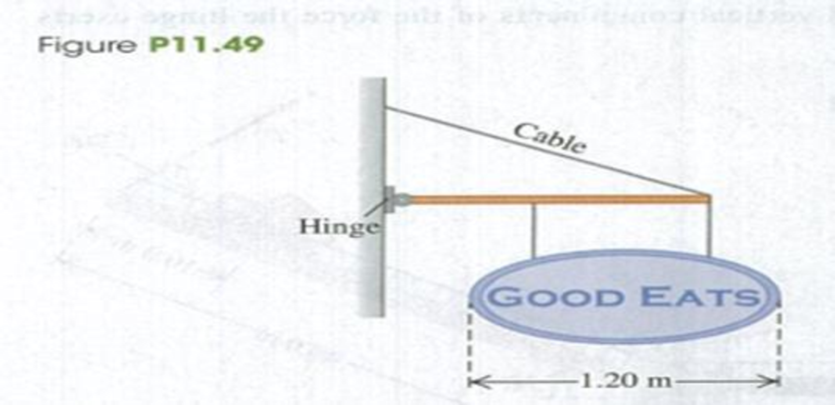
Ch. 11.1 - Which situation satisfies both the first and...Ch. 11.2 - A rock is attached to the left end of a uniform...Ch. 11.3 - A metal advertising sign (weight w) for a...Ch. 11.4 - A copper rod of cross-sectional area 0.500 cm2 and...Ch. 11.5 - While parking your car, you accidentally back into...Ch. 11 - Does a rigid object in uniform rotation about a...Ch. 11 - (a) Is it possible for an object to be in...Ch. 11 - Prob. 11.3DQCh. 11 - Does the center of gravity of a solid body always...Ch. 11 - Prob. 11.5DQ
Ch. 11 - You are balancing a wrench by suspending it at a...Ch. 11 - You can probably stand flatfooted on the floor and...Ch. 11 - Prob. 11.8DQCh. 11 - An object consists of a ball of weight W glued to...Ch. 11 - Prob. 11.10DQCh. 11 - Prob. 11.11DQCh. 11 - In pioneer days, when a Conestoga wagon was stuck...Ch. 11 - The mighty Zimbo claims to have leg muscles so...Ch. 11 - Why is it easier to hold a 10-kg dumbbell in your...Ch. 11 - Certain features of a person, such as height and...Ch. 11 - During pregnancy, women often develop back pains...Ch. 11 - Why is a tapered water glass with a narrow base...Ch. 11 - Prob. 11.18DQCh. 11 - A uniform beam is suspended horizontally and...Ch. 11 - If a metal wire has its length doubled and its...Ch. 11 - A metal wire of diameter D stretches by 0.100 mm...Ch. 11 - Prob. 11.22DQCh. 11 - The material in human bones and elephant bones is...Ch. 11 - There is a small bui appreciable amount of elastic...Ch. 11 - When rubber mounting blocks are used to absorb...Ch. 11 - A 0.120-kg. 50.0-cm-long uniform bar has a small...Ch. 11 - Prob. 11.2ECh. 11 - A uniform rod is 2.00 m long and has mass 1.80 kg....Ch. 11 - A uniform 300-N trapdoor in a floor is hinged at...Ch. 11 - Raising a Ladder. A ladder carried by a fire truck...Ch. 11 - Two people are carrying a uniform wooden board...Ch. 11 - Two people carry a heavy electric motor by placing...Ch. 11 - A 60.0-cm. uniform. 50.0-N shelf is supported...Ch. 11 - A 350-N, uniform. 1.50-m bar is suspended...Ch. 11 - A uniform ladder 5.0 m long rests against a...Ch. 11 - A diving board 3.00 m long is supported at a point...Ch. 11 - A uniform aluminum beam 9.00 m long, weighing 300...Ch. 11 - Find the tension T in each cable and the magnitude...Ch. 11 - The horizontal beam in Fig. E11.14 weighs 190 N....Ch. 11 - The boom shown in Fig. E11.15 weighs 2600 N and is...Ch. 11 - Suppose that you can lift no more than 650 N...Ch. 11 - A 9.00-m-long uniform beam is hinged to a vertical...Ch. 11 - A 15,000-N crane pivots around a friction-free...Ch. 11 - A 3.00-m-long. 190-N, uniform rod at the zoo is...Ch. 11 - A nonuniform beam 4.50 m long and weighing 1.40 kN...Ch. 11 - A Couple. Two forces equal in magnitude and...Ch. 11 - BIO A Good Workout. You are doing exercises on a...Ch. 11 - BIO Neck Muscles. A student bends her head at 40.0...Ch. 11 - BIO Biceps Muscle. A relaxed biceps muscle...Ch. 11 - A circular steel wire 2.00 m long must stretch no...Ch. 11 - Two circular rods, one steel and the other copper,...Ch. 11 - A metal rod that is 4.00 m long and 0.50 cm2 in...Ch. 11 - Stress on a Mountaineers Rope. A nylon rope used...Ch. 11 - In constructing a large mobile, an artist hangs an...Ch. 11 - A vertical, solid steel post 25 cm in diameter and...Ch. 11 - BIO Compression of Human Bone. The bulk modulus...Ch. 11 - A solid gold bar is pulled up from the hold of the...Ch. 11 - A specimen of oil having an initial volume of 600...Ch. 11 - In the Challenger Deep of the Marianas Trench, the...Ch. 11 - A copper cube measures 6.00 cm on each side. The...Ch. 11 - A square steel plate is 10.0 cm on a side and...Ch. 11 - In lab tests on a 9.25-cm cube of a certain...Ch. 11 - A brass wire is to withstand a tensile force of...Ch. 11 - In a materials testing laboratory, a metal wire...Ch. 11 - A 4.0-m-long steel wire has a cross-sectional area...Ch. 11 - CP A steel cable with cross-sectional area 3.00...Ch. 11 - A door 1.00 m wide and 2.00 m high weighs 330 N...Ch. 11 - A box of negligible mass rests at the lett end of...Ch. 11 - Sir Lancelot rides slowly out of the castle at...Ch. 11 - Mountain Climbing. Mountaineers often use a rope...Ch. 11 - A uniform, 8.0-m, 1150-kg beam is hinged to a wall...Ch. 11 - A uniform, 255.N rod that is 2.00 m long carries a...Ch. 11 - A claw hammer is used to pull a nail out of a...Ch. 11 - You open a restaurant and hope to entice customers...Ch. 11 - End A of the bar AB in Fig. P11.50 rests on a...Ch. 11 - BIO Supporting a Broken Leg. A therapist tells a...Ch. 11 - A Truck on a Drawbridge. A loaded cement mixer...Ch. 11 - BIO Leg Raises. In a simplified version of the...Ch. 11 - BIO Pumping Iron. A 72.0-kg weightlifter doing arm...Ch. 11 - Prob. 11.55PCh. 11 - You are asked to design the decorative mobile...Ch. 11 - A uniform, 7.5-m-long beam weighing 6490 N is...Ch. 11 - CP A uniform drawbridge must be held at a 37 angle...Ch. 11 - BIO Tendon-Stretching Exercises. As part of an...Ch. 11 - (a) In Fig. P11.60 a 6.00-m-loog, uniform beam is...Ch. 11 - A uniform, horizontal flagpole 5.00 m long with a...Ch. 11 - A holiday decoration consists of two shiny glass...Ch. 11 - BIO Downward-Facing Dog. The yoga exercise...Ch. 11 - A uniform metal bar that is 8.00 m long and has...Ch. 11 - A worker wants to turn over a uniform. 1250-N,...Ch. 11 - One end of a uniform meter stick is placed against...Ch. 11 - Two friends are carrying a 200-kg crate up a...Ch. 11 - BIO Forearm. In the human arm, the forearm and...Ch. 11 - BIO CALC Refer to the discussion of holding a...Ch. 11 - In a city park a nonuniform wooden beam 4.00 m...Ch. 11 - You are a summer intern for an architectural firm....Ch. 11 - You are trying to raise a bicycle wheel of mass m...Ch. 11 - The Farmyard Gate. A gate 4.00 m wide and 2.00 m...Ch. 11 - If you put a uniform block at the edge of a table,...Ch. 11 - Two uniform, 75.0-g marbles 2.00 cm in diameter...Ch. 11 - Two identical, uniform beams weighing 260 N each...Ch. 11 - An engineer is designing a conveyor system for...Ch. 11 - A weight W is supported by attaching it to a...Ch. 11 - A garage door is mounted on an overhead rail (Fig....Ch. 11 - Pyramid Guilders. Ancient pyramid builders are...Ch. 11 - CP A 12.0-kg mass, fastened to the end of an...Ch. 11 - Hookes Law for a Wire. A wire of length l0 and...Ch. 11 - A 1.05-m-long rod of negligible weight is...Ch. 11 - CP An amusement park ride consists of...Ch. 11 - CP BIO Stress on the Shin Bone. The compressive...Ch. 11 - DATA You are to use a long, thin wire to build a...Ch. 11 - Prob. 11.87PCh. 11 - DATA You are a construction engineer working on...Ch. 11 - Two ladders, 4.00 m and 3.00 m long, are hinged at...Ch. 11 - Knocking Over a Post. One end of a post weighing...Ch. 11 - An angler hangs a 4.50-kg fish from a vertical...Ch. 11 - BIO TORQUES AND TUG-OF-WAR. In a study of the...Ch. 11 - If he leans slightly farther back (increasing the...Ch. 11 - BIO TORQUES AND TUG-OF-WAR. In a study of the...Ch. 11 - BIO TORQUES AND TUG-OF-WAR. In a study of the...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Modified True/False 9. A giant bacterium that is large enough to be seen without a microscope is Selenomonas.
Microbiology with Diseases by Body System (5th Edition)
[14.110] The following mechanism has been proposed for the gas-phase reaction of chloroform (CHCI3) and chlorin...
Chemistry: The Central Science (14th Edition)
Choose the best answer to each of the following. Explain your reasoning. The reason we do not have a solar ecli...
Cosmic Perspective Fundamentals
Which compound is more easily decarboxylated?
Organic Chemistry (8th Edition)
Identify each of the following characteristics as belonging to cervical, thoracic, or lumbar vertebrae; the sac...
Human Anatomy & Physiology (2nd Edition)
How Would the experiments result charge if oxygen (O2) were induced in the spark chamber?
Biology: Life on Earth with Physiology (11th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A stepladder of negligible weight is constructed as shown in Figure P12.40, with AC = BC = = 4.00 m. A painter of mass m = 70.0 kg stands on the ladder d = 3.00 m from the bottom. Assuming the floor is frictionless, find (a) the tension in the horizontal bar DE connecting the two halves of the ladder, (b) the normal forces at A and B, and (c) the components of the reaction force at the single hinge C that the left half of the ladder exerts on the right half. Suggestion: Treat the ladder as a single object, but also treat each half of the ladder separately. Figure P12.40 Problems 40 and 41.arrow_forwardWhy is the following situation impossible? A worker in a factory pulls a cabinet across the floor using a rope as shown in Figure P12.36a. The rope make an angle = 37.0 with the floor and is tied h1 = 10.0 cm from the bottom of the cabinet. The uniform rectangular cabinet has height = 100 cm and width w = 60.0 cm, and it weighs 400 N. The cabinet slides with constant speed when a force F = 300 N is applied through the rope. The worker tires of walking backward. He fastens the rope to a point on the cabinet h2 = 65.0 cm off the floor and lays the rope over his shoulder so that he can walk forward and pull as shown in Figure P12.36b. In this way, the rope again makes an angle of = 37.0 with the horizontal and again has a tension of 300 N. Using this technique, the worker is able to slide the cabinet over a long distance on the floor without tiring. Figure P12.36 Problems 36 and 44.arrow_forwardA stepladder of negligible weight is constructed as shown in Figure P12.40, with AC = BC = . A painter of mass m stands on the ladder a distance d from the bottom. Assuming the floor is frictionless, find (a) the tension in the horizontal bar DE connecting the two halves of the ladder, (b) the normal forces at A and B, and (c) the components of the reaction force at the single hinge C that the left half of the ladder exerts on the right half. Suggestion: Treat the ladder as a single object, but also treat each half of the ladder separately. Figure P12.40 Problems 40 and 41.arrow_forward
- A uniform beam resting on two pivots has a length L = 6.00 m and mass M = 90.0 kg. The pivot under the left end exerts a normal force n1 on the beam, and the second pivot located a distance = 4.00 m from the left end exerts a normal force n2. A woman of mass m = 55.0 kg steps onto the left end of the beam and begins walking to the right as in Figure P10.28. The goal is to find the womans position when the beam begins to tip. (a) What is the appropriate analysis model for the beam before it begins to tip? (b) Sketch a force diagram for the beam, labeling the gravitational and normal forces acting on the beam and placing the woman a distance x to the right of the first pivot, which is the origin. (c) Where is the woman when the normal force n1 is the greatest? (d) What is n1 when the beam is about to tip? (e) Use Equation 10.27 to find the value of n2 when the beam is about to tip. (f) Using the result of part (d) and Equation 10.28, with torques computed around the second pivot, find the womans position x when the beam is about to tip. (g) Check the answer to part (e) by computing torques around the first pivot point. Figure P10.28arrow_forwardFigure P12.38 shows a light truss formed from three struts lying in a plane and joined by three smooth hinge pins at their ends. The truss supports a downward force of F=1000N applied at the point B. The truss has negligible weight. The piers at A and C are smooth. (a) Given 1 = 30.0 and 2 = 45.0, find nA and nC. (b) One can show that the force any strut exerts on a pin must be directed along the length of the strut as a force of tension or compression. Use that fact to identify the directions of the forces that the struts exert on the pins joining them. Find the force of tension or of compression in each of the three bars. Figure P12.38arrow_forwardA 500-N uniform rectangular sign 4.00 m wide and 3.00 m high is suspended from a horizontal, 6.00-m-long, uniform. 100-N rod as indicated in Figure P12.47. The left end of the rod is supported by a hinge, and the right end is supported by a thin cable making a 30.0 angle with the vertical. (a) Find the tension T in the cable. (b) Find the horizontal and vertical components of force exerted on the left end of the rod by the hinge. Figure P12.47arrow_forward
- Consider a nanotube with a Youngs modulus of 2.130 1012 N/m2 that experiences a tensile stress of 5.3 1010 N/m2. Steel has a Youngs modulus of about 2.000 1011 Pa. How much stress would cause a piece of steel to experience the same strain as the nanotube?arrow_forwardWhen a circus performer performing on the rings executes the iron cross, he maintains the position at rest shown in Figure P12.37a. In this maneuver, the gymnasts feet (not shown) are off the floor. The primary muscles involved in supporting this position are the latissimus dorsi (lats) and the pectoralis major (pecs). One of the rings exerts an upward force Fk on a hand as show n in Figure P12.37b. The force Fs, is exerted by the shoulder joint on the arm. The latissimus dorsi and pectoralis major muscles exert a total force Fm on the arm. (a) Using the information in the figure, find the magnitude of the force Fm for an athlete of weight 750 N. (b) Suppose a performer in training cannot perform the iron cross but can hold a position similar to the figure in which the arms make a 45 angle with the horizontal rather than being horizontal. Why is this position easier for the performer? Figure P12.37arrow_forwardWhy is the following situation impossible? A uniform beam of mass mk = 3.00 kg and length = 1.00 m supports blocks with masses m1 = 5.00 kg and m2 = 15.0 kg at two positions as shown in Figure P12.2. The beam rests on two triangular blocks, with point P a distance d = 0.300 m to the right of the center of gravity of the beam. The position of the object of mass m2 is adjusted along the length of the beam until the normal force on the beam at O is zero. Figure P12.2arrow_forward
- Problems 33 and 34 are paired. One end of a uniform beam that weighs 2.80 102 N is attached to a wall with a hinge pin. The other end is supported by a cable making the angles shown in Figure P14.33. Find the tension in the cable. FIGURE P14.33 Problems 33 and 34.arrow_forwardNO 4. End A of the bar AB Figure P11.53 in Fig. P11.53 rests on a fric- tionless horizontal surface, and В end B is hinged. A horizontal force F of magnitude 160 N is 5.00 m 4.00 m exerted on end A. You can ignore the weight of the bar. A What are the horizontal and vertical components of the force exerted by the bar on the hinge at B? Figure P11.54arrow_forwardThe left-hand end of a 2.50 kg rod with a 2.00 m length is attached to a vertical wall by a hinge. A 3.00 kg object is suspended from the rod at a point 1.80 m from the hinge. The rod is held in a horizontal position by a light wire that runs from the right-hand end of the rod to the wall. The wire makes a 35.0degree angle with the rod. (a) What is the tension on the wire? (b) What is the vertical force on the hinge?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Static Equilibrium: concept; Author: Jennifer Cash;https://www.youtube.com/watch?v=0BIgFKVnlBU;License: Standard YouTube License, CC-BY