Precalculus: Mathematics for Calculus - 6th Edition
6th Edition
ISBN: 9780840068071
Author: Stewart, James, Redlin, Lothar, Watson, Saleem
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 10.6, Problem 63E
a.
To determine
The coordinates of the vertices of the surrounding rectangle and calculate the area.
a.
Expert Solution
Answer to Problem 63E
The area of the rectangle is R=(a3−a1).(b2−b1)=a3b2+a1b1−a1b1−a3b2
Explanation of Solution
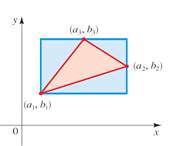
First finding the coordinates by seeing how the rectangle is formed by the lines x=a1,x=a3,y=b1,y=b2.
So, the line equation by noting he coordinates of the points on them. So, the four vertices of the rectangle are given by,
(a1,b1),(a1,b2),(a3,b1),(a3,b2)
The area of the rectangle id then simply,
R=(a3−a1).(b2−b1)=a3b2+a1b1−a1b1−a3b2
Conclusion:
Hence, the area of the rectangle is R=(a3−a1).(b2−b1)=a3b2+a1b1−a1b1−a3b2
b.
To determine
The area of the red tringle by subtracting the area of the three blue triangles from the area of the rectangle.
b.
Expert Solution
Answer to Problem 63E
The area of the red tringle by subtracting the area of the three blue triangles from the area of the rectangle is 12(a1b3−a3b1−a2b3+a3b2+a1b2+a2b1)
Explanation of Solution
Calculation:
B=12(a3−a1|(b1−b3)+12(a2−a3)(b3−b2)+12(a2−a1)(b2−b1))B=12(a1b1+a3b3−a1b3−a3b1−a2b2−a3b3+a2b3+a3b2+a2b2+a1b1−a1b1−a2b1)B=12(−a1b3+b1a3+a2b3+a3b2−a1b2−a2b1)
So, the area A of the red triangle is then,
A=R−BA=12(a1b3−a3b1−a2b3+a3b2+a1b2+a2b1)
Conclusion:
Hence, the area is 12(a1b3−a3b1−a2b3+a3b2+a1b2+a2b1) .
c.
To determine
By using 12(a1b3−a3b1−a2b3+a3b2+a1b2+a2b1) show that the area of the red triangle is given by
area = ±12|a1b11a2b21a3b31|
c.
Expert Solution
Answer to Problem 63E
Showed that the area of the rectangle is giving by the area = ±12|a1b11a2b21a3b31|
Explanation of Solution
Given:
area = ±12|a1b11a2b21a3b31|
Calculation:
First expand the determinant given the 3rd column,
|a1b11a2b21a3b31|=|a2b2a3b3|−|a1b1a3b3|+|a1b1a2b2|=(a2b3−b2a3)−(a1b3−b1a3)+(a1b2−b1a2)=−a1b3+a3b1+a2b3−a3b2+a1b2−a2b1
The sign of the difference arises from the loss of generality because the ordering picked for a1,a2,a3 and b1,b2,b3 is specific as given in the diagram in the book. So hence write the determinant in an absolute value to fix this and the final result is the proof as,
A=10abs(|a1b11a2b21a3b31|)
Conclusion:
Hence, area of the rectangle is giving by the area = ±12|a1b11a2b21a3b31| is proved.
Chapter 10 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
Ch. 10.1 - The system of equations {2x+3y=75xy=9 is a system...Ch. 10.1 - Prob. 2ECh. 10.1 - A system of two linear equations in two variables...Ch. 10.1 - The following is a system of two linear equations...Ch. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10E
Ch. 10.1 - Prob. 11ECh. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Value of Coins A man has 14 coins in his pocket,...Ch. 10.1 - Admission Fees The admission fee at an amusement...Ch. 10.1 - Gas Station A gas station sells regular gas for...Ch. 10.1 - Fruit Stand A fruit stand sells two varieties of...Ch. 10.1 - Airplane Speed A man flies a small airplane from...Ch. 10.1 - Boat Speed A boat on a river travels downstream...Ch. 10.1 - Nutrition A researcher performs an experiment to...Ch. 10.1 - Coffee Blends A customer in a coffee shop...Ch. 10.1 - Mixture Problem A chemist has two large containers...Ch. 10.1 - Mixture Problem A biologist has two brine...Ch. 10.1 - Investments A woman invests a total of 20,000 in...Ch. 10.1 - Investments A man invests his savings in two...Ch. 10.1 - Prob. 71ECh. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Area of a Triangle Find the area of the triangle...Ch. 10.1 - Prob. 75ECh. 10.2 - These exercises refer to the following system:...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Gas Station A gas station sells three types of...Ch. 10.2 - Nutrition A biologist is performing an experiment...Ch. 10.2 - Diet Program Nicole started a new diet that...Ch. 10.2 - Juice Blends The Juice Company offers three kinds...Ch. 10.2 - Appliance Manufacturing Kitchen Korner produces...Ch. 10.2 - Stock Portfolio An investor owns three stocks: A,...Ch. 10.2 - Electricity By using Kirchhoffs Laws, it can be...Ch. 10.2 - Prob. 47ECh. 10.3 - If a system of linear equations has infinitely...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Nutrition A doctor recommends that a patient take...Ch. 10.3 - Mixtures A chemist has three acid solutions at...Ch. 10.3 - Distance, Speed, and Time Amanda, Bryce, and Corey...Ch. 10.3 - Classroom Use A small school has 100 students who...Ch. 10.3 - Manufacturing Furniture A furniture factory makes...Ch. 10.3 - Traffic Flow A section of a citys street network...Ch. 10.3 - Prob. 61ECh. 10.4 - We can add (or subtract) two matrices only if they...Ch. 10.4 - (a) We can multiply two matrices only if the...Ch. 10.4 - Prob. 3ECh. 10.4 - Fill in the missing entries in the product matrix....Ch. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Fast-Food Sales A small fast-food chain with...Ch. 10.4 - Prob. 46ECh. 10.4 - Canning Tomato Products Jaeger Foods produces...Ch. 10.4 - Produce Sales A farmers three children, Amy, Beth,...Ch. 10.4 - Digital Images A four-level gray scale is shown...Ch. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.5 - (a) The matrix I=[1001] is called an __________...Ch. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Nutrition A nutritionist is studying the effects...Ch. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.6 - True or false? det(A) is defined only for a square...Ch. 10.6 - Prob. 2ECh. 10.6 - True or false? If det(A) = 0, then A is not...Ch. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Prob. 55ECh. 10.6 - Prob. 56ECh. 10.6 - Prob. 57ECh. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - The Arch of a Bridge The opening of a railway...Ch. 10.6 - A Triangular Plot of Land An outdoors club is...Ch. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Prob. 66ECh. 10.6 - Prob. 67ECh. 10.7 - For each rational function r, choose from (i)(iv)...Ch. 10.7 - Prob. 2ECh. 10.7 - Prob. 3ECh. 10.7 - Prob. 4ECh. 10.7 - Prob. 5ECh. 10.7 - Prob. 6ECh. 10.7 - Prob. 7ECh. 10.7 - Prob. 8ECh. 10.7 - Prob. 9ECh. 10.7 - Prob. 10ECh. 10.7 - Prob. 11ECh. 10.7 - Prob. 12ECh. 10.7 - Prob. 13ECh. 10.7 - Prob. 14ECh. 10.7 - Prob. 15ECh. 10.7 - Prob. 16ECh. 10.7 - Prob. 17ECh. 10.7 - Prob. 18ECh. 10.7 - Prob. 19ECh. 10.7 - Prob. 20ECh. 10.7 - Prob. 21ECh. 10.7 - Prob. 22ECh. 10.7 - Prob. 23ECh. 10.7 - Prob. 24ECh. 10.7 - Prob. 25ECh. 10.7 - Prob. 26ECh. 10.7 - Prob. 27ECh. 10.7 - Prob. 28ECh. 10.7 - Prob. 29ECh. 10.7 - Prob. 30ECh. 10.7 - Prob. 31ECh. 10.7 - Prob. 32ECh. 10.7 - Prob. 33ECh. 10.7 - Prob. 34ECh. 10.7 - Prob. 35ECh. 10.7 - Prob. 36ECh. 10.7 - Prob. 37ECh. 10.7 - Prob. 38ECh. 10.7 - Prob. 39ECh. 10.7 - Prob. 40ECh. 10.7 - Prob. 41ECh. 10.7 - Prob. 42ECh. 10.7 - Prob. 43ECh. 10.7 - Prob. 44ECh. 10.7 - Prob. 45ECh. 10.7 - Prob. 46ECh. 10.7 - Prob. 47ECh. 10.7 - Prob. 48ECh. 10.8 - The system of equations {2yx2=0yx=4 is graphed...Ch. 10.8 - Prob. 2ECh. 10.8 - Prob. 3ECh. 10.8 - Prob. 4ECh. 10.8 - Prob. 5ECh. 10.8 - Prob. 6ECh. 10.8 - Prob. 7ECh. 10.8 - Prob. 8ECh. 10.8 - Prob. 9ECh. 10.8 - Prob. 10ECh. 10.8 - Prob. 11ECh. 10.8 - Prob. 12ECh. 10.8 - Prob. 13ECh. 10.8 - Prob. 14ECh. 10.8 - Prob. 15ECh. 10.8 - Prob. 16ECh. 10.8 - Prob. 17ECh. 10.8 - Prob. 18ECh. 10.8 - Prob. 19ECh. 10.8 - Prob. 20ECh. 10.8 - Prob. 21ECh. 10.8 - Prob. 22ECh. 10.8 - Prob. 23ECh. 10.8 - Prob. 24ECh. 10.8 - Prob. 25ECh. 10.8 - Prob. 26ECh. 10.8 - Prob. 27ECh. 10.8 - Prob. 28ECh. 10.8 - Prob. 29ECh. 10.8 - Prob. 30ECh. 10.8 - Prob. 31ECh. 10.8 - Prob. 32ECh. 10.8 - Prob. 33ECh. 10.8 - Prob. 34ECh. 10.8 - Prob. 35ECh. 10.8 - Prob. 36ECh. 10.8 - Prob. 37ECh. 10.8 - Prob. 38ECh. 10.8 - Prob. 39ECh. 10.8 - Prob. 40ECh. 10.8 - Dimensions of a Rectangle A rectangle has an area...Ch. 10.8 - Legs of a Right Triangle A right triangle has an...Ch. 10.8 - Dimensions of a Rectangle The perimeter of a...Ch. 10.8 - Dimensions of a Rectangle A circular piece of...Ch. 10.8 - Flight of a Rocket A hill is inclined so that its...Ch. 10.8 - Making a Stovepipe A rectangular piece of sheet...Ch. 10.8 - Global Positioning System (GPS) The Global...Ch. 10.8 - Prob. 48ECh. 10.8 - Prob. 49ECh. 10.9 - To graph an inequality, we first graph the...Ch. 10.9 - Prob. 2ECh. 10.9 - Prob. 3ECh. 10.9 - Prob. 4ECh. 10.9 - Prob. 5ECh. 10.9 - Prob. 6ECh. 10.9 - Prob. 7ECh. 10.9 - Prob. 8ECh. 10.9 - Prob. 9ECh. 10.9 - Prob. 10ECh. 10.9 - Prob. 11ECh. 10.9 - Prob. 12ECh. 10.9 - Prob. 13ECh. 10.9 - Prob. 14ECh. 10.9 - Prob. 15ECh. 10.9 - Prob. 16ECh. 10.9 - Prob. 17ECh. 10.9 - Prob. 18ECh. 10.9 - Prob. 19ECh. 10.9 - Prob. 20ECh. 10.9 - Prob. 21ECh. 10.9 - Prob. 22ECh. 10.9 - Prob. 23ECh. 10.9 - Prob. 24ECh. 10.9 - Prob. 25ECh. 10.9 - Prob. 26ECh. 10.9 - Prob. 27ECh. 10.9 - Prob. 28ECh. 10.9 - Prob. 29ECh. 10.9 - Prob. 30ECh. 10.9 - Prob. 31ECh. 10.9 - Prob. 32ECh. 10.9 - Prob. 33ECh. 10.9 - Prob. 34ECh. 10.9 - Prob. 35ECh. 10.9 - Prob. 36ECh. 10.9 - Prob. 37ECh. 10.9 - Prob. 38ECh. 10.9 - Prob. 39ECh. 10.9 - Prob. 40ECh. 10.9 - Prob. 41ECh. 10.9 - Prob. 42ECh. 10.9 - Prob. 43ECh. 10.9 - Prob. 44ECh. 10.9 - Prob. 45ECh. 10.9 - Prob. 46ECh. 10.9 - Prob. 47ECh. 10.9 - Prob. 48ECh. 10.9 - Prob. 49ECh. 10.9 - Prob. 50ECh. 10.9 - Prob. 51ECh. 10.9 - Prob. 52ECh. 10.9 - Coffee Blends A coffee merchant sells two...Ch. 10.9 - Nutrition A cat food manufacturer uses fish and...Ch. 10.9 - Prob. 55ECh. 10 - Prob. 1RCCCh. 10 - Prob. 2RCCCh. 10 - Prob. 3RCCCh. 10 - Prob. 4RCCCh. 10 - Prob. 5RCCCh. 10 - Prob. 6RCCCh. 10 - Prob. 7RCCCh. 10 - Prob. 8RCCCh. 10 - Prob. 9RCCCh. 10 - Prob. 10RCCCh. 10 - Prob. 11RCCCh. 10 - Prob. 12RCCCh. 10 - Prob. 13RCCCh. 10 - Prob. 14RCCCh. 10 - Prob. 15RCCCh. 10 - Prob. 16RCCCh. 10 - Prob. 17RCCCh. 10 - Prob. 18RCCCh. 10 - Prob. 19RCCCh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Prob. 97RECh. 10 - Prob. 98RECh. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 1TCh. 10 - Prob. 2TCh. 10 - Prob. 3TCh. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - Prob. 6TCh. 10 - Prob. 7TCh. 10 - Anne, Barry, and Cathy enter a coffee shop. Anne...Ch. 10 - Prob. 9TCh. 10 - Prob. 10TCh. 10 - Only one of the following matrices has an inverse....Ch. 10 - Prob. 12TCh. 10 - Prob. 13TCh. 10 - Prob. 14TCh. 10 - Find the maximum and minimum values of the given...Ch. 10 - Prob. 2PCh. 10 - Prob. 3PCh. 10 - Find the maximum and minimum value of the given...Ch. 10 - Making Furniture A furniture manufacturer makes...Ch. 10 - A Housing Development A housing contractor has...Ch. 10 - Hauling Fruit A trucker hauls citrus fruit from...Ch. 10 - Manufacturing Calculators A manufacturer of...Ch. 10 - Shipping Televisions An electronics discount chain...Ch. 10 - Prob. 10PCh. 10 - Packaging Nuts A confectioner sells two types of...Ch. 10 - Feeding Lab Rabbits A biologist wishes to feed...Ch. 10 - Investing in Bonds A woman wishes to invest 12,000...Ch. 10 - Prob. 14PCh. 10 - Business Strategy A small software company...Ch. 10 - Feasible Region All parts of this problem refer to...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Math Test 3 3 x³+y³ = Ꭹ = 9 2 2 x²+y² = 5 x+y=?arrow_forwardFor each of the following series, determine whether the absolute convergence series test determines absolute convergence or fails. For the ¿th series, if the test is inconclusive then let Mi = 4, while if the test determines absolute convergence let Mi 1 : 2: ∞ Σ(−1)"+¹ sin(2n); n=1 Σ n=1 Σ ((−1)”. COS n² 3+2n4 3: (+ 4: 5 : n=1 ∞ n 2+5n3 ПП n² 2 5+2n3 пп n² Σ(+)+ n=1 ∞ n=1 COS 4 2 3+8n3 П ηπ n- (−1)+1 sin (+727) 5 + 2m³ 4 = 8. Then the value of cos(M₁) + cos(2M2) + cos(3M3) + sin(2M) + sin(M5) is -0.027 -0.621 -1.794 -1.132 -1.498 -4.355 -2.000 2.716arrow_forwardi need help with this question i tried by myself and so i am uploadding the question to be quided with step by step solution and please do not use chat gpt i am trying to learn thank you.arrow_forward
- i need help with this question i tried by myself and so i am uploadding the question to be quided with step by step solution and please do not use chat gpt i am trying to learn thank you.arrow_forward1. 3 2 fx=14x²-15x²-9x- 2arrow_forwardNo it is not a graded assignment, its a review question but i only have the final answer not the working or explanationarrow_forward
- Class, the class silues, and the class notes, whether the series does alternate and the absolute values of the terms decrease), and if the test does apply, determine whether the series converges or diverges. For the ith series, if the test does not apply the let Mi = 2, while if the test determines divergence then M¿ = 4, and if it determines convergence then M¿ = 8. 1: 2: 3 : 4: 5 : ∞ n=1 ∞ (−1)n+1. Σ(-1) +1 n=1 ∞ п 3m² +2 Σ(-1)+1 sin(2n). n=1 ∞ 2n² + 2n +3 4n2 +6 1 e-n + n² 3n23n+1 9n² +3 In(n + 1) 2n+1 Σ(-1) +1 n=1 ∞ Σ(-1)". n=1 Then the value of cos(M₁) + cos(2M2) + cos(3M3) + sin(2M4) + sin(M5) is 1.715 0.902 0.930 -1.647 -0.057 ● 2.013 1.141 4.274arrow_forward3. FCX14) = x²+3xx-y3 +.arrow_forwardA cylindrical chemical storage tank with a capacity of 950m3 is going to be constructed in a warehouse that is 11m by 14m with a height of 10m. The specifications call for the case to be made of sheet metal that costs $90/m2, the top to be made from sheet metal that costs $45/m2 and the wall to be made of sheet metal that costs $80/m2. If you want to minimize the cost to make the storage house, how much would you end up spending to build the tank?arrow_forward
- Calculate the max value of the directional derivatearrow_forwardCalculus III May I please have the example, definition semicolons, and all blanks completed and solved? Thank you so much,arrow_forwardA company estimates that the revenue (in dollars) from the sale of x doghouses is given by R(x) = 12,000 In (0.02x+1). Use the differential to approximate the change in revenue from the sale of one more doghouse if 80 doghouses have already been sold. The revenue will increase by $ if one more doghouse is made. (Round to the nearest cent as needed.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
An Introduction to Area | Teaching Maths | EasyTeaching; Author: EasyTeaching;https://www.youtube.com/watch?v=_uKKl8R1xBM;License: Standard YouTube License, CC-BY
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=JnLDmw3bbuw;License: Standard YouTube License, CC-BY