
Concept explainers
In Problems 1-4, find all critical points and determine whether they are relative
y=−x2
To calculate: The critical values, relative maxima, relative minima, or horizontal points of inflection of the function y=−x2 by using the derivative.
Answer to Problem 1RE
Solution:
The critical value(s) are x=0, the relative maxima is x=(0,0), the relative minima is not there and the horizontal point of inflection is not there.
Explanation of Solution
Given Information:
The provided equation is y=−x2.
Formula Used:
The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.
This, in an interval between two critical values, the sign of the derivative at any value in the interval will be the sign of the derivative at all values in the interval.
As per the First Derivative Test,
The first derivative of the function is evaluated. The first derivative is made equal to zero in order to get the critical points.
The values of the critical values are kept inside the original function which gives the critical points. The intervals of the values of x are then evaluated for the relative maximum and minimum.
Calculation:
Consider the provided equation y=−x2,
The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.
Hence, there will no change in the values of critical values as in the derivative graph.
Take out the first derivative of the equation by the power rule,
y′=−2x
Put the value of y′=0,
y′=−2x=0=x=0
Hence, the values of x are x=0.
Evaluate the values of the original functions with the critical values:
Put x=0 in the equation y=−x2,
y=−(0)2=0
Hence, x=(0,0) is a critical point.
The relative maximum can be evaluated as follows by two ways, it can be understood as reaching a peak after increasing, and then going for a downfall.
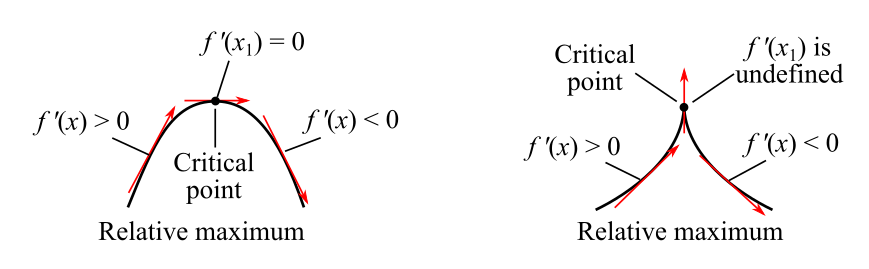
It can be observed that there is x=(0,0) as relative maxima.
The relative minimum can be evaluated as follows by two ways, it can be understood as reaching a peak after decreasing, and then going upward.
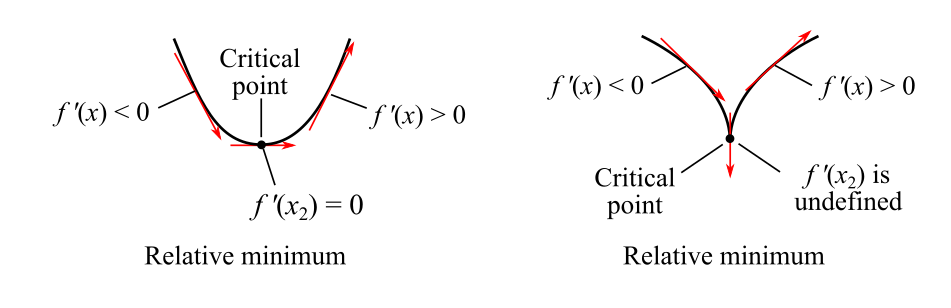
It can be observed that there is no relative minima.
If the first derivative of f is 0 at x0 but does not change from positive to negative or from negative to positive as x passes through x0, then the critical point at x0 is neither a relative maximum nor a relative minimum.
In this case, it is said that f has a horizontal point of inflection.
The horizontal point of inflection is not there.
Want to see more full solutions like this?
Chapter 10 Solutions
Mathematical Applications for the Management, Life, and Social Sciences
- A population of deer in Pierce County currently has 1875 deer, but due to urban development, the population is decreasing at a rate of 1.1% a year. a) Assuming this growth rate continues, find the formula for a function f(t) describing this population. b) In how many years will the population reach 1300? Do the problems on your own paper, show all your work, and submit your scanned work below. Choose File No file chosenarrow_forward● Question 7 Solve the equation. log2(3m - 5) = log2(m +8) m n = Question 8arrow_forwardQuestion 4 If log2(6x+3).= 4, then x = You may enter the exact value or round to 4 decimal places.arrow_forward
- Question 8 Find the domain of y = log(62x). The domain is: Question 9arrow_forwardQuestion 3 Rewrite 4 = log₂(16) in exponential form. Question 4 症 If log, (6x+3)= 4, then rarrow_forwardQuestion 6 Find the solution of the exponential equation 2t 100(1.07) 2 = 500,000 in terms of logarithms, or correct to four decimal places. t=arrow_forward
- Question 6 Find the solution of the exponential equation 100(1.07)² = 500, 000 in terms of logarithms, or correct to four decimal places. t = Question 7 Solve the equation.arrow_forwardI need help on 10arrow_forward|x6|= 5 The distance between x and is spaces on the number line, in either direction. Next Partarrow_forward
- 6 pts 1 Details 3 Find a formula for the exponential function passing through the points -3, and (3,375) 125 f(x) = Question 3arrow_forward18. Let X be normally distributed with mean μ = 2,500 and stan- dard deviation σ = 800. a. Find x such that P(X ≤ x) = 0.9382. b. Find x such that P(X>x) = 0.025. ة نفـة C. Find x such that P(2500arrow_forward17. Let X be normally distributed with mean μ = 2.5 and standard deviation σ = 2. a. Find P(X> 7.6). b. Find P(7.4≤x≤ 10.6). 21 C. Find x such that P(X>x) = 0.025. d. Find x such that P(X ≤x≤2.5)= 0.4943. and stan-arrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill




